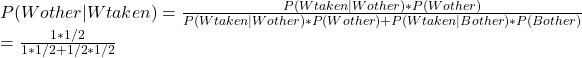Jensen’s Inequality and Banking Collapse

Let’s apply Jensen’s Inequality to the housing market. It concerns default rates on housing loans with the housing prices. When the housing prices are high, the defaults reduce; when the prices are lower, defaults increase but not in the same magnitude. Here is a fictitious plot of % of bank profit vs % change in housing price.

A 7% increase in house price increases the bank’s profit by about 7%, whereas an equivalent decrease in price leads to about a 25% drop in profit!

Jensen’s Inequality and Banking Collapse Read More »

Jensen’s Inequality

Before analysing inequality, let’s develop an intuition. Suppose the profit from sales of an object moves the following way with the price. 

The price can be 2, 3, or 4 in a given year with equal probabilities. What is the average profit?

The mathematical function that presents the above behaviour is x3 + 5. Suppose the price values (x) 2, 3, and 4 can occur equally likely. This means the average price value is (2+3+4)/3 = 3. The profit at x = 3 is 33+5 = 32. 

Let’s estimate the profit at each x value and then take the average.
at x = 2, profit = 23+5 = 13
at x = 3, profit = 33+5 = 32
at x = 4, profit = 43+5 = 69
Average is (13+32+69)/3 = 38

This is Jensen’s inequality, which says that the average (expected values) of inputs do not lead to average output if the function is non-linear. Depending on the shape of the non-linearity, it can under-estimate or over-estimate. 

Jensen’s Inequality Read More »

Binomial Aircraft

An aircraft has 200 seats. The airline knows that, on average, 5% of the people who have purchased the ticket don’t show up. What is the maximum number of tickets they can sell to manage the probability that more than 200 passengers will show up at 10%?

The number of people who do not show up (X) will follow a binomial distribution with a probability of success of 5%, X ~ Bin(200+X, 0.05). Since X is unknown, we first use the qbinom function on 200 to get an approximate solution.  

qbinom(0.1, 200, prob = 0.05, lower.tail = TRUE)
 6

Now, we use 200+6 in the equation. 

qbinom(0.1, 206, prob = 0.05, lower.tail = TRUE)
6

Binomial Aircraft Read More »

Integrating Circle for Pi

We have seen how the constant pi is estimated as a fraction of randomly ‘hitting darts’ on a circle inscribed inside a square. Here, we see how the same is done by numerically integrating a unit circle between -1 and 1.

The first part is to create the functions for the circle. 

f <- function(x)  sqrt(1-x^2)
f1 <- function(x)  -sqrt(1-x^2)

You can check it by plotting the functions using the R command ‘curve’ and shading the area using the ‘shade’ function from the library, ‘DescTools’.

min <- -1
max <- 1
par(bg = "white", pty = "s")
curve(f, from = min, to = max, ylim = c(-1,1))
curve(f1, from = min, to = max, add = TRUE)

Shade(f, breaks = c(min,max), col = "darkgreen", density = 20)
Shade(f1, breaks = c(min,max), col = "darkgreen", density = 20)

Evaluate the function between the limits to get the area. 

points <- seq(min, max, by = 0.000001)
(max-min)*mean(f(points)) - (max-min)*mean(f1(points))
3.141591

Another example is the area of the normal distribution between -1.96 and +1.96 for the well-known 95% confidence interval. 

f <- function(x)  dnorm(x)
curve(f, from = -5, to = 5)

min <- -1.96
max <- 1.96
Shade(f, breaks = c(min, max), col = "darkgreen", density = 20)

points <- seq(min, max, by = 0.00001)
(max-min)*mean(f(points))
0.9500024

Integrating Circle for Pi Read More »

The Poisson Cars and Binomial Hires

A car hire firm typically receives an average of 3 hiring requests per day. What is the probability it gets at most two hiring requests for exactly 3 days a week?

The first part of the problem (getting at most 2 requests in a day) can be solved using the Poisson probability model. It involves a random variable, X, and it takes positive values. All we know is an expected value (average value), lambda. The probability is expressed as:

P(X = s) = \frac{e^{-\lambda}\lambda^s}{s!}

Now, substitute lambda = 3 and s for at most 2 requests, i.e., the chance of 0 requests + 1 request + 2 requests.

P(X \le 2) = \frac{e^{-3} 3^2}{2!} + \frac{e^{-3} 3^1}{1!} + \frac{e^{-3} 3^0}{0!} \\ \\ = \frac{9}{2}e^{-3} + 3e^{-3} + e^{-3} = 0.423

This can be easily estimated using the R code:

ppois(2, 3, lower.tail = TRUE)

This is the daily probability for at most 2 car hire requests. For estimating the probability of 3 exact such days in a week, we use the binomial model.

P(X = 3) = _3C_7 * p^3 (1-p)^{7-3} \\ \\ P(X = 3) = _3C_7 * 0.423^3 (1-0.423)^{4} = 0.294

Or the R code. 

dbinom(3, 7, prob = ppois(2, 3, lower.tail = TRUE))

The Poisson Cars and Binomial Hires Read More »

Law of Truly Large Numbers

In their paper ‘Methods for Studying Coincidences, ‘ Diaconis and Mosteller propose the law of truly large numbers, which states that almost any outrageous event is bound to occur with a large enough number of independent samples! 

Imagine an event that happens with a probability of 0.1% or 0.001. Therefore, the chance that it doesn’t happen is 0.999. If you carry out 100 independent trials, the probability of this not occurring is 0.999100 = 0.90.  In other words, there is a 1-0.9 = 0.1 or 10% chance of occurrence. The following is the plot of this from 1 to 10,000 trials.

You can see that beyond, say, 5000 independent trials, this rare event is sure to occur at least once.   

Law of Truly Large Numbers Read More »

Confidence Interval vs Credible Interval

Confidence interval is a frequentist’s way of communicating the range of values within which the actual (population) parameter sits. A confidence interval of 90% implies that if you do 20 random samples from the same target population and with the same sample size, 18 of the confidence intervals cover the true population mean. This is the frequentist’s view, and the parameter is fixed. 

On the other hand, the Bayesian does not have a concept of a fixed parameter and is happy to accept it as an unknown quantity. Instead, she gives a probability distribution to the expected outcome. The range of values (the interval) of the probability distribution (plausibility) is the credibility interval. In a 90% credible interval, the portion of the (posterior) distributions between the two intervals will cover 90% of the area.

For example, in the following posterior distribution, there is a 90% plausibility that the parameter lies between 0.9 and 11.2; the shaded area = 0.9.

Confidence Interval vs Credible Interval Read More »

Lewis Carroll’s Pillow Problem

Here is one of the Lewis Carroll’s Pillow Problems (problem # 5):

A bag contains a counter, known to be either white or black. A white counter is put in, the bag is shaken, and a counter is drawn out, which proves to be white. What is now the chance of drawing a white counter?

We will use Bayes’ theory to get the required probability.

\\ P(W other|W taken) = \frac{P(W taken|W other) * P(W other)}{P(W taken|W other) * P(W other) + P(W taken|B other) * P(B other)} \\ = \frac{1*1/2}{1*1/2 + 1/2*1/2}

= 1/2/[1/2+1/4] = 2/3 = 0.66

Lewis Carroll’s Pillow Problem Read More »

Bayesian Persuasion

Persuasion is the act of a person (a.k.a. the sender) to convince another (the receiver) to decide in favour of the sender. Suppose the receiver is a judge and the sender is the prosecutor. The prosecutor aims to make the judge convict 100% of the defendants. But the judge knows that only a third of the defendants are guilty. Can the prosecutor persuade the judge to get more than 33% of the decisions in her favour? If the judge is rational, what should be the prosecutor’s strategy?  

Suppose the prosecutor has the research report and the knowledge about the truth. She can follow the following three strategies.

Strategy 1: Always guilty

The prosecutor reports that the defendant is guilty 100% of the time, irrespective of what happened. In this process, the prosecutor loses credibility, and the judge resorts to the prior probability of a person being guilty, which is 33%. The result? Always acquit the defendant. The prosecutor’s incentive is 0. 

Strategy 2: Full information

The prosecutor keeps it simple – report what the research finds. It makes her credibility 100%, and the judge will follow the report, convicting 33% and acquiring 66%. The prosecutor’s incentive is 0.33. 

Strategy 3: Noisy information

Here, when the research suggests the defendant is innocent, report that the defendant is guilty slightly less than 50% of the time and innocent the rest of the time. Let this fraction be 3/7 for guilty and 4/7 for innocent. 

From the judge’s perspective, if she sees an ‘innocent’ report from the prosecutor, she will acquit the defendant. The proportion of time this will happen is (2/3) x (4/7) or 40%. Remember, 2/3 of the defendants are innocent! On the other hand, she will apply the Bayes’ rule if she sees a guilty report. The probability that the defendant is guilty, given the prosecutor provided a guilty report, P(g|G-R), is

P(g|G-R) = P(G-R|g) x P(g) / [P(G-R|g) x P(g) + P(G-R|i) x P(i)]
= 1 x (1/3) /[1 x (1/3) + (3/7) (2/3)]
= (1/3)/(13/21) = 0.54

The judge will convict the defendant since the probability is > 50%. So, the overall conviction rate is 100 – 40 = 60%. The prosecutor’s incentive is 0.6. 

Conclusion

So, persuasion is the act of exploiting the sender’s information edge to influence the receiver’s decision-making. As long as the sender mixes up the flow of information to the judge, she can maximise the decisions in her favour, in this case, from 33% to 60%. 

Emir Kamenica and Matthew Gentzkow, American Economic Review 101 (October 2011): 2590–2615

Bayesian Persuasion Read More »

Response Bias

This type of bias is common in surveys, where the individual’s answer tends to be inaccurate or non-representative of the population. It can significantly impact the research; we will see some common types here. 

Voluntary response bias

The people who responded to the survey differed from the general population due to their personal experience. A typical example is the star rating, in which people with extreme experiences, either highly satisfied or highly unsatisfied, tend to respond more often than those with average experience. 

Social response bias

Also known as the social desirability bias, this bias occurs when individuals choose to respond in a way that makes them look good in front of others. In the end, good behaviour is overreported, and bad behaviour is underreported. 

Non-response bias

Suppose the people who participate in the survey are systematically different from those who don’t. A telephonic survey, say via land phone, is an example that collects only the people available at home during the calling hours. 

Response Bias Read More »