The Guessing Game
A student is attempting an exam with multiple-choice questions with four options for each question. She knows the correct answer for half of the questions and plans to guess the other half.
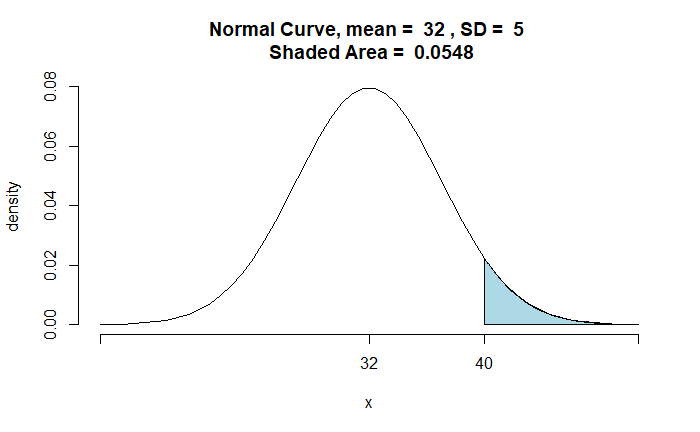
If a given response is correct, what is the probability that she guessed that answer?
Let P(G) be the probability for her to guess an answer, which we know is half or 1/2. P(G’), the probability she did not assume (because she knows the answer), is 1 – P(G) = 1/2. If she guesses an option, the chance that it is correct is P(C|G) = 1/4 (one in four). On the other hand, P(C|G’), where she did not guess, the probability for it to be correct is 1.
The required probability is P(G|C), or the chance that she guessed, given the correct answer.
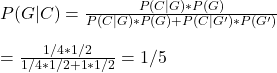
20% chance.