August 2022

A Pair of Aces

Here is a simple probability problem that can baffle some of you. I have two decks of well-shuffled cards on the table. Take out the top card of each pack. What is the probability that at least one card is an ace of spade?

The probability of finding an ace of spades from the first deck is 1 in 52 and the same in the second deck is 1/52. Since the two decks are independent, you add the probability, i.e., 2/52 = 1/26. Right? Well, the answer is not correct! So what about (1/52)x(1/52) = 0.00037? That is something else; the probability of finding both the top cards is aces of spades. But we are interested in at least one.

You obtain the correct answer as follows:
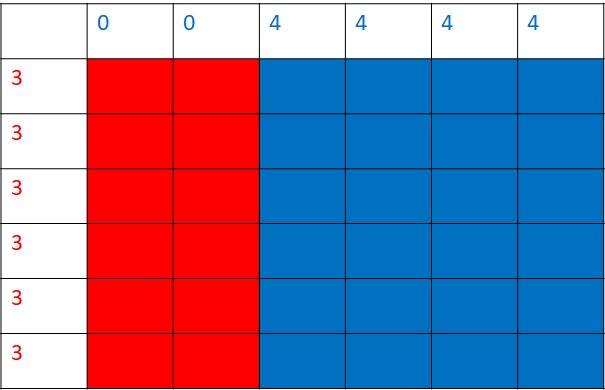
The probability of finding no ace of spades on the top of the first deck is 51/52. The same is the chance of seeing none from the second deck. Therefore, the probability of catching no ace of spades from either deck is (51/52)x(51/52). The probability of obtaining at least one equals 1 – the probability of getting none. So, it is 1 – (51/52)x(51/52) = (52 x 52 – 51 x 51)/ (52 x 52) = 103/2704 = 0.0381.

Another way of understanding this probability is to estimate all the possible ways of pairing two cards, one from each deck, containing at least one ace of spades and then dividing it by the total number of pairs. Taking an ace from the first deck, you can have 52 combinations from the second and vice versa. So there are 52 + 52 = 104 combinations. Then you have to remove the double counting two aces, reaching 103. The total number of pairs is 52 x 52 = 2704. That leaves the required quantity to be 103/2704.

The Monty Hall Problem: Jason Rosenhouse

A Pair of Aces Read More »

Waiting for a Car

If the probability of finding at least one car on the road in 30 minutes is 95%, what is the chance of finding at least one car in 10 minutes?

Let p be the probability of not finding a car in 10 minutes so that the required probability, the probability of finding at least one car in 10 minutes, is 1- p.

The probability of finding no car in 30 minutes is a joint probability of three consecutive intervals of 10 minutes each of no cars. I.e., p x p x p = p3. But this is equivalent to 1 – the probability of finding at least one car in 30 minutes. In other words 1 – p3 = 0.95. p = cube root of (1 – 0.95) = 0.368.

So, the required probability, (1 – p) becomes 1 – 0.368 = 0.63 or 63%

Waiting for a Car Read More »

Evolution of Cooperation

The foundation of cooperation is not really trust, but the durability of the relationship

Robert Axelrod, The Evolution of Cooperation

We have seen the right strategy for the basic prisoner’s dilemma problem with one play. Defect, and get the better incentive no matter what the other player does. But when it comes to an infinite game, where the same two players play several games, there can be strategies that can make better payoffs than just defect, defect, defect!

University of Michigan Professor of Political Science and Public Policy Robert Axelrod invited experts from game theory to submit programs for a computer infinite prisoner’s dilemma game. Prof Axelrod would then pair off the strategies and find the winner. The winning design was the so-called Tit for Tat, in which the player starts with cooperation and then mirrors what the other player does.

Reciprocation

Let’s see five games between A and B in which A follows the Tit for Tat method. The payoff is similar to what we have seen in the previous post.

As expected, A starts with cooperation but, seeing B defected, changes to defect in the second game. B realises that and continues cooperating, leading to 13 points for each.

Here is the game with two Tit-for-Tat gamers, both starting with cooperation.

Very peaceful game, and each ends up with 15 points. Imagine the same game, but, for some reason, B starts with a defection.

The payoffs are fine; each defector gets five each time, but the games will follow an alternative pattern.

Evolution of Cooperation Read More »

Infinite Prisoner’s Dilemma

You know what a prisoner’s dilemma is. Here, each prisoner optimises the incentive (minimises the downside) by betraying the other. And the payoffs matrix is,

B CooperatesB Defects
A Cooperates(3,3)(0,5)
A defects(5,0)(1,1)

But what happens when the choices are repeated? Then it becomes an infinite prisoner’s dilemma.

Infinite game

Unlike the once-off, the player in the infinite game must think in terms of the impact of her decision in round one on the action of the other in round two etc. The new situation, therefore, fosters the language of cooperation.

Cooperation

The question is: how many games do the players need to realise the need for cooperation?

Concept of discounting

Let’s start the game. In the found round, as rational players, players A and B will play defect, leading to a mediocre, but still better than the worst possible, outcome.

Infinite Prisoner’s Dilemma Read More »

Irrationality and Stupidity

The confusion of stupidity for irrationality is common but equally a misunderstanding. While being stupid and irrational may lead to the same outcome, poor decision-making, we should realise that the two are distinctly different. Most humans are not stupids; a lot of us are irrational in something or the other.

Stupidity is the error of judgement caused by inherent limitations of intelligence. Irrationality is due to risk illiteracy or the lack of knowledge of probability. One may be mitigated; the other is doubtful.

Irrationality and Stupidity Read More »

De Méré’s Paradox

What is more probable – getting at least one six in four throws of a die or getting at least one double six in 24 throws of a pair of dice?

It is a paradox because common sense (again!) tells you that both are equally probable. The probability of getting a six for a single die is (1/6), and that for two sixes from a pair of dice is (1/6)x(1/6). So by extrapolation, what happens in four throws for a single may become six times more (24) for double dice.

Well, the answer is wrong. Here is the calculation.

One dice

One dice
A) The probability of getting a six in one roll is (1/6).
B) The probability of getting no six in a roll is, therefore, (5/6).
C) The probability of getting no sixes in four rolls is (5/6)4 = 0.48.
D) The chance of getting at least one six in four throws is 1 – 0.48 = 0.52.

A pair

Following the steps above
A) The probability of getting a double-six in a pair of rolls is (1/6)x(1/6) = 1/36.
B) The probability of getting no double-six in a pair of rolls is 35/36.
C) The probability of getting no double-six in 24 rolls of a pair of rolls is (35/36)24 = 0.51.
D) The chance of getting at least one double-sixes in 24 rolls of a pair of dice is 1 – 0.51 = 0.49.

In summary

Getting one six in four rolls is more probable than getting one double-six in twenty-four.

De Méré’s Paradox Read More »

Potato Paradox

We have seen how percentages can miscommunicate severities of diseases with low prevalences. This time we will look at another counterintuitive fact, but here, an opposite perception, showing the contrast between absolute and relative quantities – the potato paradox.

Suppose I have 100 kg of potatoes with a 99% water content. It means 99% water and 1% solids. And if I dry them to reduce their moisture content from 99 to 98%, what is the final weight of my potatoes?

Let’s perform the calculations.
Initial weight of potatoes = 100 kg
Initial water content = 99%
Initial weight of water = 99kg
Initial weight of solids = 1 kg.

Now, drying doesn’t reduce the solids.

Final weight of solids = 1 kg.
Final water content = 98%
Final solid content = 100 – 98 = 2%

If 1 kg of solids represents 2% (0.02) of a mix, the weight of the mix is 1 (kg) / 0.02 = 50 (kg). So the final weight of potatoes is 50 kg, half of the original, and the drying just managed to reduce the moisture content from 99 to 98%!

Potato Paradox Read More »

The weatherman is Always Wrong

It is easy to prove your weatherman is wrong. Easier if you are short-term memory and are oblivious to probability.

Imagine you tune into your favourite weather program; the prediction was: a 10% chance of rain today. You know what it means: almost a dry day ahead. The same advice continued for the next ten days. What is the chance there was rain on at least one of those days? The answer is not one in ten, but two in three!

You can’t get the answer by guessing or using common sense. You must know how to evaluate the binomial probability. For instance, to calculate the chance of getting at least one rain in the next ten days, you use the formula and subtract it from one.

Decision making

All these are nice, but how does this forecast affect my decision-making? The decision (take a rain cover or an umbrella) depends on the threats and alternate choices. On a day with a 10% chance of rain predicted, I will need a reason to take an umbrella, whereas, on a day of 90%, I need a stronger one not to take precautions.

Why the weatherman is wrong

Well, she is not wrong with her predictions. But the issue lies with us. Out of those tens days, we may remember only the day it rained because it contradicted her forecast of 10%. And the story will spread.

The weatherman is Always Wrong Read More »

Efron’s Impossible Dice

Here we are, with another dice dual. I hope you recall the last banana problem. The setting is the same; there are two dice to roll, and the player who gets the higher number will win. But there is a problem the dice are not the normal ones like we know.

But they are of the four following ones.

Angela and Ben are playing this game. Angela has the advantage of choosing the first die; Ben then picks from the remaining three. Which one should Angela pick? Can Angela win this game at all?

Angela thinks we can win this, for she has the first chance to choose. She compares purple and green. Let’s see what she gets. Here is the R code. 

repeat_game <- 10000

win_perc_A <- replicate(repeat_game, {

   die_cast1 <- sample(c(2,2,2,2,6,6), size = 1, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))
   die_cast2 <- sample(c(1,1,1,5,5,5), size = 1, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))
     if (die_cast1 > die_cast2) {
     counter = 1
   } else {
     counter = 0
   }

}
)
mean(win_perc_A)

Well, the green wins two out of three. Here are all the possibilities in a tabular form.

She then compares green and red, and the outcome favours red:.

Finally, the blue and the red, and the former wins.

Since purple < green < red < blue, she thinks, blue is the winner die. And she picks it. When angela chose blue, Ben took the last one – purple. Look at the outcome.

Purple defeats blue!

Bradley Efron, professor of statistics and biomedical data science at Stanford University, is the man behind the invention of these dice. The interesting fact is that no matter which one the first person chooses, the second person always selects something better.

Efron’s Impossible Dice Read More »

Arriving at the Conditional Probabilities

We have seen the concepts of joint and conditional probabilities as mathematical expressions. Today, we discuss an approach to understanding the concepts using something familiar to us – using tables.

Tabular power

Tables are a common but powerful way of summarising data. Following is one summary from a hypothetical sample collection of salary ranges of five professionals.

It is intuitive for you to know that the values inside the table are the joint occurrences of the row attributes (professions) and column attributes (salary brackets). You get something similar to a probability once you divide these numbers by the total number of samples (= 1000). In other words, the values inside the table give us the joint probabilities.

Can you spot the marginal probabilities, say, that of doctors in that sample space? Add the numbers of the rows or columns; you get it.

Conditional probabilities

What are the chances it is a doctor if the salary bracket is 100-150k per annum? You only need to look at the column for 100-150k (because that was given) and then calculate the proportion of doctors in it. That is 0.005 out of 0.125 or 0.005/0.125 = 0.04 or 4%.

Look it this way: in the sample space, were 125 people in the given salary bracket, of which five were doctors. If the sample holds it for the population, the percentage becomes 5/125 or 4%.

The calculation can also work in the other way. What is the probability of someone in the salary bracket of 200-350k per year, given the person is a doctor? Work out the math, and you get 76%.

Arriving at the Conditional Probabilities Read More »