Life

Strictly and Weakly Dominant Strategies

After a brief break, we are back to the game theory topic. We know what a dominant strategy is. In a game, it is a player’s go-to strategy, regardless of what the other players do. The most famous example is the Prisoner’s dilemma, where Prisoner 1 has a dominant strategy – to betray—regardless of what Prisoner 2 does. There are two types of dominance. 

A strictly dominant strategy: Always provide the player with a greater (never equal to) payoff.

A weakly dominant strategy: Provide at least as good as the other strategies. At least one payoff is strictly greater.

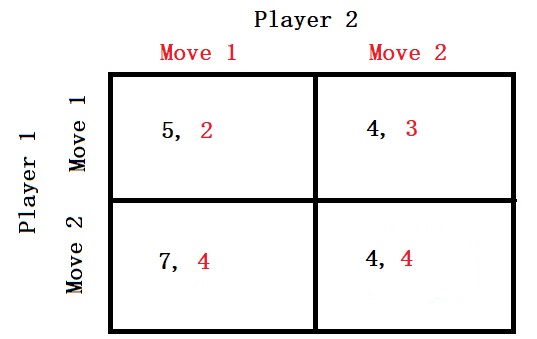
In this game, from Player 1’s perspective, if Player 2 makes move 1, Player 1 gains a better payoff by making move 2 (7 > 5). On the other hand, if Player 2 makes move 2, Player 1 has no strictly better payoff (between move 1 and move 2). So, player 1 is good to make the move 2; however, it is a weakly dominant strategy.  

Strictly and Weakly Dominant Strategies Read More »

The 17 Coins Game

Another game Played between two players. In this case, 17 coins are placed in a circle. A player can take one or two coins in her turn. In the case of the two, they must be next to each other, i.e., there must be no gap between them. Whoever takes the last coin wins. Like before, the game offers an advantage to one person. Who is it, and what is her winning strategy?

Well, the advantage is with the second person. Here is the strategy: 

Case 1: the first person takes one coin

The second person must take two coins from the opposite side, breaking down the arc into two – with seven coins each. 

From now on, the game is simple: copy what the first person does on one of the arcs to the opposite arc. Since your turn is second, you will be the one who ends the game. 

Case 2: the first person takes two coins

The second person must also create two arcs with seven coins each by removing one from the diametrically opposite end. The rest is the same as before.  

Can You Take the Final Coin? A Game Theory Puzzle: William Spaniel

The 17 Coins Game Read More »

The 21 Flags Game

Here is a game played between two parties, each taking turns. There are 21 flags. The first person, in her turn, must pick up one, two or three flags—the game shifts to the second one to do the same. The game continues. The person who picks up the last flag is the winner. In theory, the game offers an advantage to one person. Who is it, and what is her winning strategy?

As with many games, this can also be solved by thinking backwards. Imagine only one flag remaining; the person whose turn comes up wins. The same is true for two and three flags, as she can take one, two, or three in her turn. Let’s denote that person – the first in line – 1.

1 wins 1, 2, 3

There are now four flags. Person 1 can remove one, two, or three, but the last chance is for person 2. 

1 lose: 4

If there are five flags, 1 can choose one flag, and 2 is left with a four-flag situation, i.e. 2 loses. The same is true for six and seven.

1 wins 1, 2, 3, 5, 6, 7

In the case of Eight Flags, if 1 takes one, two or three, 2 gets one of the winning numbers (8-1 = 7, 8-2 = 6 or 8-3 = 5).

1 lose: 4, 8

Continuing this pattern, person 1 can win when the flags in her turn are 1, 2, 3, 5, 6, 7, 9, 10, 11, 13, 14, 15, 17, 18, 19, and 21 and will lose when the flags are 4, 8, 12, 16, 20.

Since 21 is on person 1’s list, she can win this game by always picking the flags, leaving a multiple of four to the opponent. So, at the beginning of the game, the starter picks up one flag, leaving the opponent to choose next. Person 2 can leave 19, 18, or 17 for person 1. Person 1 will then pick such that person 2 gets 16. The game goes on, and 1 eventually wins.

Can You Solve The 21 Flags Game From Survivor?: MindYourDecisions

The 21 Flags Game Read More »

Cavaliers AND LeBron AND Playoff

We have seen one extreme of the AND rule of probability, where people forget to realise how the conjunction makes events rarer. A well-known case is Linda’s problem. Here is the pictorial representation of the AND rule, which combines three events. 

The shaded region shows the joint probability of A, B, and C. As the number of events increases, the ‘common area’ shrinks. There is another extreme case of conjunction fallacy, typically used by journalists. Read the following title that appeared in CBS Sports. 

Cavaliers win first playoff series without LeBron James since 1993 by taking Game 7 over Magic

The writer has combined Cleaveland’s playoff entry, the first-round victory, and Lebron’s absence, making it a ‘rare’ sensational event.  

1. Is this the first playoff entry? No, this young Cavaliers team has been playing well. They were also in the playoff last season (2022–23) but lost against the Nicks.
2. So this must be the first series win (ever)? No, they have recently made four consecutive NBA final appearances (2014-15, 2015-16, 2016-17, 2017-18). Note that these are not just one series victory; we are talking about championship finals—four times!
3. But this happened after a long time? No, the team won the first rounds in 2007-08, 2008-09 and 2009-10.
4. Then, how can I make it a rare event? Find things in common and start subtracting them. Win, Lebron, Decade, the list goes on.

Cavaliers AND LeBron AND Playoff Read More »

Bread Sales

A bread salesman makes an average of 20 cakes; what is the chance he sells an even number of cakes? 

Let’s assume the sales follow a Poisson distribution. 

Reference

Fifty Challenging Problems In Probability: Frederick Mosteller

Bread Sales Read More »

Mother vs Girlfriend

Adam finishes work at random times between 3 PM and 5 PM. His mother lives uptown, and his girlfriend lives downtown. After work, he goes to the metro station, catches the first train in either direction and has dinner with the person who lives on the side he reaches. His mother complains that his son came only two times in the last twenty working days, whereas Adam thought he was fair, with either party getting 50-50 chances. What’s really happening? 

Suppose the metro on each side runs every 10 minutes, making it six times an hour: 3:00, 3:10, 3:20, etc. Let D represent the metro to downtown and U to uptown at x minutes after D. 

Since the mother saw him only twice in twenty days, the probability of Adam catching the uptown metro is 2/20 = 1/10, which must be equal to x/10. This implies x = 1. So the metro that goes uptown reaches its stop at 3:01, 3:11, 3:21, etc.

Reference

Fifty Challenging Problems In Probability: Frederick Mosteller

Mother vs Girlfriend Read More »

Bayesian Persuasion

Persuasion is the act of a person (a.k.a. the sender) to convince another (the receiver) to decide in favour of the sender. Suppose the receiver is a judge and the sender is the prosecutor. The prosecutor aims to make the judge convict 100% of the defendants. But the judge knows that only a third of the defendants are guilty. Can the prosecutor persuade the judge to get more than 33% of the decisions in her favour? If the judge is rational, what should be the prosecutor’s strategy?  

Suppose the prosecutor has the research report and the knowledge about the truth. She can follow the following three strategies.

Strategy 1: Always guilty

The prosecutor reports that the defendant is guilty 100% of the time, irrespective of what happened. In this process, the prosecutor loses credibility, and the judge resorts to the prior probability of a person being guilty, which is 33%. The result? Always acquit the defendant. The prosecutor’s incentive is 0. 

Strategy 2: Full information

The prosecutor keeps it simple – report what the research finds. It makes her credibility 100%, and the judge will follow the report, convicting 33% and acquiring 66%. The prosecutor’s incentive is 0.33. 

Strategy 3: Noisy information

Here, when the research suggests the defendant is innocent, report that the defendant is guilty slightly less than 50% of the time and innocent the rest of the time. Let this fraction be 3/7 for guilty and 4/7 for innocent. 

From the judge’s perspective, if she sees an ‘innocent’ report from the prosecutor, she will acquit the defendant. The proportion of time this will happen is (2/3) x (4/7) or 40%. Remember, 2/3 of the defendants are innocent! On the other hand, she will apply the Bayes’ rule if she sees a guilty report. The probability that the defendant is guilty, given the prosecutor provided a guilty report, P(g|G-R), is

P(g|G-R) = P(G-R|g) x P(g) / [P(G-R|g) x P(g) + P(G-R|i) x P(i)]
= 1 x (1/3) /[1 x (1/3) + (3/7) (2/3)]
= (1/3)/(13/21) = 0.54

The judge will convict the defendant since the probability is > 50%. So, the overall conviction rate is 100 – 40 = 60%. The prosecutor’s incentive is 0.6. 

Conclusion

So, persuasion is the act of exploiting the sender’s information edge to influence the receiver’s decision-making. As long as the sender mixes up the flow of information to the judge, she can maximise the decisions in her favour, in this case, from 33% to 60%. 

Emir Kamenica and Matthew Gentzkow, American Economic Review 101 (October 2011): 2590–2615

Bayesian Persuasion Read More »

The Rating Problem

Here is the rating summary of a product,
Good – 40%
Average – 10%
Poor – 50%
Looking at the product, how do you know which view represents the actual quality of the product?

Can we conclude that the probability of the product being good equals 0.4, average 0.1, and poor 0.5? Although that is what we want from the rating system, we must realise that these may not represent the absolute or marginal probability of quality but the conditional probability, e.g., the probability of good a given person has rated. In other words

P(Good|Rated) = 0.4
P(Average|Rated) = 0.1
P(Poor|Rated) = 0.5

From this information, we can estimate the actual probabilities, P(Good), P(Average) and P(Poor) using Bayes’ theorem. 

P(Good|Rated) = P(Rated|Good) x P(Good) / P(Rated)
P(Average|Rated) = P(Rated|Average) x P(Average) / P(Rated)
P(Poor|Rated) = P(Rated|Poor) x P(Poor) / P(Rated)

The Rating Problem Read More »

The Bayesian Runner

Becky loves running 100-meter races. The run timing for girls her age follows a normal distribution with a mean of 15 seconds and a standard deviation of 1s. The cut-off time to get into the school team is 13.5 seconds. If Becky is on the school running team in 100 meters, what is the probability that she runs below 13 seconds?

Without any other information, we can use the given probability distribution to determine the chance of Becky running under 13 seconds.

pnormGC(13,region="below", mean=15,sd=1.,  graph=TRUE)

Since we know she is in the school team, we can update the probability as per Bayes’ theorem. Let’s use the general formula of Bayes’ theorem here:

\\ P(13|T) = \frac{P(T|13)*P(13)}{P(T)}

The first term in the numerator, P(T|13) = 1 (the probability of someone in the team with a cut-off of 13.5 s, given her timing is less than 13s). We already know the second term, P(13), 0.0228.

The denominator, P(T), is the probability of getting on the team, which is nothing but the chance of running under 13.5 seconds. That is, 

pnormGC(13.5,region="below", mean=15,sd=1.,graph=TRUE)

Substituting P(T) = 0.0668 in the Bayes equation,

P(13|T) = 0.0228/0.0668 = 0.34 or 34%

The Bayesian Runner Read More »

Begging the Question

A person new to religion may have questions about the credibility of its belief system. For example, how do I know the way God operates? A person with a Christian belief system will tell you it’s written in the Bible. But how do I know the Bible is telling the truth? I did a search, and one of the results on the validity of the scriptures was the King James Bible online. The first one was:

“2 Timothy 3:16 – All scripture is given by inspiration of God, and is profitable for doctrine, for reproof, for correction, for instruction in righteousness:” 

If you are happy with the answer, like millions of people, you have committed the fallacy of begging the question. Begging the question is a complicated way of describing a circular reasoning, where an argument’s premise assumes the truth of the conclusion.

An argument has three parts:
1. Claim or conclusion – presented upfront
2. Support or evidence – presented to back the claims
3. Warrant or major premise – hidden in the argument but bridges the support to the claim.

Consider the following argument. 

In the fallacy of circular argument, the claim (Bible is telling the truth) takes the evidence (verses from the book of Timothy) from the same book to prove the claim.

Data & Statistics on Autism Spectrum Disorder: CDC

Begging the Question Read More »