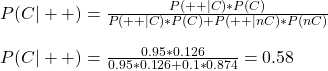Data & Statistics

Cars No Safer

April 11, 2022

Calculating the risk numbers for passenger cars is a lot harder than the air. First, the data gathering is more challenging, thanks to the sheer number of vehicles on the road. The next thing is to estimate the number of car crashes a year. But, let’s make an attempt.

As per wiki, globally, about 1.4 billion motor vehicles are in use; a billion of them are cars. We don’t know how many journeys those make. Assuming an average of 100 days, you get 200 billion trips a year.

We use some shortcuts to estimate the number of crashes involving cars. India, which accounts for 11% of global death from road accidents, reports 150,000 fatalities from 450,000 incidents in a year. By extending the logic to the global scale, for the 1.3 million deaths every year, we estimate the incidents to be four million. We try yet another way of estimation. About 50 million injuries happen every year from vehicles and let’s assume half of them involve people travelling in the car (same ratio of reported death). The rest of them involves pedestrians and cyclists. Assuming an average of 3 people inside, we can estimate 25/3 = 8.3 million cars involved in incidents.

In the same way, 1.3 million deaths every year translates to 650,000 involving car travellers. That suggests a maximum of 650,000 fatal incidents and a minimum of 200,000 fatal incidents. Assume a mid-value of 400,000. Let’s compile all these (reported and assumed) into a table.

Item	Data
# of car trips	200 bln (estimated)
# road incidents	4 – 8 mln (estimated)
# fatal incidents	400,000 (estimated)
# deaths	650,000 (estimated)
# passengers	600 bln (estimated)
average trip length	20 km (estimated)
passenger-km	12000 bln-km (estimated)

Calculated quantities

Metric	Data
Incidents per trip	20 – 40 (per million trips)
Fatal incidents per trip	2 (per million trips)
Fatality per trip	3.2 (per million trips)
Fatality per passenger-km	54 (per billion-km)
Fatality per passenger	0.81 (per million passengers)

Now compare these with what we had estimated previously for the air.

Comparison – air travel

Metric	Data
Incidents per trip	3.13 (per million trips)
Fatal incidents per trip	0.2 (per million trips)
Fatality per trip	14.4 (per million trips)
Fatality per passenger-km	0.06 (per billion-km)
Fatality per passenger	0.13 (per million passengers)

Looks like air travel is safer on all counts.

References

[1] http://www.rvs.uni-bielefeld.de/publications/Reports/probability.html
[2] https://economictimes.indiatimes.com/news/politics-and-nation/india-tops-the-world-with-11-of-global-death-in-road-accidents-world-bank-report/articleshow/80906857.cms
[3] https://en.wikipedia.org/wiki/Aviation_accidents_and_incidents
[4] https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries
[5] https://www.icao.int/annual-report-2019/Pages/the-world-of-air-transport-in-2019.aspx
[6] https://data.worldbank.org/indicator/IS.AIR.PSGR
[7] https://en.wikipedia.org/wiki/Aviation_safety
[8] https://accidentstats.airbus.com/statistics/fatal-accidents
[9] https://injuryfacts.nsc.org/home-and-community/safety-topics/deaths-by-transportation-mode/
[10] https://www.sciencedaily.com/releases/2020/01/200124124510.htm

Cars No Safer Read More »

Riskier Flights

April 10, 2022

That flight travel is one of the safer modes of transportation is a foregone conclusion. Yet, there seems to be some confusion about the risk of taking flights versus, say, cars. Therefore the comparison requires a reevaluation.

The first question is: what is the right metric to use? Is it the number of fatalities per passenger boarding? Or is it the number of accidents/deaths per boarding? Yet another one is the number of accidents/deaths per passenger-kilometre travelled. Let’s make some (gu)estimates on each of these.

Available data

Item	Data
# of flights	40 mln (2019)
# aviation incidents	125 (2019)
# fatal accidents	8 (2019)
# aviation deaths	575 (2019)
# passengers	4500 mln (2019)
average trip length	2000 km
passenger-km	9000 bln (2019)

Calculated quantities

Metric	Data
Incidents per trip	3.13 (per million trips)
Fatal incidents per trip	0.2 (per million trips)
Fatality per trip	14.4 (per million trips)
Fatality per passenger-km	0.06 (per billion-km)
Fatality per passenger	0.13 (per million passengers)

Risk of air travel

In my option, the right metric is either the number of incidents per trip or the number of fatal incidents per trip. And probably the difference between road vs air. In air travel, the distance covered or the number of hours in the air are not the prime variable for incidents; riskier parts of a flight are the takeoff and landing, each of which happens once every trip, however brief or lengthy the travel be.

Comparison with the road

So how does it compare with road travel? That is a bit more complex as the data are hard to come by, requiring a lot of assumptions. Also, the risk of road travel has not distributed the way it is for the air. We’ll visit those in another post.

References

Riskier Flights Read More »

Florida and Sibling Stories

April 9, 2022

We have seen the girl paradox in one of the older posts. Today we do a series of variations of the problem using Bayes’s equation. Sorry, Bayes-Price-Laplace equation! In a town far far away, every household has exactly two children.

The probability of two girls in a family

$\\ P(GG) = \frac{1}{4}$

The probability of two girls in a family, if you know, they have at least one girl.
We use the generalised equation here.

$\\ P(GG|1G) = \frac{P(1G|GG)*P(GG)}{P(1G|GG)*P(GG) + P(1G|GB)*P(GB) + P(1G|BG)*P(BG) + P(1G|BB)*P(BB)} \\\\ = \frac{1*\frac{1}{4}}{1*\frac{1}{4} + 1*\frac{1}{4} + 1*\frac{1}{4} + 0*\frac{1}{4}} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3}$

I guess you don’t need a lot of explanations. B represents a boy, and G represents a girl. The prior probability of each combination, BB, BG, GB or GG, is (1/4); equally likely.

The probability of two girls in a family, if you know, a family has a girl named Florida. Florida is a girl’s name, and let p is the probability of a girl named Florida.

$\\ P(GG|F) = \frac{P(F|GG)*P(GG)}{P(F|GG)*P(GG) + P(F|GB)*P(GB) + P(F|BG)*P(BG) + P(F|BB)*P(BB)} \\\\ = \frac{[p(1-p)+(1-p)p+p^2]*\frac{1}{4}}{[p(1-p)+(1-p)p+p^2]*\frac{1}{4} + p*\frac{1}{4} + p*\frac{1}{4} + 0*\frac{1}{4}} = \frac{(2p-p^2)*\frac{1}{4}}{(2p-p^2)*\frac{1}{4} + p*\frac{1}{4}} = \frac{2-p}{4-p}$

You may be wondering where that long-expression for P(F|GG) comes from. It’s the total probability of having a girl named Florida, regardless of whether they have already a daughter named Florida. So p(1-p) (the first girl is Florida and the other girl is not), (1-p)p (the second girl is Florida and the other girl is not), and p² (both girls are Florida).

This is interesting. If the probability of a girl’s name Florida is 1, or every girl is named Florida, then P(GG|F) = (1/3) = P(GG|1G). If the name is rare or close to zero, P(GG|F) becomes (1/2).

Florida and Sibling Stories Read More »

A Laplace Equation Named Bayes

April 8, 2022

You may be wondering at the title of this post. Well, it is true – it was Laplace who made the Bayes equation. But not the Bayes theorem!

Bayes theorem may have been postulated a few years before Pierre Simon Laplace was born, in 1749. Bayes’ view about probabilities was more conceptual. It was a simple idea of modifying our subjective knowledge with objective information. In more technical language: initial (subjective) belief (guess or prior) + objective data = updated belief. Interestingly, those two words – subjective and belief – made classical statisticians, aka frequentists, mad!

Laplace, unaware of what Bayes had done more than two decades before, had his own ideas about the probability of causes. Eventually, he came up with a theory: the probability of a cause (given an event) is proportional to the probability of the event (given the cause). Note how close he has come to the Bayes formula that we know today.

It took Laplace another eight years or so to learn about Bayes’ idea of a prior, which gave Laplace’s equation the form as we know it. Well, by the name Bayes equation!

A Laplace Equation Named Bayes Read More »

When It’s No Longer Rare

April 7, 2022

Let us end this sequence of Sophie and her cancer screening saga. We applied Bayes’ theorem and showed that the probability of having the disease is low, even with a positive test result. But the purpose was not to downplay the importance of diagnostics tests. In fact, it was not about diagnostics at all!

Screening a random person

Earlier, we have used a prior of 1.5% based on what is generally found in the population (corrected for age). And that was the main reason why the conclusion (the posterior) was so low. It was also considered a random event. Sophie had no reason to suspect a condition; she just went for screening.

Is different from Diagnostics

You can not consider a person in front of a specialist as random. She was there for a reason – maybe discomfort, symptoms, or recommendation from the GP after a positive result from a screening. In other words, the previous prior of 1.5% is not applicable in this case; it becomes higher. Based on the specialist’s database or gutfeel, imagine that the assigned value was 10%. If you substitute 0.1 as the prior in the Bayes’ formula, we get about 50% as the updated probability (for the set of screening devices).

Typically, the diagnostic test would have a better specificity. If the specificity goes up from 90 to 95%, the new posterior becomes close to 70%. It remains high, even if the sensitivity of the equipment dropped from, say, 95% to 90%.

When It’s No Longer Rare Read More »

Why Posterior is the New Prior?

April 6, 2022

So far, we have been accepting the notion that the posterior probability from the Bayes’ equation becomes the prior when you repeat a test or collect more data. Today, we verify that argument. What is the chance of having the disease if two independent tests turned positive? Let’s write down the equation.

$\\ P(D|++) = \frac{P(++|D)*P(D)}{P(++|D)*P(D) + P(++|nD)*(1-P(D))}$

Since the two tests are independent, and the marginal probability of the two positive tests is similar, we can write P(++|D) as the joint probability, P(+|D)*P(+|D). The same is true for the false positives, P(++|nD). Substituting all of them, we get

$\\ P(D|++) = \frac{P(+|D)*P(+|D)*P(D)}{P(+|D)*P(+|D)*P(D) + P(+|nD)*P(+|nD)*(1-P(D))}$

P(+|D) is your sensitivity, P(+|nD) is 1 – specificity and P(D) is the assumed prior.

Now, we will go to the original proposition of the posterior becoming the next prior. The probability of having the disease given the second test is also positive is given by

$\\ P(D|2nd +) = \frac{P(2nd +|D)*P(D|1st+)}{P(2nd +|D)*P(D|1st+) + P(2nd+|nD)*(1-P(D|1st+))} \\ \\ \text{where, } \\ \\ P(D|1st+) = \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} \\ \\ \text{since these tests are independent}, P(2nd +|D) = P(+|D) \text{. Substituting, } \\ \\ P(D|2nd +) = \frac{P(+|D)*P(D|1st+)}{P(+|D)*P(D|1st+) + P(+|nD)*(1-P(D|1st+))} \\ \\ = \frac{P(+|D)* [ \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} ] }{P(+|D)* [ \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} ] ) + P(+|nD)*(1- [ \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} ] )} \\ \\ \text{expanding and cancelling similar terms,} \\ \\ P(D|2nd +) = \frac{P(+|D)*P(+|D)*P(D)} {P(+|D)*P(+|D)*P(D) + P(+|nD)*(1-P(D))} = P(D|++)$

Yes, posterior is the new prior! If you generalise the equation for n number of independent tests,

$\\ P(D|+n) = \frac{P(+|D)^n*P(D)}{P(+|D)^n*P(D) + P(+|nD)^n*(1-P(D))}$

Why Posterior is the New Prior? Read More »

Equation of Life Revisited

April 5, 2022

I guess you remember the story of Sophie that we encountered at the start of our journey with the equation of life. She has tested positive during a cancer screening but found that the probability of the illness was about 12% after applying Bayes’ principles. There was nothing faulty about the test method, which was pretty accurate, at 95% sensitivity and 90% specificity. Now, how many independent tests does she need to undertake to confirm her illness at 90% probability?

Assume that her second test was positive: The probability for Sophie to have cancer, given that the second test is also positive,

$\\ P(C|++) = \frac{P(++|C)*P(C)}{P(++|C)*P(C) + P(++|nC)*P(nC)} \\ \\ P(C|++) = \frac{0.95*0.126}{0.95*0.126 + 0.1*0.874} = 0.58$

The updated probability has become 56% (note we have used 12.6%, which is the posterior of the first examination, as the prior and not the original 1.5%). Applying the equation one more time for a positive (third by now) test, you get

$\\ P(C|++) = \frac{0.95*0.58}{0.95*0.58 + 0.1*0.42} = 0.93$

So the answer is three tests to get a high level of confidence.

You may recall that the prior probability used in the beginning was 1.5%, based on what she found in the American Cancer Society publications. What would have happened if she did not have that information? She still needs a prior. Let’s use 0.1% instead. Let’s work on the math, and you will find that about 89% probability can reach in the fourth test, provided all are positive. Therefore, an accurate prior is not that crucial as long as you follow up with more data collection, which is the power of the Bayesian approach.

Equation of Life Revisited Read More »

Another Game Behind Closed Doors

April 4, 2022

We have seen the Monty Hall problem in an earlier post. This time, instead of 3, we have four doors. There is $1000 behind one door, -$1000 behind another (you lose $1000), and two other doors have nothing ($0). Like in the previous game, you choose one door, and then the game host opens a door that contains nothing. You have an option to change to one of the other closed doors now. What will you do?

No Change

In the beginning, before hosts reveals the $0 door, the probabilities are P($1000) = 1/4, P($0) = 1/2 and P(-$1000) = 1/4. The expected return is (1/4) x $1000 + (1/2) x $0 + (1/4) x -$1000 = $0. After the clue, if you still don’t want to change, this remains the case.

Change

Here, we use solution 2, the argument method, of the Monty Hall problem. Before you get the clue, the chance that you chose the $1000 door is 1/4, and that the prize was outside your choice is 1 – 1/4 = 3/4. After the clue, that probability of 3/4 sits behind two doors. In other words, if you shift, the chance of getting $1000 is 3/8. Using similar arguments, we shall see that the chance of losing became 3/8, and for $0 is 1/4. The expected return is (3/84) x $1000 + (1/2) x $0 + (3/8) x -$1000 = $0.

Will you change?

Well, it depends on your risk appetite. The chance of winning and the chance of losing have increased. But the expected returns remained the same, at zero. Or the risk has increased if you shift. If you are risk-averse, stay where you are!

Another Game Behind Closed Doors Read More »

Bayesian vs Frequentist

April 2, 2022

There are two main perspectives in statistical inference. They are Baysianism and frequentism. So what are they? Let’s understand them using a coin-tossing example. It goes like this. What is the probability of getting a head if I toss a coin?

Bayesian first assumes, then update

Well, the answer depends on whom you ask! If you ask a Baysian, she will start the following way: a coin has two sides – a head and a tail. Since I don’t know whether the coin is fair or biased, I assume in favour of the former. In that case, the probability is (1/2), and then, depending on what happens, I may update my belief!

Frequentist first counts, then believe

You ask the same question to the frequentist, and she will hesitate to assume but will ask you to do the tossing a hundred times, count them and then estimate!

How can one event has two different chances?

The toss just happened, but the outcome is hidden from your sight. The question is repeated: what is the probability that it is a head? The Bayesian would still say it is (1/2). The frequentist’s perspective is different. The coin is already landed, and there is no more probability: it has to be either a head or a tail. If it is a head, the answer is 100%, but if it is a tail, the answer is 0%!

Who is right?

If you recall my old posts, I have used Bayesian mostly in calculations but frequentist for explaining things. One classic example is the weather forecast. The easiest way we can understand a 40% probable rain tomorrow is if I tell you that when such weather conditions happened in the past 100 occasions, it rained in 40 of them. And you are happy with the explanation. But in my weather model, I may have used 0.4 as a parameter and depending on what happened tomorrow (actually, it rained), I may have updated my model like a true Bayesian.

Bayesian vs Frequentist Read More »

What happened to the Past Climate Predictions?

March 27, 2022

We have seen the role of climate models to understand the magnitude of global warming. Almost all of the narratives of catastrophe from the climate commentators go back to the output of climate models. And projections from these models play a crucial role in shaping our collective consciousness and aligning global policymaking to fight against this human-made problem.

Models also contribute to why the subject of global warming gets criticism from the sceptics. To most non-physicists, mathematical models represent fantasy, unconnected to reality. Also, projections are forward-looking, and it is easy to cast doubts in public minds for its alleged function as a crystal ball. Calling such people anti-science is easy but not entirely justified; after all, science too calls for the same; get the evidence and validate your predictions. So how do we validate a model prediction for the future?

Look for the past predictions!

Hausfather and others published a paper in the geophysical research letters in 2019 that exactly went for this. The work looked at various models published between the 1970s to the late 2000s. And what did they find? The team have gathered about 15 model predictions from the past and compared them with the observed data. They found that the predictions were well within the margin of errors of the observations. The models of the 70s, 80s and 90s were pretty accurate to predict the future, which is past by now!

What is a climate model?

A model gives a connection between an input and an output. It’s achieved using the physics of the process and represented through the language of mathematics. In the context of climate change, concentrations of CO₂ in the atmosphere is the input, and the temperature rise (or fall) is the output. A typical model estimates the reason for the temperature change, i.e., the radiative forcing or the change in energy flux (the incoming – outgoing energy) on the planet. In other words, if the outgoing is less than the incoming, the temperature rises; otherwise, it falls, simple!

Why is this no news?

There are many reasons why a good match between a model and observations never makes it to the news. But, before getting there: why do you expect the predictions made by the collaborative works of 100s of top scientists to go wrong in the first place? We will explore the answer in another post. Now, let’s come back to why they didn’t become headlines. First, predictions happen today (which attracts news), but the data arrive 5-10 years later. By then, you may have forgotten about the original work! Secondly, matching an expectation does not make it sensational for the news. Imagine this news: “NASA scientists verified the physics of radiative forcing, again”! Third, a good match like this is more of a nuisance to the people who want to believe that climate change isn’t real (or who worry about the need to change the current lifestyle).

One such example is the projections made by NASA’s Hansen et al. in 1988. That story, in another post.

References

Hausfather, Z.; Drake, H. F.; Abbott, T.; Schmidt, G. A., 2020, “Evaluating the performance of past climate model projections“, Geophysical Research Letters, 47.
Climate Reports: IPCC
Introduction to Climate Models, CMIP

What happened to the Past Climate Predictions? Read More »