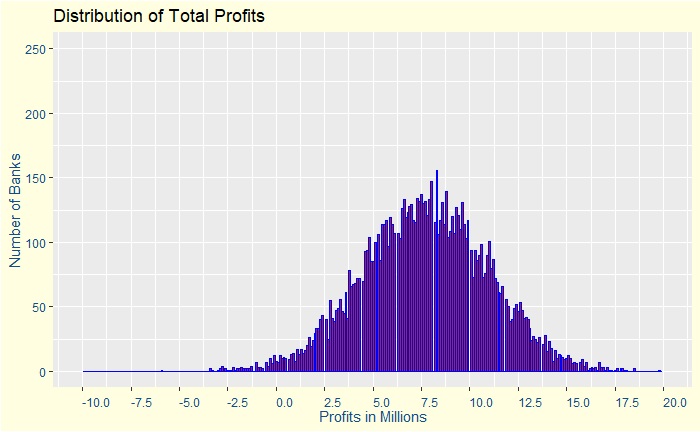
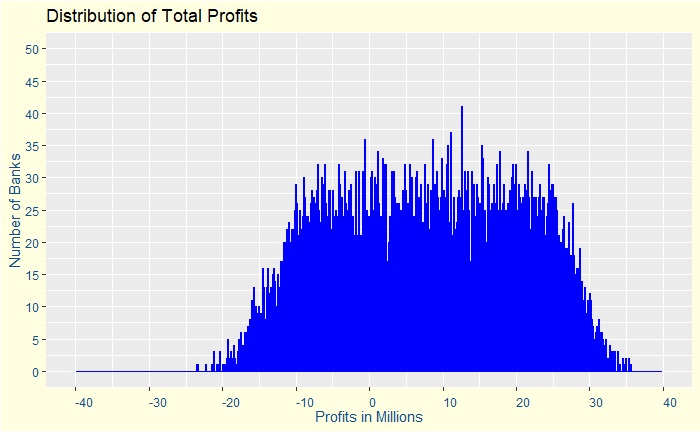
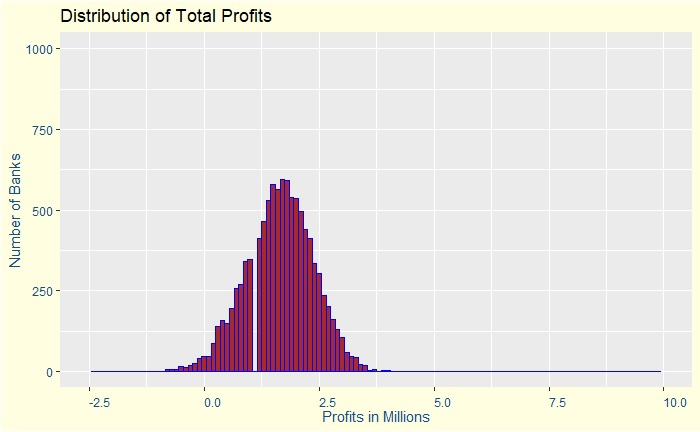
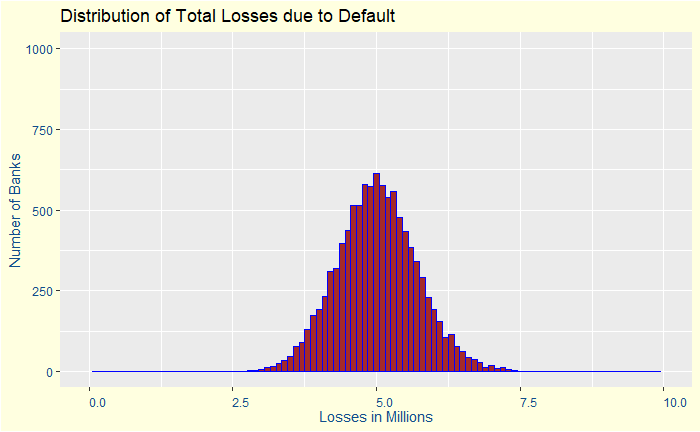
Prosecutors fallacy
We have seen that Bayes’ theorem is a fundamental tool to validate our beliefs about an event after seeing a piece of evidence. Importantly, it utilises existing statistics or prior knowledge to get to a conclusion. In other words, our hypothesis gets better representativeness by using Bayes’ theorem.
Take some examples. What are the chances that I have a specific disease, given that the test is positive? How good are my perceptions of a person’s job or abilities just by observing a set of personality traits? What are the chances that the accused is guilty, given that a piece of evidence is against her?
Validating hypotheses based on the available evidence is fundamental to investigations but is way harder than they appear, partly because of the illusion of the mind that confuses the required conditional probability with the opposite. In other words, what we wanted to find is a validation of the hypothesis given the evidence, but what we see around us is the chance of evidence if the hypothesis is true, because often, the latter is part of common knowledge.
To remind you of the mathematical form of Bayes’ theorem
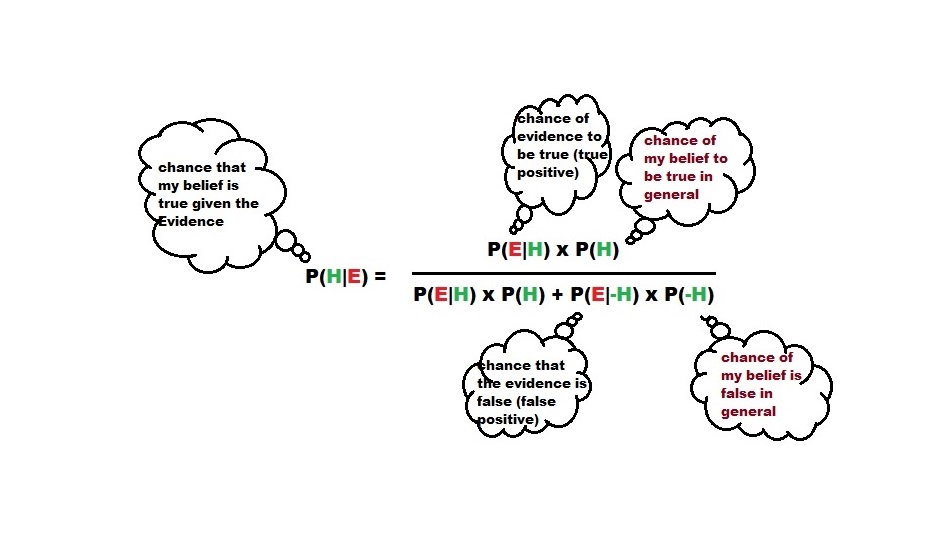
Confusion between P(H|E) and P(E|H)
What about this? It is common knowledge that a running nose happens if you have a cold. Once that pattern is wired to our mind, the next time when you get a running nose, you assume that you got a cold. If the common cold is rare in your location, as per Bayes’ theorem, the assumption that you made require some serious validation.
Life is OK as long as our fallacies stop at such innocuous examples. But what if that happens from a judge, hearing the murder case? It is the classic prosecutor’s fallacy in which the size of the uncertainty of a test against the suspect is mistaken as the probability of that person’s innocence.
chances of crime, given the evidence = chance of evidence, given crime x (chance of crime/chance of evidence). Think about it, we will go through the details in another post.
Prosecutors fallacy Read More »