The Zero-Sum Fallacy

In life, your win is not my loss. This is contrary to what used to happen when we were hunter-gatherers, fighting for a limited quantity of meat or in the sporting world, where there is only one crown at the end of a competition. And changing this hard-wired ‘wisdom of zero-sum’ requires conscious training.

The Double ‘Thank You’ Moment

In his essay, The Double ‘Thank You’ Moment, John Stossel uses the example of buying a coffee. After paying a dollar, the clerk says, “Thank you,” and you also respond with a “thank you.” Why?
“Because you want the coffee more than the buck, and the store wants the buck more than the coffee. Both of you win.”
Except under coercion, transactions lead to positive-sum games; otherwise, the loser wouldn’t have traded.

A great example of our world of millions of double thank-you moments is apparent from how the global GDP has changed over the years.

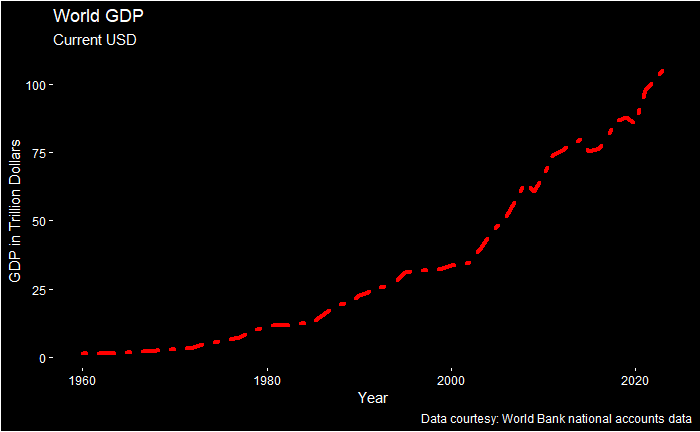
Notice that the shape of the curve is not flat but is exploding lately due to the exponential growth in transactions between people, countries and entities.

Inequality rises; poverty declines

One great tragedy that extends from the zero-sum fallacy is the confusion of wealth inequality with poverty. In a zero-sum world, one imagines that the rich getting richer must be at the expense of the poor! In reality, what matters is whether people are coming out of poverty or not.

Reference

GDP: World Bank Group
The Double ‘Thank You’ Moment: ABC news

The Zero-Sum Fallacy Read More »

Maximum Likelihood Estimation

This is my 1000th post. While the likelihood of reaching post # 1000 in as many days is one topic for a future post, today we specifically develop some intuition around MLE or the maximum likelihood estimate.

A coin lands H, H, T, T, H. How likely is this to happen? A simplistic way is to think that this coin always lands in this pattern (H, H, T, T, H). We know that is not credible. Let’s assign the coin a probability p (“the parameter”) to land heads. So, the question we want to answer is: at what probability (of occurrence for heads), p, does the likelihood maximise?

Step 1: What is the probability of observing the sequence HHTTH? Let’s assume all flips are independent. The probability is
p x p x (1-p) x (1-p) x p = p3 x (1-p)2

Step 2: What is the value of p at which the likelihood of observing HHTTH is maximised? We will take help from calculus, take a derivative, equate to zero, and solve for p.

3p2 x (1-p)2 – 2 p3 x (1-p) = 0
3(1-p) – 2p = 0
p = 3/5 = 0.6

Ok, the MLE for this sequence is 0.6. But what is the probability of the sequence happening? For that, substitute the value of p in the equation,
0.6 x 0.6 x (1-0.6) x (1-0.6) x 0.6 = 0.03456

Conclusion: if the coin lands on heads 60% of the time, the probability of seeing the sequence HHTTH is 3.456%. 3.456% may appear small, but it is better than any other p.

Continuous distribution

If a person’s height is 66 inches, which population is she from? It is unusually rare that a region has only people 66 inches tall. We assume that people’s heights follow a normal distribution with a standard deviation (say, 4). So, the question becomes: What is the most likely distribution that person is from?

Here are a few distributions with the standard deviation 4. By placing a market at x = 66, you can observe that the distribution with mean = 66 is the most likely (the highest point) to represent the observed data.

Instead, we collected two data, 66 and 58 inches. The blue curve strongly supports 66, but not much 58. MLE will balance the probabilities so that it can include both the data.

The average of 66 and 58 (= 62) will maximise the likelihood.

Reference

Maximum Likelihood Estimation: Brian Greco – Learn Statistics! 

Maximum Likelihood Estimation Read More »

Bayesian Data Analysis – A/B Testing

We have seen how Bayesian analysis is done to get the most probable parameter that would have resulted in the observed data for a single set.

  1. Data
  2. A generative model: a mathematical formulation that can give simulated data from the input of parameters.
  3. Priors: information for the model before seeing the data

This time, we analyse two sets of data and compare them. The method is similar to what we have done for the single set.

Problem statement

There were two campaigns: one received positive reviews in 6 out of 10 and the other in 9 out of 15. We must compare them and report the better method, including the uncertainty range.

Unlike before, we will run two models side by side this time. Draw a random parameter 1 value from the prior1.

prior1 <- runif(1, 0, 1)

Run the model using prior1 to estimate simulated value 1.

sim1 <- rbinom(1, size = 10, prob = prior1)

In the same way, run the second model using another uniform prior. 

prior2 <- runif(1, 0, 1)
sim2 <- rbinom(1, size = 15, prob = prior2)

Accept the parameter values (prior1 and prior2) only if the posteriors (sim1 and sim2) match the data, 6 and 9, respectively.

Now, you can find the difference between the two posteriors, resulting in a new distribution.

Reference

Introduction to Bayesian data analysis – part 2: rasmusab

Bayesian Data Analysis – A/B Testing Read More »

What to Expect When No Preference

Imagine you asked three people about their preference between apples and oranges. What would be your conclusion if the first two preferred apples and the third liked orange? Does it mean more people like Apple, or did it happen by random chance?

One way to deal with it is to test and get the probability of the hypothesis that people have no preference. So, let’s analyse what happened.

No preferred assumption means the probability of a person saying apple or orange is 0.5. The probability of the first two persons randomly choosing an apple and the third person randomly choosing an orange is,

0.5 x 0.5 x 0.5 = 0.125

But this is not what we are after. The situation can as well be the following,

or

The probability of situation 1 OR situation 2 OR situation 3 = sum of the three probabilities. It is 0.125 + 0.125 + 0.125 = 0.375.

Binomial distribution

It is the same thing we have seen in binomial probability distribution. The probability of s successes in n rounds is
nCs x ps x q(n-s)

What to Expect When No Preference Read More »

Bootstrapping

Suppose a drug was tested on eight people. Five people became better, and three did not. How do we know if the drug works? Naturally, eight is far from the population of a region, which could be in the thousands.

The bootstrapping technique fundamentally pretends that the sample histogram is the population histogram. It then performs repeated sampling (with replacement) from the collected dataset. It creates histograms of outcome statistics of what might have been obtained if the experiment had been done several times.

Here are the eight data collected. The positive values correspond to people who improved with the drug, and the negative values are the opposite.

data <- c(-3.5, -3.0, -1.8, 1.4, 1.6, 1.7, 2.9, 3.5)

Let’s randomly sample from this a hundred times, estimate the mean each time and plot the histogram of it.

resamples <- lapply(1:100, function(i) sample(data, replace = T))
boot.mean <- sapply(resamples, mean)
hist(boot.mean, breaks = 20)

Note that when randomly sampling from the dataset, some data can come multiple times; therefore, we see the histogram (distribution) of the mean.

Bootstrapping Read More »

Bayesian Data Analysis – Developing the Scheme

Let’s demonstrate the analysis using an example. An advertising campaign for a product surveyed 16 people, and 6 of them responded positively. What are the expected product sales when it is launched on a large scale?

The simplest way is to divide 6 by 16 = 38% and conclude that this is the potential hit rate. However, this has large uncertainty (due to the small sample size), and we must account for that. Remember the steps of Bayesian inference.

  1. Data
  2. A generative model: a mathematical formulation that can give simulated data from the input of parameters.
  3. Priors: information for the model before seeing the data

We have data, and we need a generative model. The aim is to determine what parameter would have generated this data, i.e., the likely rate of positive ‘vibe’ in public that would have resulted in 6 out of 16. Assuming individual preferences are independent, we can utilise the binomial probability distribution as the generative model. Now, we need the parameter value. Since we don’t know that, we use all possible values or a uniform distribution.

Now, we start fitting the model. Draw a random parameter value from the prior.

prior <- runif(1, 0, 1)
0.4751427

Run the model using 0.4751427

rbinom(1, size = 16, prob = 0.4751427)
8

Well, this doesn’t fit because the output is not 6, but 8. Repeat this sampling and model-runs several times, collect the parameter values that result in 6 and make a histogram.

The first takeaway is that parameter values below 0.1 and above 0.7 have rarely resulted in the observed data. The median posterior turns out to be 0.386.

Finding the posterior distribution is the goal of Bayesian analysis. The value 0.386 (38.6%) is the most probable parameter value that would have resulted in the observed data—the famous “maximum likelihood estimate.”

Reference

Introduction to Bayesian data analysis – part 1: What is Bayes?: rasmusab

Bayesian Data Analysis – Developing the Scheme Read More »

Bayesian Data Analysis

Earlier, we saw how John K. Kruschke explained Bayesian inference in his book, “Doing Bayesian Data Analysis”. Today, I will present another elegant description from the YouTube channel “rasmusab”. He explains Basian Data Analysis as:

“A method to figure out unknowns, known as parameters, using”

  1. Data
  2. A generative model: a mathematical formulation that can give simulated data from the input of parameters.
  3. Priors: information for the model before seeing the data

So, the objective is to estimate a reasonable set of parameter values that could have generated the data, as observed. And it is done in this fashion:
Plug in a parameter value
Run it through the generative model
Get out the simulated data
Accept only those parameter values that gave the simulated data = observed data.

Reference

Doing Bayesian Data Analysis by John K. Kruschke
Introduction to Bayesian data analysis – part 1: What is Bayes?: rasmusab

Bayesian Data Analysis Read More »

Interpretations of Probability

This time, we examine how different schools of mathematicians and philosophers have interpreted the concept of probability. We consider five different versions.

Classical approach

The earliest version. Thanks to people such as Laplace, Fermat, Pascal, etc, who wanted to explain the principles of games of chance (e.g., gambling). In their definition, for a random trial, the probability of outcomes equals
# of favourable cases / total # of equally possible cases.
This way, a coin has one out of two (1/2) probability to land on a head, and a dice has a one out of six (1/6) chance to land on number 4, etc.

But this leads to a problem, e.g., the probability of rain tomorrow. If the favourable outcome is rain, what are those “equally possible outcomes” – {rain, no rain}? In that case, the probability is
{rain}/{rain, no rain}
is always 1/2, which can not be true!

Logical approach

We know the format of a logical statement – premise leading to conclusions. It defines an argument as one of the two categories – deductively valid or invalid. If the premises entail the conclusion ie.e., true premises guarantee a true conclusion, it’s a valid argument. On the other hand, a conclusion which is not true, even if the premises are all true, is an example of a deductively invalid argument.

What about something in between?
Premise 1: There are 10 balls in a jar: 9 blue and 1 white
Premise 2: One ball is randomly selected
Conclusion: The selected ball is blue

The argument is deductively invalid, but we know the chance of this conclusion being right is high. In other words, the premises partially entail the conclusion. The degree of partial entitlement is probability.

Frequency approach

We all know about the frequency interpretation of probability. Take a coin, toss it and record the sequence of outcomes. Estimate the number of heads over the number of tosses. The long-term ratio or the relative frequency is the probability of heads on a coin toss.

Probability = relative frequency as the # of trials reaches infinity.

But then, what is the probability of a single-case event?

Bayesian approach

What is the probability that I pass today’s exam? Naturally, I don’t have a chance to do a hundred exams and inspect the outcomes. I must express some confidence and give a subjective (gut) feeling. In other words, the probability I assign is a degree of belief.

Note that in the Bayesian approach, we are prepared to ‘update‘ the initial degree of belief based on evidence.

Propensity approach

Propensity is a term coined by the philosopher Karl Popper. Consider the flipping of a fair coin. This philosophy school argues that it’s the physical property or the propensity of the coin that produces a head 50% of the time. And the numerical probability just represents this propensity.

Reference

Interpretations of the Probability Concept: Kevin deLaplante

Interpretations of Probability Read More »

Slippery Slope Fallacy

A popular flawed argument among fearmongers. It’s an argument of connected occurrences of events leading to a disastrous end state.

The schematic view of the slippery slope fallacy is as follows.
1. If A, then B
2. If B, then C
3. If C, then D
4. not-D
Therefore, non-A

Let’s substitute for the steps using a simple example.
If you miss this homework (A), you will fail (B)
If you fail (B), you miss getting admission to college (C)
If you don’t attend a good college (C), you will not get a job (D)
If you do not have a job (D), you will be poor and homeless (E)
Therefore, you must do the homework.

The proponents of the slippery slope fallacy assign certainty for each step. They consider the impact like a domino, where the fall of one guarantees the collapse of the next. This is far from true in real-life situations where there are probabilities. In the above example, even if the chance for each event to happen is high, say 80%, the overall probability of becoming homeless is less than 50% (0.84).

A notorious example from history for this domino theory is the US involvement in the Vietnam War. The argument of President Eisenhower in 1954 was that if Vietnam were allowed to become a communist state, the neighbouring countries and neighbouring regions would become communists, leading to “incalculable consequences to the free world.”

Reference

The Small Sample Fallacy: Kevin deLaplante

Slippery Slope Fallacy Read More »

Uncertainty in a Portfolio

The CEO wants to know the annual budget requirements of 10 of her department heads. Each expects an average of $1 million. Each head decides to present not the average value but a value they are 90% confident they won’t exceed. If they assume their uncertainties are normally distributed, with a standard deviation of 0.1 and submit the figures, what should the CEO allocate for the whole firm?

Step 1: Budget request for a single department
Using the assumption of normal distribution, the budget that is expected to be at the 90 percentile (there is a 90% chance the amount will be within) is $1.13 million. Here is the representation.

Step 2: Budget for the whole company
This is what each head would see. According to this, there are ten requests of $1.13 million or $11.3 million. The CEO uses this information and estimates that the firm’s annual budget has a 90% chance of not exceeding it.

The sum of two independent random variables, X and Y, that are normally distributed, Z = X + Y, is also normally distributed.
X∼𝑁(𝜇X,𝜎X2)
𝑌∼𝑁(𝜇𝑌,𝜎𝑌2)
𝑍=𝑋+𝑌 ∼ 𝑁(𝜇𝑋+𝜇𝑌, 𝜎𝑋2+𝜎𝑌2).

For ten distributions with similar mean and standard deviations, the sum becomes
Z ∼ 𝑁(10𝜇, 10𝜎2)

The CEO will be required to set aside $10.4 million to manage the company within budget at 90% confidence.

Reference

The Flaw of Averages: Sam L Savage

Uncertainty in a Portfolio Read More »