April 2024

Annie’s Table Game – Frequentist vs Bayesian 

See the story and numerical experiments in the previous post. Annie is currently leading 5-3; what is the probability that Becky will reach six and win the game?

Frequentist solution 

Based on the results so far, 3 wins in 8 matches, Beck’s probability of winning is (3/8). That means the probability of Becky winning the next three games (to reach 6 before Annie wins another, which will make her 6) is (3/8)3 = 0.053.

Bayesian solution 

First, we write down the Bayes equation. The probability of B winning the game, given A is leading 5-3, 

\\ P(B|A_{5-3}) = \frac{P(A_{5-3}|B)*P(B)}{P(A_{5-3})}

Let’s start with the denominator. If p represents the probability of Becky winning a game, the probability of a 3-5 or 3 in 8 result is obtained by applying the binomial equation. The denominator is the sum of all possible scenarios (p values from 0 to 1). In other words, The denominator is,

\\ P(A_{5-3}) = \int_0^1 _8C_3 p^3 (1-p)^5

We use an R shortcut to evaluate the integral as the area under the curve using the ‘AUC’ function from the ‘DescTools’ library.

library(DescTools)
x <- seq(0,1,0.01)
AUC(x, choose(8,3)*x^3*(1-x)^5, from = min(x, na.rm = TRUE), to = max(x, na.rm = TRUE)) 
0.1111

And here is the area. 

plot(x, choose(8,3)*x^3*(1-x)^5, type="l", col="blue", ylab = "")
polygon(x, choose(8,3)*x^3*(1-x)^5, col = "lightblue")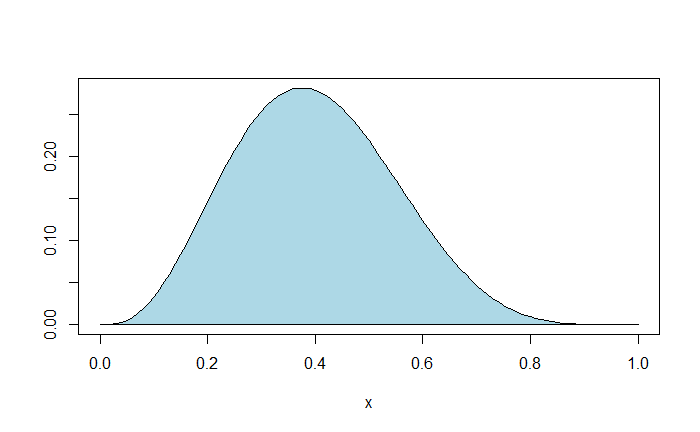

The numerator is the multiplication of the likelihood function with the prior probability of Becky winning three games. We will use a binomial equation as the prior function and p x p x p = p3 as P(B). 

\\ P(A_{5-3}|B)*P(B) = 8C_3 p^3 (1-p)^5 p^3 \\ \\ 8C_3 p^6 (1-p)^5

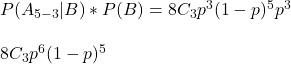
Again, the area under the curve all possible p values (0 -1), 

AUC(x, choose(8,3)*x^6*(1-x)^5, from = min(x, na.rm = TRUE), to = max(x, na.rm = TRUE)) 
0.0101

The required Bayesian posterior is 0.0101/0.1111 = 0.0909

To sum up

The Bayesian estimate is almost double compared to the frequentist. The Bayesian estimate is much closer to the results we saw earlier. Does this make Bayesian the true winner? We’ll see next. 

Annie’s Table Game – Frequentist vs Bayesian  Read More »

Annie’s Table Game

Annie and Becky are playing a game in which the aim is to secure six points first. The Casino randomly rolls a ball onto the table, and the point at which the ball rests is marked. The Casino then rolls another ball at random. If it comes to rest to the left of the initial mark, Annie wins the point; to the right, Becky wins. If Annie is currently leading 5-3, what is the probability that Becky will win the game?

Before we get into statistical methods, we will play the game a million times using R. 

First step: Becky’s chance of winning any game is a random number with uniform probability. If that is the case, the probability of Annie leading 5-3 (or Becky winning 3 out of 8 games) is given by binomial distribution.

beck_pro <- runif(1)
p_5_3 <- dbinom(3, 8, beck_pro)

That gives the probability of having a 5-3 lead for Annie, but that doesn’t mean it will happen for sure. For that to happen, the estimated probability must be greater than a random number between 0 and 1.

  if(runif(1) < p_5_3){
    game_5_3 <- 1
  }else{
    game_5_3 <- 0
  }

Thus, we established instances where Annie was leading 5-3. We will estimate the probability of Becky winning the next three games. 

  if(game_5_3 == 1){
     beck_3_0 <- beck_pro^3
  } else{
     beck_3_0 <- 0
  }

Like we did before, a random number is generated, and if it is less than the probability of Becky winning the next three games, Becky wins; otherwise, Annie wins. 

 if(beck_3_0 == 0){
    win_beck <- "no"
  }else if(runif(1) < beck_3_0){
    win_beck <- "Becky"
  }else{
    win_beck <- "Annie"
  }
  
  })

Calculate this a million times and estimate the proportion of Becky’s win over total wins. 

itr <- 1000000
beck_win <- replicate(itr, {
  beck_pro <- runif(1)
  p_5_3 <- dbinom(3, 8, beck_pro)

  if(runif(1) < p_5_3){
    game_5_3 <- 1
  }else{
    game_5_3 <- 0
  }
  
  
  if(game_5_3 == 1){
     beck_3_0 <- beck_pro^3
  } else{
     beck_3_0 <- 0
  }
  
  
  if(beck_3_0 == 0){
    win_beck <- "no"
  }else if(runif(1) < beck_3_0){
    win_beck <- "Becky"
  }else{
    win_beck <- "Annie"
  }
  
  })

sum(beck_win == "Becky")/(sum(beck_win == "Becky") + sum(beck_win == "Annie"))
0.09057296

Introduction to Bayesian Statistics – A Beginner’s Guide: Woody Lewenstein

What is Bayesian statistics?: Nature Biotechnology,  volume 22, 177–1178 (2004)

Annie’s Table Game Read More »

The Bayesian Runner

Becky loves running 100-meter races. The run timing for girls her age follows a normal distribution with a mean of 15 seconds and a standard deviation of 1s. The cut-off time to get into the school team is 13.5 seconds. If Becky is on the school running team in 100 meters, what is the probability that she runs below 13 seconds?

Without any other information, we can use the given probability distribution to determine the chance of Becky running under 13 seconds.

pnormGC(13,region="below", mean=15,sd=1.,  graph=TRUE)

Since we know she is in the school team, we can update the probability as per Bayes’ theorem. Let’s use the general formula of Bayes’ theorem here:

\\ P(13|T) = \frac{P(T|13)*P(13)}{P(T)}

The first term in the numerator, P(T|13) = 1 (the probability of someone in the team with a cut-off of 13.5 s, given her timing is less than 13s). We already know the second term, P(13), 0.0228.

The denominator, P(T), is the probability of getting on the team, which is nothing but the chance of running under 13.5 seconds. That is, 

pnormGC(13.5,region="below", mean=15,sd=1.,graph=TRUE)

Substituting P(T) = 0.0668 in the Bayes equation,

P(13|T) = 0.0228/0.0668 = 0.34 or 34%

The Bayesian Runner Read More »

Begging the Question

A person new to religion may have questions about the credibility of its belief system. For example, how do I know the way God operates? A person with a Christian belief system will tell you it’s written in the Bible. But how do I know the Bible is telling the truth? I did a search, and one of the results on the validity of the scriptures was the King James Bible online. The first one was:

“2 Timothy 3:16 – All scripture is given by inspiration of God, and is profitable for doctrine, for reproof, for correction, for instruction in righteousness:” 

If you are happy with the answer, like millions of people, you have committed the fallacy of begging the question. Begging the question is a complicated way of describing a circular reasoning, where an argument’s premise assumes the truth of the conclusion.

An argument has three parts:
1. Claim or conclusion – presented upfront
2. Support or evidence – presented to back the claims
3. Warrant or major premise – hidden in the argument but bridges the support to the claim.

Consider the following argument. 

In the fallacy of circular argument, the claim (Bible is telling the truth) takes the evidence (verses from the book of Timothy) from the same book to prove the claim.

Data & Statistics on Autism Spectrum Disorder: CDC

Begging the Question Read More »

Liar Puzzle

Annie says Becky is lying
Becky says Carol is lying
Carol says both Annie and Becky are lying

Who is lying, and who is telling the truth?

  1. If Carol is telling the truth, then Annie (and Becky) is lying. In that case, Becky is not lying (opposite of what Annie, the ‘liar’ said). This is a contradiction. Therefore, Carol is lying.
  2. Since Carol is lying, the person who identified that correctly, Becky, must be telling the truth
  3. If Becky is telling the truth, the first statement is incorrect. Therefore, the person who made the first statement, Annie, is also lying.

Liar Puzzle Read More »

Implied Probabilities and Fractional Odds

If ‘moneyline’ is the term used in American betting, it’s ‘fractional odds’ for the UK. So, for today’s premier league match between Chelsea and Everton, the following are the odds.

HomeDrawAway
14/1910/319/5

This means that if you bet on home, i.e., Chelsea (the match is played in Chelsea’s backyard) and win, you get a profit of £14 for every £19 placed. In other words, you bet £19 and get back £14+£19 = £33.

As before, let’s estimate the implied probability based on the (fair) expected value assumption.
E.V = p x 14 – (1-p) x 19 = 0
14p + 19p – 19 = 0
p = 19/(14 + 19) = 0.576 = 57.6%

As a shortcut: for 14/19, p = 1/[(14+19)/19].

And for the next two
Draw: p (10/3) = 1/[(10+3)/3] = 0.231 = 23.1%
Away (Everton win): p (19/5) = 1/[(19+5)/5] = 0.208 = 20.8%

As expected, the sum of probabilities is not 100% but 101.5%; the house must win.

Implied Probabilities and Fractional Odds Read More »

Implied Probabilities vs Moneyline

We have seen how to interpret the betting odds or moneyline. Take, for example, the NBA odds for one of tonight’s matches.

TeamMoneyline
Washington Wizards+340
Boston Celtics-450

If you place $100 on the Wizards, and they win, you get $440, suggesting a profit of $340 upon winning (and you lose $100 if they lose).
On the other hand, if you bet $450 on the Celtics, and they win, you get $550 (and a loss of $450 if they lose). Your profit for winning is $100.

Implied probability

Let’s apply the expected value concept to this problem. Let p be the probability of winning the prize upon betting on the Wizards. For this to be a fair gamble,
the expected value = p x 340 – (1-p) x 100 = 0
p = 100/440 = 0.227 or 22.7%; this is an implied probability of the bet.

Let q be the probability for the Celtics.
the expected value = q x 100 – (1-q) x 450 = 0
q = 450/550 = 0.818 or 81.8%

Suppose you add the two probabilities, p + q = 104.5%. It is more than 100%, suggesting they are not the actual probabilities (fair odds) of winning the (NBA) game. Since the actual win probabilities of teams must add up to 100%, the sum p + q must be lower than that obtained in the expected value calculations. Therefore, at least one of the expected values must be < 0.

104.5% may be understood as putting $104.5 the money at risk to get $100 back. The difference (104.5 – 100)/104.5 is the bookie’s edge built into the bet.

Implied Probabilities vs Moneyline Read More »

Employee Attrition Dataset

We continue using the ‘tigerstats’ package to analyse the ‘IBM HR Analytics Employee Attrition & Performance’ dataset, a fictional data set created by IBM data scientists and taken from Kaggle. The dataset contains various parameters related to attribution,

Em_data <- read.csv("D:/04Compute/Web/Employee-Attrition.csv")
str(Em_data)
'data.frame':	1470 obs. of  35 variables:
 $ Age                     : int  41 49 37 33 27 32 59 30 38 36 ...
 $ Attrition               : chr  "Yes" "No" "Yes" "No" ...
 $ BusinessTravel          : chr  "Travel_Rarely" "Travel_Frequently" "Travel_Rarely" "Travel_Frequently" ...
 $ DailyRate               : int  1102 279 1373 1392 591 1005 1324 1358 216 1299 ...
 $ Department              : chr  "Sales" "Research & Development" "Research & Development" "Research & Development" ...
 $ DistanceFromHome        : int  1 8 2 3 2 2 3 24 23 27 ...
 $ Education               : int  2 1 2 4 1 2 3 1 3 3 ...
 $ EducationField          : chr  "Life Sciences" "Life Sciences" "Other" "Life Sciences" ...
 $ EmployeeCount           : int  1 1 1 1 1 1 1 1 1 1 ...
 $ EmployeeNumber          : int  1 2 4 5 7 8 10 11 12 13 ...
 $ EnvironmentSatisfaction : int  2 3 4 4 1 4 3 4 4 3 ...
 $ Gender                  : chr  "Female" "Male" "Male" "Female" ...
 $ HourlyRate              : int  94 61 92 56 40 79 81 67 44 94 ...
 $ JobInvolvement          : int  3 2 2 3 3 3 4 3 2 3 ...
 $ JobLevel                : int  2 2 1 1 1 1 1 1 3 2 ...
 $ JobRole                 : chr  "Sales Executive" "Research Scientist" "Laboratory Technician" "Research Scientist" ...
 $ JobSatisfaction         : int  4 2 3 3 2 4 1 3 3 3 ...
 $ MaritalStatus           : chr  "Single" "Married" "Single" "Married" ...
 $ MonthlyIncome           : int  5993 5130 2090 2909 3468 3068 2670 2693 9526 5237 ...
 $ MonthlyRate             : int  19479 24907 2396 23159 16632 11864 9964 13335 8787 16577 ...
 $ NumCompaniesWorked      : int  8 1 6 1 9 0 4 1 0 6 ...
 $ Over18                  : chr  "Y" "Y" "Y" "Y" ...
 $ OverTime                : chr  "Yes" "No" "Yes" "Yes" ...
 $ PercentSalaryHike       : int  11 23 15 11 12 13 20 22 21 13 ...
 $ PerformanceRating       : int  3 4 3 3 3 3 4 4 4 3 ...
 $ RelationshipSatisfaction: int  1 4 2 3 4 3 1 2 2 2 ...
 $ StandardHours           : int  80 80 80 80 80 80 80 80 80 80 ...
 $ StockOptionLevel        : int  0 1 0 0 1 0 3 1 0 2 ...
 $ TotalWorkingYears       : int  8 10 7 8 6 8 12 1 10 17 ...
 $ TrainingTimesLastYear   : int  0 3 3 3 3 2 3 2 2 3 ...
 $ WorkLifeBalance         : int  1 3 3 3 3 2 2 3 3 2 ...
 $ YearsAtCompany          : int  6 10 0 8 2 7 1 1 9 7 ...
 $ YearsInCurrentRole      : int  4 7 0 7 2 7 0 0 7 7 ...
 $ YearsSinceLastPromotion : int  0 1 0 3 2 3 0 0 1 7 ...
 $ YearsWithCurrManager    : int  5 7 0 0 2 6 0 0 8 7 ...

barchartGC

barchartGC(~Gender,data=Em_data)
barchartGC(~Attrition+Gender,data=Em_data, stack = TRUE)

xtabs

xtabs(~Attrition+MaritalStatus,data=Em_data)
         MaritalStatus
Attrition Divorced Married Single
      No       294     589    350
      Yes       33      84    120
xtabs(~Attrition+Gender,data=Em_data)
         Gender
Attrition Female Male
      No     501  732
      Yes     87  150

CIMean

CIMean(~MonthlyIncome,data=Em_data)

ttestGC

ttestGC(~MonthlyIncome,data=Em_data)
Inferential Procedures for One Mean mu:

Descriptive Results:

variable       mean     sd       n          
MonthlyIncome  6502.931 4707.957 1470       

Inferential Results:

Estimate of mu:	 6503 
SE(x.bar):	 122.8 

95% Confidence Interval for mu:

          lower.bound         upper.bound          
          6262.062872         6743.799713      
ttestGC(~Age,data=Em_data)
Inferential Procedures for One Mean mu:

Descriptive Results:

variable  mean     sd       n          
Age       36.924   9.135    1470       

Inferential Results:

Estimate of mu:	 36.92 
SE(x.bar):	 0.2383 

95% Confidence Interval for mu:

          lower.bound         upper.bound          
          36.456426           37.391193

Employee Attrition Dataset Read More »

Goodness of Fit using tigerstats

We have seen how the R package ‘tigerstats’ can help visualise basic statistics. The library has several functions and datasets to teach statistics at an elementary level. We will see a couple of them that enable hypothesis testing.

chi-square test

We start with a test for Independence using the chi-square test. The example is the same as we used previously. Here, we create the database with the following summary.

High SchoolBachelorsMastersPh.d.Total
Female60544641201
Male40445357194
Total100989998395
as_tibble(educ)

The function to use is ‘chisqtestGC’, which takes two variables (~var1 + var2) to test their association. Additional attributes such as graph and verbose yield the relevant graph (ch-square curve) for the P-value and details of the output.

chisqtestGC(~EDU+SEX, data=educ, graph = TRUE, verbose = TRUE)
Pearson's Chi-squared test 

Observed Counts:
             SEX
EDU           Female Male
  Bachelors       54   44
  High School     60   40
  Masters         46   53
  Ph.d.           41   57

Counts Expected by Null:
             SEX
EDU           Female  Male
  Bachelors    49.87 48.13
  High School  50.89 49.11
  Masters      50.38 48.62
  Ph.d.        49.87 48.13

Contributions to the chi-square statistic:
             SEX
EDU           Female Male
  Bachelors     0.34 0.35
  High School   1.63 1.69
  Masters       0.38 0.39
  Ph.d.         1.58 1.63


Chi-Square Statistic = 8.0061 
Degrees of Freedom of the table = 3 
P-Value = 0.0459

Binomial test for proportion

Suppose a coin toss landed on 40 heads in 100 attempts. Perform a two-sided hypothesis test for p = 0.5 as the Null.

binomtestGC(x=40,n=100,p=0.5, alternative = "two.sided", graph = TRUE, conf.level = 0.95)

x = variable under study
n = size of the sample
p = Null Hypothesis value for population proportion
alternative = takes “two.sided”, “less” or “greater” for the computation of the p-value.
conf.level = number between 0 and 1, indicating the confidence interval
graph = If TRUE, plot graph of p-value

Exact Binomial Procedures for a Single Proportion p:
	Results based on Summary Data

Descriptive Results:  40 successes in 100 trials

Inferential Results:

Estimate of p:	 0.4 
SE(p.hat):	 0.049 

95% Confidence Interval for p:

          lower.bound         upper.bound          
          0.303295            0.502791             

Test of Significance:

	H_0:  p = 0.5 
	H_a:  p != 0.5 

	P-value:		P = 0.0569 
binomtestGC(x=40,n=100,p=0.5, alternative = "less", graph = TRUE, conf.level = 0.95)
Exact Binomial Procedures for a Single Proportion p:
	Results based on Summary Data

Descriptive Results:  40 successes in 100 trials

Inferential Results:

Estimate of p:	 0.4 
SE(p.hat):	 0.049 

95% Confidence Interval for p:

          lower.bound         upper.bound          
          0.000000            0.487024             

Test of Significance:

	H_0:  p = 0.5 
	H_a:  p < 0.5 

	P-value:		P = 0.0284

Goodness of Fit using tigerstats Read More »

Probability, Likelihood and tigerstats

This post refreshes the probability vs likelihood concept and presents a few R functions from the tigerstats library. As usual, we begin with a coin-flipping exercise. What is the probability of obtaining 45 heads upon flipping 100 fair coins? A fair coin is one in which the chance of getting heads equals the chance of getting tails: 0.5.

Here is a graphical representation of the ask.

library(tigerstats)
bound <- c(45,45)
pbinomGC(bound,region="between",size=100,prob=0.5,graph=TRUE)

Coin tossing is a discrete event, and the Y-axis represents the probability. The probability of obtaining 45 heads while flipping 100 fair coins is 0.048.

Now, consider a continuous distribution. Suppose the heights of adults are normally distributed in a population with a mean of 175 cm and a standard deviation of 6.5 cm. What is the probability that a random person measures height between 185 and 190 cm?

sample <- c(185,190)
pnormGC(bound=sample,region="between", mean=175,sd=6.5,graph=TRUE)

Notice a few things: the Y-axis is not probability but probability density. The required probability is the area (under the curve) between two values, the height between 185 and 190 cm = 0.0515. In a continuous distribution, where the probability can take every possible value between 0 and 1, getting the chance for precise height (say, 180.0000) does not make sense.

Likelihood

If probability was about getting 45 heads for a coin with p = 0.5 tossed 100 times, the likelihood is the mirror image of that. What is the likelihood of having a fair coin (p = 0.5) if the coin lands 45 heads in 100 tosses?

In likelihood discussions, you have the data, i.e., 45 heads in 100 tosses. The investigator’s task is to find out the coin bias.
The likelihood that it’s an unbiased coin (p = 0.5), given that 45 in 100 landed on heads, is 0.048.
The likelihood that the coin is biased with p = 0.55, given that 45 in 100 landed on heads, is 0.011.
The likelihood that the coin is biased p = 0.4, given that 45 in 100 landed on heads, is 0.048.

Similarly, for heights,
The likelihood of a distribution with mean = 175 cm and a standard deviation = 6.5 cm, given the measured height = 185, is 0.019
The likelihood of a distribution with mean = 180 cm and a standard deviation = 6.5 cm, given the measured height = 185, is 0.046

In summary

Probability is about the chance of data under a given distribution, P(Data|Distribution)

Likelihood is about the distribution for the given data, L(Distribution|Data)

Reference

Probability is not Likelihood. Find out why!!!: StatQuest with Josh Starmer

Probability, Likelihood and tigerstats Read More »