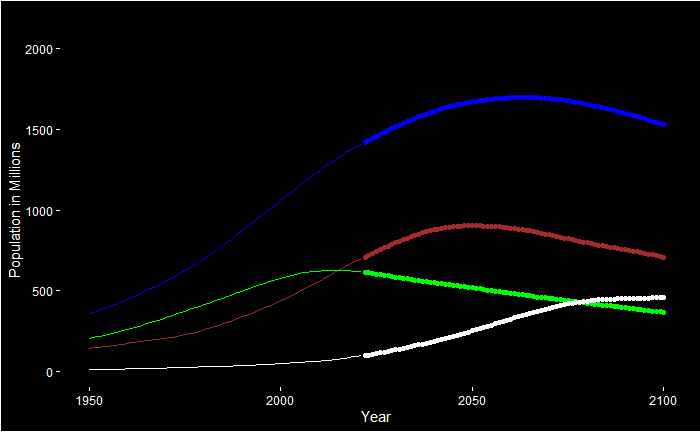
Principal Component Analysis – Building the Case
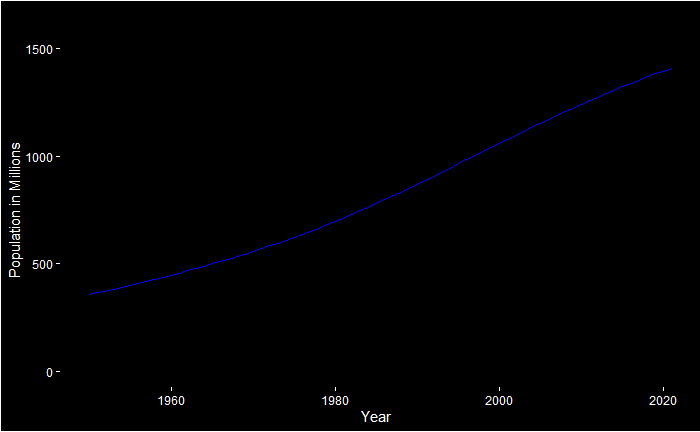
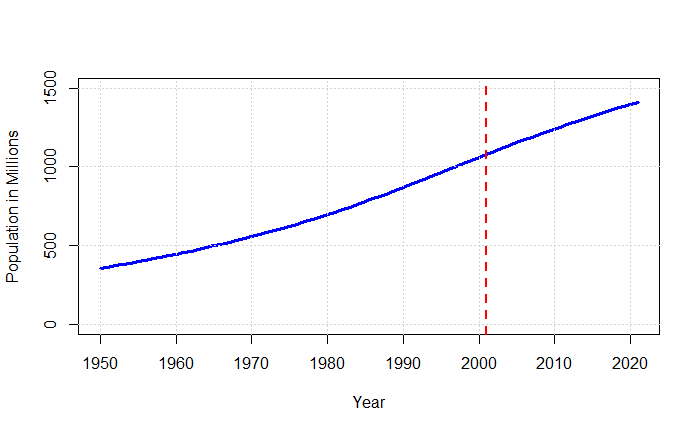
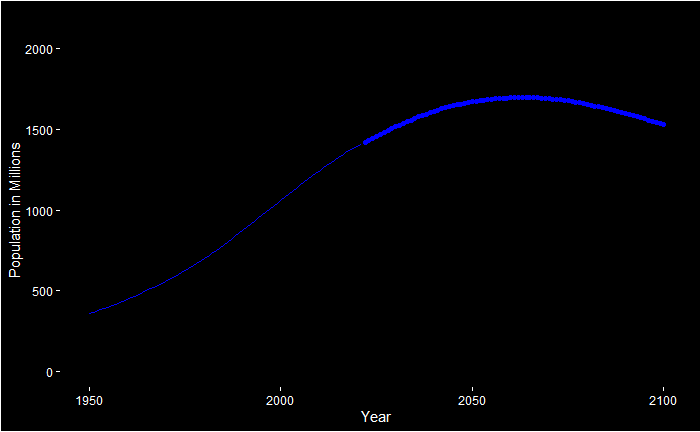
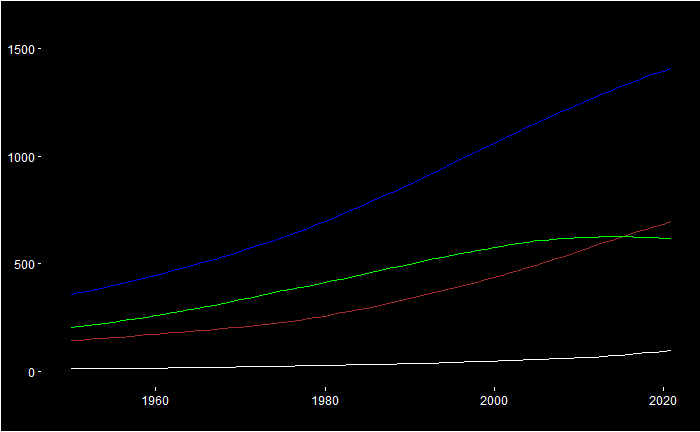
Do you remember the “mtcars” dataset? It’s data collected from the 1974 Motor Trend US magazine and it comprises fuel consumption and ten aspects of automobile design and performance for 32 automobiles (1973–74 models). We’ll use it to explain the concept of principal component analysis or PCA.
If we measure only one aspect, we can present the data on a line plot:
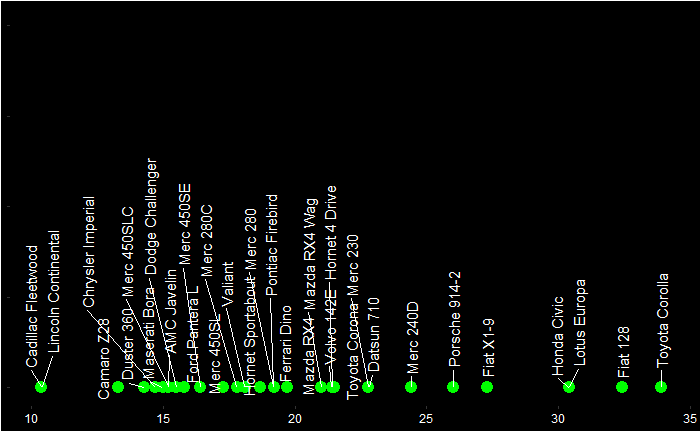
You can see that Toyota Corolla, Fiat 128 etc., are similar to each other, and have relatively higher mileage values, whereas Cadillac Fleetwood and Lincoln Continental have lower.
If we measure two properties, we can present the data in a 2-D graph.
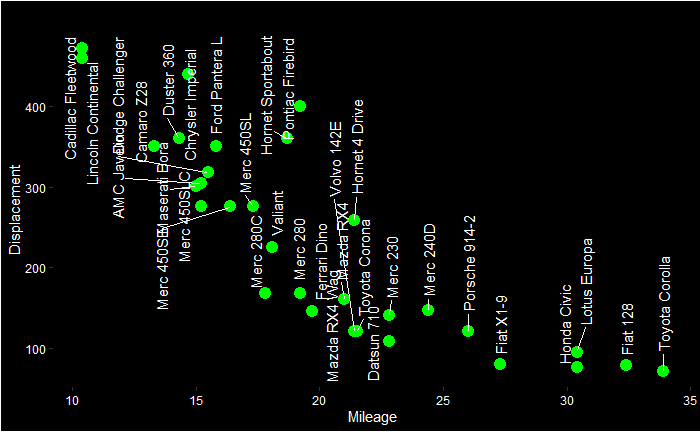
If we measure one more property, we would add one more axis to the graph for a 3-D plot. But what happens if we have four or more parameters? PCA can take four or more measurements and make a 2-D PCA plot.
Principal Component Analysis – Building the Case Read More »