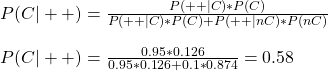April 2022

Riskier Flights

That flight travel is one of the safer modes of transportation is a foregone conclusion. Yet, there seems to be some confusion about the risk of taking flights versus, say, cars. Therefore the comparison requires a reevaluation.

The first question is: what is the right metric to use? Is it the number of fatalities per passenger boarding? Or is it the number of accidents/deaths per boarding? Yet another one is the number of accidents/deaths per passenger-kilometre travelled. Let’s make some (gu)estimates on each of these.

Available data

ItemData
# of flights40 mln (2019)
# aviation incidents125 (2019)
# fatal accidents8 (2019)
# aviation deaths575 (2019)
# passengers 4500 mln (2019)
average trip length2000 km
passenger-km9000 bln (2019)

Calculated quantities

MetricData
Incidents per trip3.13
(per million trips)
Fatal incidents per trip0.2
(per million trips)
Fatality per trip14.4
(per million trips)
Fatality per passenger-km0.06
(per billion-km)
Fatality per passenger0.13
(per million passengers)

Risk of air travel

In my option, the right metric is either the number of incidents per trip or the number of fatal incidents per trip. And probably the difference between road vs air. In air travel, the distance covered or the number of hours in the air are not the prime variable for incidents; riskier parts of a flight are the takeoff and landing, each of which happens once every trip, however brief or lengthy the travel be.

Comparison with the road

So how does it compare with road travel? That is a bit more complex as the data are hard to come by, requiring a lot of assumptions. Also, the risk of road travel has not distributed the way it is for the air. We’ll visit those in another post.

References

[1] http://www.rvs.uni-bielefeld.de/publications/Reports/probability.html
[2] https://economictimes.indiatimes.com/news/politics-and-nation/india-tops-the-world-with-11-of-global-death-in-road-accidents-world-bank-report/articleshow/80906857.cms
[3] https://en.wikipedia.org/wiki/Aviation_accidents_and_incidents
[4] https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries
[5] https://www.icao.int/annual-report-2019/Pages/the-world-of-air-transport-in-2019.aspx
[6] https://data.worldbank.org/indicator/IS.AIR.PSGR
[7] https://en.wikipedia.org/wiki/Aviation_safety
[8] https://accidentstats.airbus.com/statistics/fatal-accidents
[9] https://injuryfacts.nsc.org/home-and-community/safety-topics/deaths-by-transportation-mode/
[10] https://www.sciencedaily.com/releases/2020/01/200124124510.htm

Riskier Flights Read More »

Florida and Sibling Stories

We have seen the girl paradox in one of the older posts. Today we do a series of variations of the problem using Bayes’s equation. Sorry, Bayes-Price-Laplace equation! In a town far far away, every household has exactly two children.

The probability of two girls in a family

\\ P(GG) = \frac{1}{4}

The probability of two girls in a family, if you know, they have at least one girl.
We use the generalised equation here.

\\ P(GG|1G) = \frac{P(1G|GG)*P(GG)}{P(1G|GG)*P(GG) + P(1G|GB)*P(GB) + P(1G|BG)*P(BG) + P(1G|BB)*P(BB)} \\\\ = \frac{1*\frac{1}{4}}{1*\frac{1}{4} + 1*\frac{1}{4} + 1*\frac{1}{4} + 0*\frac{1}{4}} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3}

I guess you don’t need a lot of explanations. B represents a boy, and G represents a girl. The prior probability of each combination, BB, BG, GB or GG, is (1/4); equally likely.

The probability of two girls in a family, if you know, a family has a girl named Florida. Florida is a girl’s name, and let p is the probability of a girl named Florida.

\\ P(GG|F) = \frac{P(F|GG)*P(GG)}{P(F|GG)*P(GG) + P(F|GB)*P(GB) + P(F|BG)*P(BG) + P(F|BB)*P(BB)} \\\\ = \frac{[p(1-p)+(1-p)p+p^2]*\frac{1}{4}}{[p(1-p)+(1-p)p+p^2]*\frac{1}{4} + p*\frac{1}{4} + p*\frac{1}{4} + 0*\frac{1}{4}} = \frac{(2p-p^2)*\frac{1}{4}}{(2p-p^2)*\frac{1}{4} + p*\frac{1}{4}} = \frac{2-p}{4-p}

You may be wondering where that long-expression for P(F|GG) comes from. It’s the total probability of having a girl named Florida, regardless of whether they have already a daughter named Florida. So p(1-p) (the first girl is Florida and the other girl is not), (1-p)p (the second girl is Florida and the other girl is not), and p2 (both girls are Florida).

This is interesting. If the probability of a girl’s name Florida is 1, or every girl is named Florida, then P(GG|F) = (1/3) = P(GG|1G). If the name is rare or close to zero, P(GG|F) becomes (1/2).

Florida and Sibling Stories Read More »

A Laplace Equation Named Bayes

You may be wondering at the title of this post. Well, it is true – it was Laplace who made the Bayes equation. But not the Bayes theorem!

Bayes theorem may have been postulated a few years before Pierre Simon Laplace was born, in 1749. Bayes’ view about probabilities was more conceptual. It was a simple idea of modifying our subjective knowledge with objective information. In more technical language: initial (subjective) belief (guess or prior) + objective data = updated belief. Interestingly, those two words – subjective and belief – made classical statisticians, aka frequentists, mad!

Laplace, unaware of what Bayes had done more than two decades before, had his own ideas about the probability of causes. Eventually, he came up with a theory: the probability of a cause (given an event) is proportional to the probability of the event (given the cause). Note how close he has come to the Bayes formula that we know today.

It took Laplace another eight years or so to learn about Bayes’ idea of a prior, which gave Laplace’s equation the form as we know it. Well, by the name Bayes equation!

A Laplace Equation Named Bayes Read More »

When It’s No Longer Rare

Let us end this sequence of Sophie and her cancer screening saga. We applied Bayes’ theorem and showed that the probability of having the disease is low, even with a positive test result. But the purpose was not to downplay the importance of diagnostics tests. In fact, it was not about diagnostics at all!

Screening a random person

Earlier, we have used a prior of 1.5% based on what is generally found in the population (corrected for age). And that was the main reason why the conclusion (the posterior) was so low. It was also considered a random event. Sophie had no reason to suspect a condition; she just went for screening.

Is different from Diagnostics 

You can not consider a person in front of a specialist as random. She was there for a reason – maybe discomfort, symptoms, or recommendation from the GP after a positive result from a screening. In other words, the previous prior of 1.5% is not applicable in this case; it becomes higher. Based on the specialist’s database or gutfeel, imagine that the assigned value was 10%. If you substitute 0.1 as the prior in the Bayes’ formula, we get about 50% as the updated probability (for the set of screening devices).

Typically, the diagnostic test would have a better specificity. If the specificity goes up from 90 to 95%, the new posterior becomes close to 70%. It remains high, even if the sensitivity of the equipment dropped from, say, 95% to 90%.

When It’s No Longer Rare Read More »

Why Posterior is the New Prior?

So far, we have been accepting the notion that the posterior probability from the Bayes’ equation becomes the prior when you repeat a test or collect more data. Today, we verify that argument. What is the chance of having the disease if two independent tests turned positive? Let’s write down the equation.

\\ P(D|++) = \frac{P(++|D)*P(D)}{P(++|D)*P(D) + P(++|nD)*(1-P(D))}

Since the two tests are independent, and the marginal probability of the two positive tests is similar, we can write P(++|D) as the joint probability, P(+|D)*P(+|D). The same is true for the false positives, P(++|nD). Substituting all of them, we get

\\ P(D|++) = \frac{P(+|D)*P(+|D)*P(D)}{P(+|D)*P(+|D)*P(D) + P(+|nD)*P(+|nD)*(1-P(D))}

P(+|D) is your sensitivity, P(+|nD) is 1 – specificity and P(D) is the assumed prior.

Now, we will go to the original proposition of the posterior becoming the next prior. The probability of having the disease given the second test is also positive is given by

\\ P(D|2nd +) = \frac{P(2nd +|D)*P(D|1st+)}{P(2nd +|D)*P(D|1st+) + P(2nd+|nD)*(1-P(D|1st+))} \\ \\ \text{where, } \\ \\ P(D|1st+) = \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} \\ \\ \text{since these tests are independent}, P(2nd +|D) = P(+|D) \text{. Substituting, } \\ \\ P(D|2nd +) = \frac{P(+|D)*P(D|1st+)}{P(+|D)*P(D|1st+) + P(+|nD)*(1-P(D|1st+))} \\ \\ = \frac{P(+|D)* [ \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} ] }{P(+|D)* [ \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} ] ) + P(+|nD)*(1- [ \frac{P(+|D)*P(D)}{P(+|D)*P(D) + P(+|nD)*(1-P(D))} ] )} \\ \\ \text{expanding and cancelling similar terms,} \\ \\ P(D|2nd +) = \frac{P(+|D)*P(+|D)*P(D)} {P(+|D)*P(+|D)*P(D) + P(+|nD)*(1-P(D))} = P(D|++)

Yes, posterior is the new prior! If you generalise the equation for n number of independent tests,

\\ P(D|+n) = \frac{P(+|D)^n*P(D)}{P(+|D)^n*P(D) + P(+|nD)^n*(1-P(D))}

Why Posterior is the New Prior? Read More »

Equation of Life Revisited

I guess you remember the story of Sophie that we encountered at the start of our journey with the equation of life. She has tested positive during a cancer screening but found that the probability of the illness was about 12% after applying Bayes’ principles. There was nothing faulty about the test method, which was pretty accurate, at 95% sensitivity and 90% specificity. Now, how many independent tests does she need to undertake to confirm her illness at 90% probability?

Assume that her second test was positive: The probability for Sophie to have cancer, given that the second test is also positive,

\\ P(C|++) = \frac{P(++|C)*P(C)}{P(++|C)*P(C) + P(++|nC)*P(nC)} \\ \\ P(C|++) = \frac{0.95*0.126}{0.95*0.126 + 0.1*0.874} = 0.58

The updated probability has become 56% (note we have used 12.6%, which is the posterior of the first examination, as the prior and not the original 1.5%). Applying the equation one more time for a positive (third by now) test, you get

\\ P(C|++) = \frac{0.95*0.58}{0.95*0.58 + 0.1*0.42} = 0.93

So the answer is three tests to get a high level of confidence.

You may recall that the prior probability used in the beginning was 1.5%, based on what she found in the American Cancer Society publications. What would have happened if she did not have that information? She still needs a prior. Let’s use 0.1% instead. Let’s work on the math, and you will find that about 89% probability can reach in the fourth test, provided all are positive. Therefore, an accurate prior is not that crucial as long as you follow up with more data collection, which is the power of the Bayesian approach.

Equation of Life Revisited Read More »

Another Game Behind Closed Doors

We have seen the Monty Hall problem in an earlier post. This time, instead of 3, we have four doors. There is $1000 behind one door, -$1000 behind another (you lose $1000), and two other doors have nothing ($0). Like in the previous game, you choose one door, and then the game host opens a door that contains nothing. You have an option to change to one of the other closed doors now. What will you do?

No Change

In the beginning, before hosts reveals the $0 door, the probabilities are P($1000) = 1/4, P($0) = 1/2 and P(-$1000) = 1/4. The expected return is (1/4) x $1000 + (1/2) x $0 + (1/4) x -$1000 = $0. After the clue, if you still don’t want to change, this remains the case.

Change

Here, we use solution 2, the argument method, of the Monty Hall problem. Before you get the clue, the chance that you chose the $1000 door is 1/4, and that the prize was outside your choice is 1 – 1/4 = 3/4. After the clue, that probability of 3/4 sits behind two doors. In other words, if you shift, the chance of getting $1000 is 3/8. Using similar arguments, we shall see that the chance of losing became 3/8, and for $0 is 1/4. The expected return is (3/84) x $1000 + (1/2) x $0 + (3/8) x -$1000 = $0.

Will you change?

Well, it depends on your risk appetite. The chance of winning and the chance of losing have increased. But the expected returns remained the same, at zero. Or the risk has increased if you shift. If you are risk-averse, stay where you are!

Another Game Behind Closed Doors Read More »

Decisions of groups

Decision-making in groups often suffers from what is known as the Arrow’s impossibility problem. Named after the American Economist Kenneth Arrow, this theory says that if a decision is made by a group of individuals who are not run by a dictator, through sincere voting, they may reach a state of non-transitive preference even if they are all rational.

The statement sounds very complicated. Let’s look at each of those words. First, something about the group – they are free and have clear preferences. The second one is non-transitive preference. To understand this, we must understand what transitive preferences are.

Transitive preference

Rational decision-makers have transitive preferences. That means if a decision-maker prefers A over B, then B over C, it must be that she prefers A over C. A sort of mathematical consistency. But this is so if the decision-maker is one person. What can happen if there is more than one? Take this example of three members of a local committee, Mrs Anna, Mr Brown and Miss Carol. The following represent their choices on what they prefer to build for the local community this year.

AnnaBrownCarol
First PreferenceSchoolLibraryPlayground
Second PreferenceLibraryPlaygroundSchool
Third PreferencePlaygroundSchoolLibrary

The committee votes for pair-wise comparison. The first is school vs library. Anna and Brown vote for their first choices, the school and the library, respectively, and Carol for school (because the library is her least preferred ). The school won 2-1.

The school vs playground happens next. The votes go through a similar process, and the playground wins this time, thanks to Mr Brown; the school was his least preferred option.

You may conclude that the committee should build a playground because it beat the school that defeated the library. But before that, they have to do the final voting- the library vs the playground. Since it was sincere voting, as you expected, the library won by 2 to 1 as Anna, the decider, broke the tie. And we ended up in a non-transitive situation.

Decisions of groups Read More »

Bayesian vs Frequentist

There are two main perspectives in statistical inference. They are Baysianism and frequentism. So what are they? Let’s understand them using a coin-tossing example. It goes like this. What is the probability of getting a head if I toss a coin?

Bayesian first assumes, then update

Well, the answer depends on whom you ask! If you ask a Baysian, she will start the following way: a coin has two sides – a head and a tail. Since I don’t know whether the coin is fair or biased, I assume in favour of the former. In that case, the probability is (1/2), and then, depending on what happens, I may update my belief!

Frequentist first counts, then believe

You ask the same question to the frequentist, and she will hesitate to assume but will ask you to do the tossing a hundred times, count them and then estimate!

How can one event has two different chances?

The toss just happened, but the outcome is hidden from your sight. The question is repeated: what is the probability that it is a head? The Bayesian would still say it is (1/2). The frequentist’s perspective is different. The coin is already landed, and there is no more probability: it has to be either a head or a tail. If it is a head, the answer is 100%, but if it is a tail, the answer is 0%!

Who is right?

If you recall my old posts, I have used Bayesian mostly in calculations but frequentist for explaining things. One classic example is the weather forecast. The easiest way we can understand a 40% probable rain tomorrow is if I tell you that when such weather conditions happened in the past 100 occasions, it rained in 40 of them. And you are happy with the explanation. But in my weather model, I may have used 0.4 as a parameter and depending on what happened tomorrow (actually, it rained), I may have updated my model like a true Bayesian.

Bayesian vs Frequentist Read More »

Confirmation Pull

Most of us acknowledge the need to be objective; in what we believe or what we decide. Yet, we find it tough to follow the path of true objectivity as the pull from the value system is so strong. And we settle for results that fit with our current ideas.

My-side objectivity

And that is confirmation bias. It is a state in which individuals will search, accept and interpret information that favours their existing beliefs. Traditionally it required active selection from the individual, be in the newspaper she chooses, the books she reads etc.

Filter bubble

Naturally, the bias also requires us to ignore the evidence that does not fit our liking. And that used to be a difficult job. But that is past. With the introduction of filter bubbles or those algorithms that choose the feed for you, confirmation has reached a different level. The algorithm practically takes the decision, on your behalf, on what to click on and what not to.

Confirmation Pull Read More »