Colorectal Cancer and Meat-Eaters
In 2015, the World Health Organisation (WHO) added processed meat to group 1 carcinogens (carcinogenic to humans). It was based on a report published in October 2015 by the International Agency for Research on Cancer (IARC). The list contains, among others, tobacco, gamma rays, benzene, and asbestos!
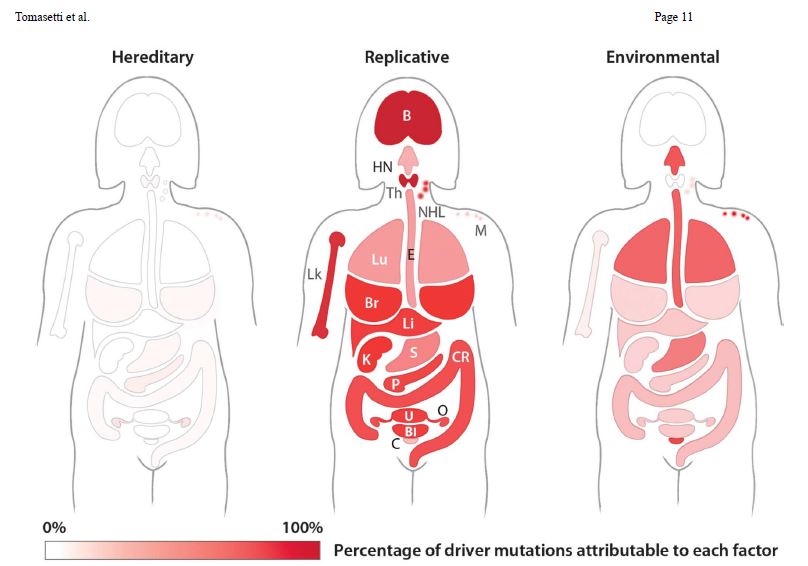
IARC report scanned through scientific literature and concluded that there was evidence that processed meat could cause cancer in humans. The experts concluded that each 50-gram portion of processed meat eaten daily increases the risk of colorectal cancer by 18%.
Lost in Statistics?
As usual, the media went overboard with the news, some of them to the extent:
“BACON, HAM, SAUSAGES HAVE SAME CANCER RISK AS CIGARETTES: WHO REPORT” (First Post)”
Is it true that processed meat is as dangerous as smoking cigarettes? Are all items on the list have the same risk? Does 18% cancer risk mean 1 in 6 of the meat-eaters die of colorectal cancer?
Absolute and Relative Risks
The above was a classic case of people misinterpreting relative and absolute risks. 18% in the present case represented a relative risk – an increase of risk compared to the risk of getting colorectal cancer among non-processed meat-eaters. To understand relative risk, you first need to know the base or the absolute risk on which it was calculated. And if it is a low base, expect a high percentage for every unit change, like the GDP growth rates of smaller developing economies vs big, well-developed ones.
So, what is the absolute risk or the proportion of patients in the population? As per the American Cancer Society, the lifetime risk of developing colorectal cancer is about 1 in 23 (4.3%) for men and 1 in 25 (4.0%) for women. For simplicity, let’s take 5%; 18% of 5% is 0.009% or about 1 in 100. The bottom line is:
5 in 100 people can get colorectal cancer in the US, and if all of them start eating 50 g of processed meat every day, the risk increases to an additional person!

This also answers the remaining doubt on the group 1 list: Not all carcinogens in the WHO list have the same risk.
IARC Report on Processed Meat
Known Carcinogens: Cancer.org
Carcinogenicity of Processed Meat: The Lancet Oncology
How common is colorectal cancer: cancer.org
Colorectal Cancer and Meat-Eaters Read More »