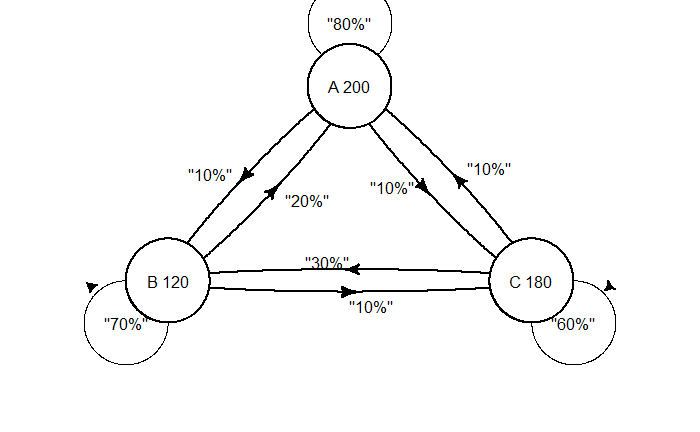
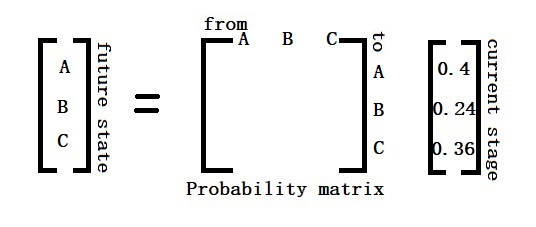
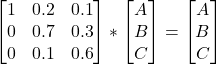Hidden Markov Model
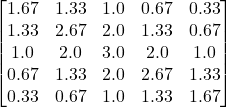
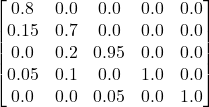
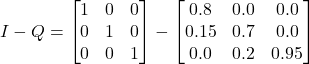
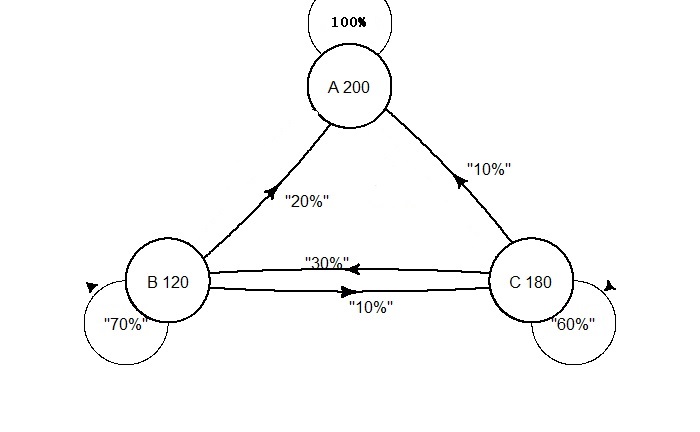
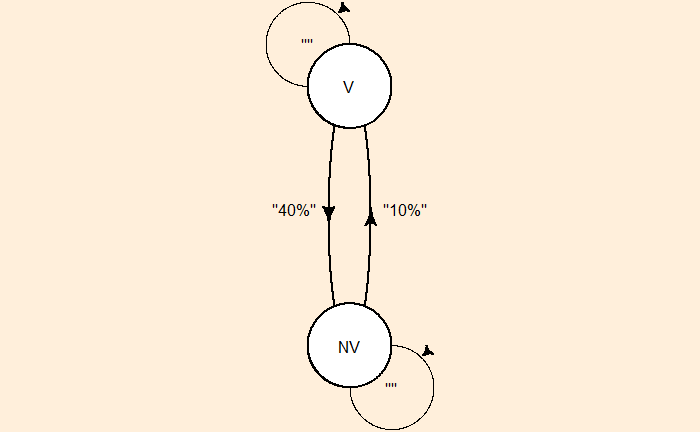
We have seen how states move from one to another and the translation probabilities. It models a sequence in which the probability of the following (n+1) event depends only on the state of the previous (n) event. That is normal, Markov, where we can see the states. Imagine we can’t directly observe the states but only observe some indications. That is hidden Markov.
An often-used example is observing people’s attire and estimating if it’s sunny or rainy.
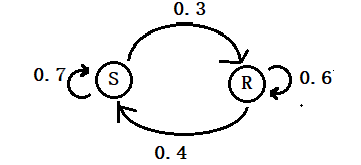
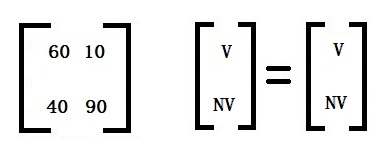
If it rains today, there is a 60% chance it will rain the next day and a 40% chance it will be sunny.
If it’s sunny today, there is a 70% chance it will be sunny tomorrow, and 30% will be rainy.
But you can’t observe that. All you see is people wearing a raincoat or normal clothes.
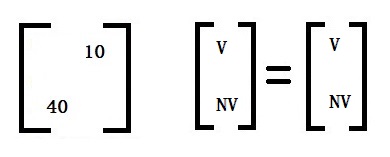
If it rains, there is a 60% chance you will see people wearing raincoats and 40% normal clothes.
If it’s sunny, there is a 90% chance you will see people wearing normal clothes and 10% rain clothes.

Hidden Markov Model Read More »