Life

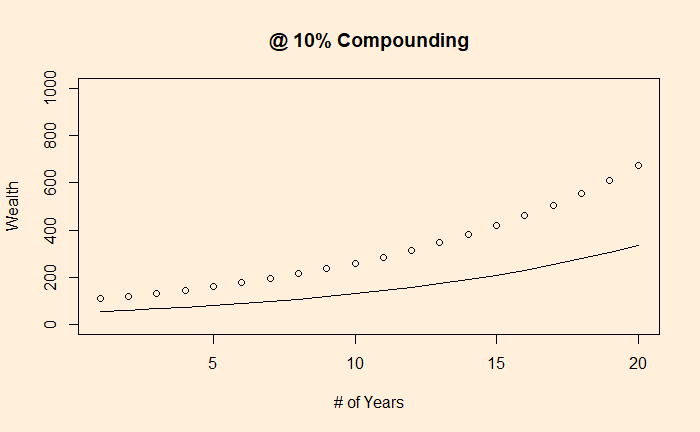
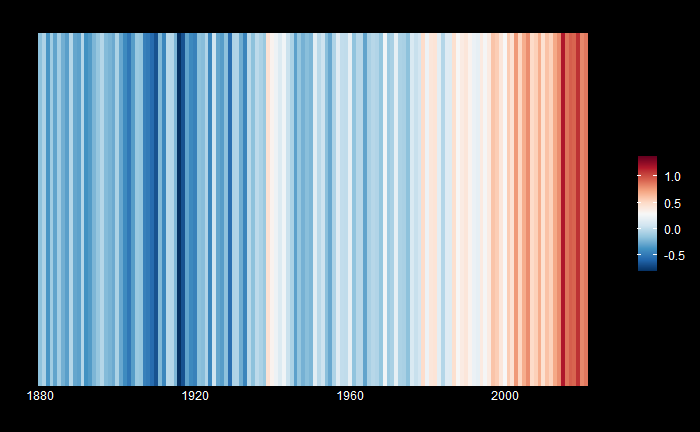
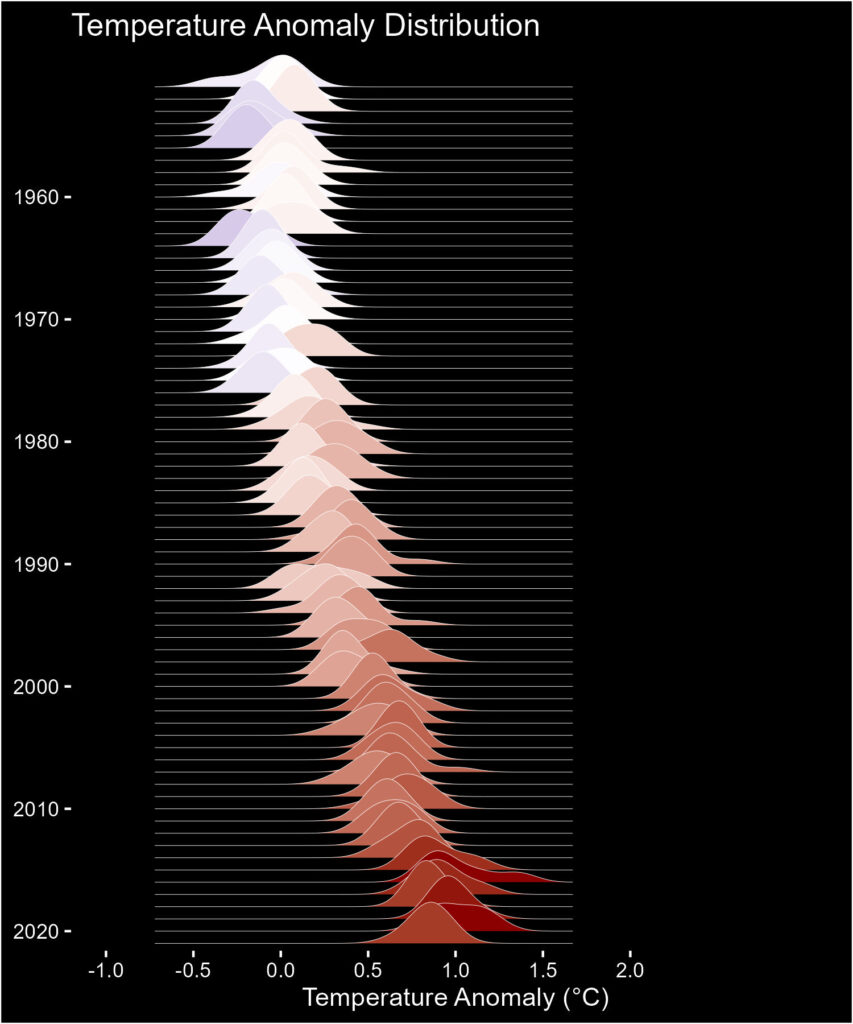
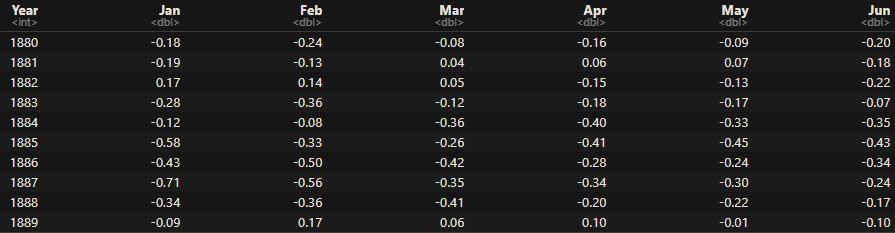
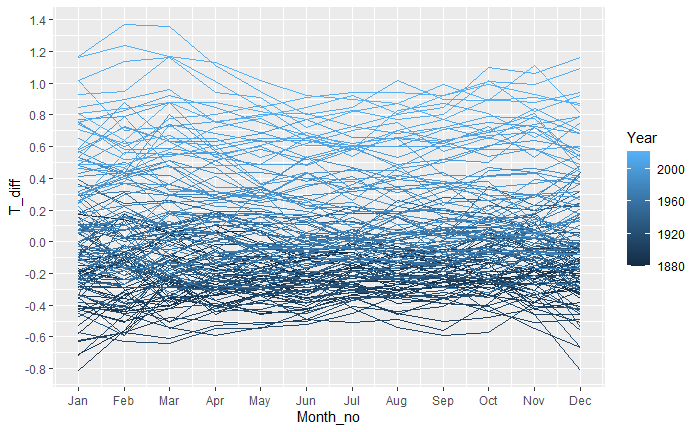
Bayes’ Theorem – Graphical Representation

Here is a graphical illustration of Bayes’ theory. We use the old example of Steve, “the shy and withdrawn”.

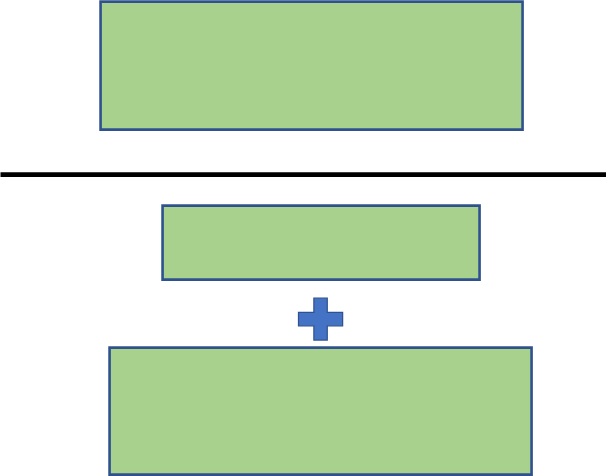
The colour orange represents the number of librarians, and the light blue the farmers.

From the relative sizes of the rectangles, you make out that the number of farmers is more than the number of librarians. This, we call, the prior information.

Let’s assume that 80% of the librarians are shy and withdrawn, and only 25% of the farmers possess those characteristics. The following picture, green representing shyness, is more or less that.

Now, here is the question: when you see a random shy and withdrawn person, where do you likely to classify him, given you have two choices – librarian or farmer?

Well, likely in the rectangle on the left, which comes from the farmer group! And if you want a precise probability, here is the math below:

Bayes’ Theorem – Graphical Representation Read More »

The Net Present Value

Future Value

How much money will I have ONE year from today if I invest 100 dollars at an interest rate of 10%? Here, 10% is the annual return. The answer is 100 + 10% of 100 = 100 + 100 x 10% = 110. How much money will I have two years from now if I invest 100 dollars today at the same rate of return?

Value at the end of year 1 = 100 + 100 x 10% = 100 x (1 + 10%)
Value at the end of Year 2 = [100 x (1 + 10%)] + [100 x (1 + 10%)] x (1 + 10%) = 100 x (1 + 10%)2.
So, in general, the future value of P at the end of n years, at a rate of return of r, is:

FV = P x (1 + r)n

Present Value

Let’s ask the question in reverse. How much money should I invest to get 110 dollars in one year from today at a rate of return of 10%? We know that intuitively – it is 100. Formally, we get it by dividing 110 by (1 + 10%). By the way, 10% equals 0.1 (110/1.1 = 100). So the present value of 110 one year from now is 110 / (1 + 0.1). If we extend this further, the present value of C, n years from today, at a rate of return of r, is

PV = C/(1+r)n

Net Present Value

What is the present value (PV) of the future benefits that will happen in the following manner?

Year 1 = 200
Year 2 = 200
Year 3 = 200
Year 4 = 200

That must be PV of year 1 benefit + PV of year 2 benefit + PV of year 3 benefit + PV of year 4 benefit.

200/(1+0.1) + 200/(1+0.1)2 + 200/(1+0.1)3 + 200/(1+0.1)4 = 181.82 + 165.29 + 150.26 + 136.60 = 633.97.

The story is not over yet. What if I need to invest 500 dollars today to get the above benefits (200 dollars every year for 4 years)? Is it a good deal or a bad deal?

To get the answer, you estimate the present value of the future cash flows and subtract what is required to pay today. That is 633.97 – 500 = 133.97. Not bad. It is the net present value of this business.

The underlying principle behind these calculations is known as the ‘time value of money‘.

The Net Present Value Read More »

Temperature Anomaly – Warming Stripes

We have seen the spiral plot and ridgeline plot visualising the temperature anomaly (compared to the 1961-80 average). Today, we make another fancy plot – Warming Stripes – using R (again, courtesy: Ed Hawkins of the University of Reading). The data used here is the same as that we described in an earlier post.

c_data %>% ggplot(aes(x = Year, y = 1, fill = T_diff)) +
geom_tile()+
scale_y_continuous(expand = c(0, 0)) +
            scale_fill_gradientn(colors = rev(brewer.pal(11, "RdBu")))+
            guides(fill = guide_colorbar(barwidth = 1))+
            labs(title = "",
            caption = "")+
            theme_minimal() +
            theme(axis.text.y = element_blank(),
                       axis.line.y = element_blank(),
                       axis.title = element_blank(),
                       panel.grid.major = element_blank(),
                       legend.title = element_blank(),
                       axis.text.x = element_text(vjust = 3),
                       panel.grid.minor = element_blank(),
                       plot.title = element_text(size = 14, face = "bold"),
                       panel.background = element_rect(fill = "black"), 
                       plot.background = element_rect(fill = "black"),
                       axis.text = element_text(color = "white"),
                       legend.text = element_text(color = "white")
                       )

Temperature Anomaly – Warming Stripes Read More »

IESDS -The Cards Game

Amy and Becky are playing a game. Six cards – numbered 1 through 6 – are placed face down on the table. The cards are shuffled, and each one takes a card at random. The person with the higher number wins. Amy looks at her card and finds it is #2. Becky looks at hers and asks if Amy wants to trade her card. What should Amy’s response be? Note both players are rational.

If Becky had a 6, she wouldn’t ask for a trade, as #6 is guaranteed to win. If she had #5, the only card she benefits from is #6, something Amy would never trade. That eliminates #5 and #6 from the game. By extending the logic, 4 and 3 are also eliminated. That leaves #1 something Becky is happy to offer, but Amy will never accept.

So Amy’s answer to the call is a NO.

These types of games are known as the Iterated Elimination of Strictly Dominated Strategies (IESDS).

IESDS -The Cards Game Read More »

Temperature Anomaly – The Ridgeline plot

We have seen the temperature anomaly distribution visualised through a spiral plot. This time it’s another cool one – the ridge plot.

library(tidyverse)
library(ggridges)

c1_data <- c_data %>% group_by(Year) %>% mutate(T_av = mean(T_diff))

c1_data %>% filter(Year > 1950 & Year < 2022) %>% 
  ggplot(aes(x = T_diff, y = factor(Year, levels = seq(2021, 1950, -1)), fill = T_av )) +
  geom_density_ridges(bandwidth = 0.1, scale = 4, size = 0.1, color = "white") +
  scale_fill_gradient2(low = "darkblue", mid = "white", high = "darkred", midpoint = 0, guide = "none") +
  coord_cartesian(xlim = c(-1, 3)) +  
  scale_x_continuous(breaks = seq(-1, 2, 0.5)) +
  scale_y_discrete(breaks = seq(1950, 2020, 10)) + 
  labs(y = NULL, x = "Temperature Anomaly (\u00B0C)", title = "Temperature Anomaly Distribution") +
  theme(text = element_text(color = "white"), 
        panel.background = element_rect(fill = "black"), 
        plot.background = element_rect(fill = "black"),
        panel.grid = element_blank(),
        axis.text = element_text(color = "white"),
        axis.ticks = element_line(color = "white"))

For the data and clean-up, see the earlier post.

Ridgeline plot in R with ggridges: Riffomonas Project

Temperature Anomaly – The Ridgeline plot Read More »

The Climate Spiral – The Spiral with Plotly

In the last post, we initiated the plotting of the abnormal temperature differences over the years (from the standardised values) thought to have been arising out of global warming. Today, we will build the famous spiral plot to visualise it.

First, we transform the data to polar coordinates.

c_data <- c_data %>% select(Year, all_of(month.abb)) %>% 
  pivot_longer(-Year, names_to = "Month", values_to = "T_diff") %>%
  mutate(Month = factor(Month, levels = month.abb)) %>%
  mutate(Month_no = as.numeric(Month), radius = T_diff + 1.5, theta = 2*pi*(Month_no-1)/12, x = radius * sin(theta), y = radius * cos(theta), z = Year)

The input (the original table) and the output (the transformed table) are presented below.

Plotly

Plotly is an open-source graphing library, which also has one for R (plotly).

plot_ly(c_data, x = ~x, y = ~y, z = ~z, type = 'scatter3d', mode = 'lines',
        opacity = 1, line = list(width = 6, color = ~T_diff, reverscale = FALSE))

The Climate Spiral – The Spiral with Plotly Read More »

The Climate Spiral

Let’s construct a visualisation of global temperature change – from 1880 – similar to what the British climate scientist Ed Hawkins did. The data used in the exercise has been downloaded from the GitHub channel of Riffomonas. He tabulated the deviation in the annual global mean from the data normalized between the temperatures 1951 – 1980.

The first step is to pivot the data into the following format:

c_data <- read.csv("./climate.csv")

c_data <- c_data %>% select(Year, all_of(month.abb)) %>% 
  pivot_longer(-Year, names_to = "Month", values_to = "T_diff") %>%
  mutate(Month = factor(Month, levels = month.abb)) %>%
  mutate(Month_no = as.numeric(Month))

Next, we plot the data we built.

c_data %>% ggplot(aes(x = Month_no, y = T_diff, group = Year, color = Year)) +
  geom_line() + 
  scale_x_continuous(breaks = 1:12, labels = month.abb) +
  scale_y_continuous(breaks = seq(-2, 2, 0.2)) +
  coord_cartesian()

Add a line to change to polar coordinates.

c_data %>% ggplot(aes(x = Month_no, y = T_diff, group = Year, color = Year)) +
  geom_line() + 
  scale_x_continuous(breaks = 1:12, labels = month.abb) +
  scale_y_continuous(breaks = seq(-2, 2, 0.2)) +
  coord_polar()

Climate data: Riffomonas

Riffomonas Project: Youtube

Climate spiral: Wiki

The Climate Spiral Read More »

An Ocean Full of Bombay Duck

Here is a story of the survival of the fittest. It seems it is caused by global warming or some other confounding factor. A recent publication by Kang et al. in “Environmental Biology of Fishes” tells a curious – potentially scary – case of things to come.

The team noticed a sudden spike in a particular variety of fish off the coast of southeast China. This weirdly named fish, the Bombay Duck, has had a ten-fold population growth in the last decade. Bombay Duck (Harpadon nehereus) is fish that can survive a low Oxygen environment due to a high (about 90%) water content in its tissues.  

So scientists postulate that as the water temperature rises, thanks to global warming, the dissolved oxygen levels in the water drop, and makes the lives of the indigenous fish species in danger, leaving only those species that can thrive under these conditions to multiply in numbers. So a fish that did not exist in the national statistics as an independent species until recently suddenly becomes a dominant variety.

Increase of a hypoxia-tolerant fish: Environmental Biology of Fishes

An Ocean Full of Bombay Duck Read More »

Einstein’s 10% Brain

Make a guess: how much brain did Einstein use? Then, how much does an average human use? Here is a clue, Einstein used the same quantity as most of us use – 100%. But, many of us believe we don’t use all of it and can improve its utilisation through regular training.

As per a survey made by Dekker et al., 48% of teachers in the UK and 46% in the NL believed in this myth. Interestingly, people maintain this belief despite their knowledge that even a tiny brain injury can inflict significant impairment on human functions.

Myths such as these appeal to us because we know the human potential, like memory, may be enhanced and attribute providing some ‘intelligence’ is the only function of the brain. The brain does a lot more than this. And seats for all body functions – vision, hearing, smell, language, number, touch, motor functions, tear production, blinking, blood flow, coughing, and countless others – are placed all over it.

References

Neuromyths in education: Prevalence and predictors of misconceptions among teachers, Front. Psychol., 18 October 2012
10 Percent Brain Myth: Wired
Do People Only Use 10 Percent of Their Brains?: Scientific American

Einstein’s 10% Brain Read More »