Decision Making

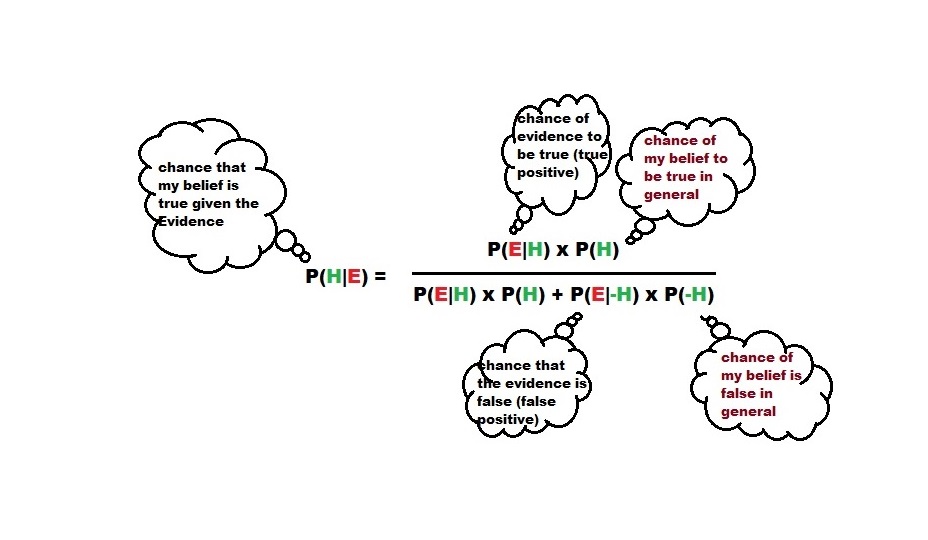
Expected Utility Model

To understand the expected utility theory, you first need to know the expected value theory. Suppose I give you this choice. If there is a 100% chance of getting 100 dollars vs a 20% chance of getting 1000 dollars, which one will you choose?

The expected value (EV), which comes from statistics, is the value multiplied by its respective probability and summed over all possible outcomes. So, for the first choice it is: 100 (dollars) x 1 (sure chance) + 0 (dollars) x 0 (no chance). For the second choice, it is 1000 x 0.2 + 0 x 0.8 = 200. Therefore the expected value of the second is double. So shall I go for the second?

That decision depends on risk and utility

The answer is no more straightforward. EV has given you the limit in terms of statistics, that the second choice yields twice the cash, but your decision follows your risk appetite. It is where the expected utility model comes in. The formula now is slightly different: instead of value, we use utility. So what is utility? The utility is the usefulness of the value.

Suppose you badly need 100 dollars, and anything higher is ok but not going to make a difference. Your utility of money might look the following plot.

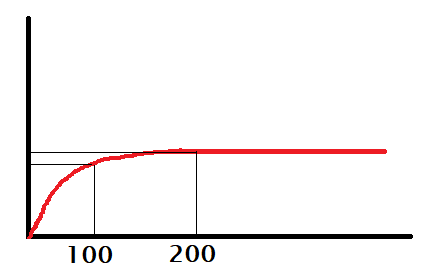
You may call her someone who desperately needs 100 bucks or a risk-averse person.

On the other hand, imagine she desperately needs 1000 dollars. In such a case, the person will gamble for 1000 bucks even when the chance of winning is only 20%. She is either a risk-lover or has no use for anything short of 1000.

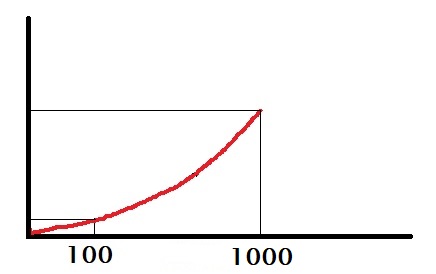
Expected utility model

The expected utility (EU) of the first and the second choices are respectively:
EU1 = U(100) x 1 + U(0) x 0
EU2 = U(1000) x 0.2 + U(0) x 0

In other words, the utility function depends on the person. Suppose, for a risk-averse, it is a square root, and for a risk-lover, it could be a square. Let’s see what they mean.

\\ \text{\bf{for the risk-averse}}, \\ \\ EU1 = \sqrt{100} * 1 + 0 = 10\\ \\ EU2 = \sqrt{1000} * 0.2 + 0 = 6.32\\ \\ EU1 > EU2 \\ \\ \text{\bf{for the risk-lover}}, \\ \\ EU1 = 100^2 * 1 + 0 = 10,000\\ \\ EU2 = 1000^2 * 0.2 + 0 = 200,000\\ \\ EU2 > EU1

Expected Utility Model Read More »

Framing the Risk

We are back with Tversky and Kahneman. This time, it is about decision making based on how the risk appears to you. There is one problem statement with two choices. Two groups of participants were selected and given this but in two different formats.

Here is the question in the first format: imagine that the country is bracing for a disease that can kill 600 people. Two programs have been proposed to deal with the illness – program 1 can save 200 people, and program 2 gives 1/3 probability to save all and 2/3 chance to save none. Which of the two do you prefer? 72% of the people chose program 1.

The second group of participants was given the same problem with different framing. Program 3 will lead to 400 people dying, and program 4 has a 1/3 probability that none will die and 2/3 probability that all will die. 78% of the respondents chose program 4!

Risk aversion and risk taking

Identical problems, but the choices are the opposite! The first case sounded like saving lives, and the players chose what appears to be a risk-averse solution. In the second case, the options sounded like losing lives, and people were willing to take the risk and went for the probabilistic solution.

Tversky, A.; Kahneman, D., Science, 1981, 211, 453

Framing the Risk Read More »

Top Risks Lead to Top Priorities

What should be our top priority in life? Well, it depends on the top risks in life. Depending on whom you ask this question, the answer may vary.

Top priorities

I suspect risk to life comes first. What else can come closer or even be ranked higher? To a large section of the world, it could simply be getting out of poverty. It can be so powerful that individuals may even risk their lives to achieve it for their families and future generations at least. Here, I assume that, at least for the people who read this post, the risk to life is the top one.

Top risks to life

What is the top risk to life? It could be diseases, accidents, extreme weather events, wars, terrorist attacks, etc. Let’s explore this further. According to the World Health Organization (WHO), diseases are the top 10 causes of death and are responsible for 32 out of the 56 million deaths in a year. That is about 60%, according to the 2019 data. And what are they?

Noncommunicable diseases occupied the top seven spots in 2019. Yes, that will change in 2020 and 21, thanks to the COVID-19 pandemic. Deaths due to the current pandemic can reach the top three in 2021, but getting into the top spot is unlikely, at least based on the official records.

The Oscar goes to

The unrivalled winner is cardiovascular diseases (CVDs) – heart attacks and strokes – which cost 18 mln lives in 2019. The risk factors include unhealthy diets, physical inactivity, smoking, and the harmful use of alcohol. And an early warning to watch out for is high blood pressure.

There are three ways to manage the top risk: 1) medication for blood pressure management, 2) regular exercise, and 3) getting into the habit of a healthy diet.

Top 10 causes of death: WHO

Cardiovascular diseases: WHO

Top Risks Lead to Top Priorities Read More »

Risk Perception

Estimation of risk is a very desirable quality to have because it can improve survival rates. Earlier, we have seen the definition of risk as the product of probability and impact. But for most people, it is something far more intuitive and personal. Risk perception, as they are called, may come from recent experiences, news headlines or simply from the lack of knowledge of something. One dominant example is the perception that people live more risky life today than in the past. Data suggest this is incorrect.

Incorrect estimation of risk comes from our mind’s inability to quantify probabilities. That is why when asked about the risk of an even, experts looks at the past (annual incident rate), whereas people consider the future (catastrophic potential). An example is how laypeople perceive the risk due to nuclear power (very high) versus what the experts’ estimate (one of the safest energy technologies)! Wikipedia reports about 30 incidents related to radiations in history, and the deaths were in single digits in 21 of them. Now compare that with a million annually due to coal!

Slovic, Perception of Risk
List of nuclear and radiation accidents
Health and environmental impact of the coal industry

Risk Perception Read More »

420 Remaining in the Bank

Here is an update on the global carbon dioxide (CO2) situation. If you need a background on the topic, you may go to my previous posts on this topic. The world needs to restrict the average temperature rise, from the pre-industrial level, to below 1.5 oC to avert catastrophic climate changes. For simplicity, take 1850 as the start of the counting. 1.5 oC corresponds to a median concentration of CO2 of about 507 ppm (parts per million) in the atmosphere (425-785 ppm at 95% confidence range).

From these numbers, one can estimate the quantity of CO2 we could throw into the atmosphere before it crosses the critical concentration. The maximum remaining quantity of CO2 is known as the Carbon Budget.

Now the numbers: Based on the latest estimate at the beginning of 2022,

ItemQuantityUnit
Carbon Budget420GtCO2
CO2 Concentration414.7ppm
Global anthropogenic CO2 emissions
(2021)		39.4GtCO2
Global fossil CO2 emissions
(2021)		36.4GtCO2
Gt = Gigatonne = billion tonnes; anthropogenic = originating from human activity; 39.4-364. = 3GtCO2 comes from land usage

Spending Wisely

At the current rate, the budget will be over by 2032! There is a resolution from the global fraternity to reduce the net CO2 emission to zero by 2050. If we trust that commitment, one can draw spending scenarios to reach the target. If we spend the remaining 420 Gt in equal chunks, we can do it by spending 15 Gt every year until 2050 and put a hard brake, which is not practical, given the present lifestyle of 36.4 Gt/yr. Another scenario is by reducing 8% every year. Notice that an 8% yearly reduction corresponds to halving every nine years. In other words, the spending in 2030 has to be half of what we did last year.

And How are we doing?

Nothing to cheer about (so far). The emission figures from the last three years have been:

YearTotal CO2 Emitted
(GtCO2)		at 8% reduction
(GtCO2)
201936.736.7
202034.833.8
202136.431

Since we know the real reason for the decline in 2020, the global shutdown due to pandemic, the 8% reduction remains a project without any evidence of progress.

CO2 at 1.5 oC: UK Met office
Carbon Budget Preliminary Data: ESSD

420 Remaining in the Bank Read More »

Expert’s Curse 3: Illusion of Objectivity

A study in 1977 ‘found’ that more than 90% of educators consider themselves above-average teachers. As per the study by Swedish psychologist Ola Svenson (1981), 88% of the Americans and 77% of the Swedes were in the ‘top half’ for driving safely. In another study conducted in 2017, experts agreed (71%) that cognitive bias is a concern in forensics, but only 26% thought that it affected their judgement!

The accounts mentioned above are examples of the illusion of objectivity. It arises from the belief that one understands the world better by their perceptions. You see a lot of it in politics, art and sports. Two prominent examples are the heavy influence of political partisanship in the actions of public policy experts and economics.

Expert sports analysts, especially those coming from the sports after retirement or those who regularly associate with the superstars, often lose their objectivity by being gravitated by the stardom. Remember those heated discussions between Steven A and Max Kellerman – the eternal tussle of adulation versus statistics?

[1] Patricia Cross, New Directions for Higher Education, 17, Spring 1977
[2] O. Svenson, Acta Psychologica 47 (1981) 143-148
[3] Kukucka et al., Journal of Applied Research in Memory and Cognition, 2017

Expert’s Curse 3: Illusion of Objectivity Read More »

Expert’s Curse 2: Intuition

Intuitive decision making, also known as naturalistic decision making (NDM), is often associated with experts. The scope of intuition ranges from the ultra-fast recollection of what was memorised before to simple gut feeling. It is essential, at this stage, to differentiate between intuition from heuristics (simple rules of thumb) and probabilistic estimation.

Firefighters and chess players are the favourite examples of the proponents of intuition. It is also a trait associated with people in creative fields. Grand master-level chess players can identify almost all the possible moves fast. Similarly, an experienced firefighter manoeuvres her actions effortlessly in times of crisis. A third example can be an F1 champion making an overtake and avoiding collision at 300 km/h speed! One thing common to all three experts is the number of hours they spend on practises. Let’s analyse these cases one by one.

A chess player or any other performing person, be in sports or arts, can not get help from a decision-making tool (e.g. a computer) during the act. So, irrespective of whether intuition is the best method or not, using the head remains the only option.

The firefighter does not have the time to perform a quantitative evaluation of each of the options she may have. Also, there is no guarantee that estimation is even possible in highly uncertain conditions. So they resort to recognising the patterns around them and applying the appropriate techniques from the hundreds they had encountered in their training and experience.

So intuition, that way, is restricted to those experts who have either no choice or no time. But for a doctor, a judge or a teacher, the situation is different. They have access to data, and support systems are available to collect and interpret more data. In such cases, more than their experience, the ability to avoid biases, acceptance of ignorance, and learner mindset are more valuable.

The final group include investment advisors, sports analysts and political commentators. They are experts who take pride in their experience and intuition. In reality, they work in fields filled with high levels of uncertainty, and, more often, their rates of success are no better than pure chances!

Daniel Kahneman and Gary Klein, “Conditions for intuitive expertise: a failure to disagree”, American Psychologist 64(6):515-26

Expert’s Curse 2: Intuition Read More »

Expert’s Curse 1: Base Rate Fallacy

The first one on the list is the base rate fallacy or base rate neglect. We have seen it before, and it is easier to understand the concept with the help of Bayes’ theorem.

P(H) in the above equation, the prior probability of my hypothesis on the event is the base rate. For the case study of doctors in the previous post, the problem starts when the patient presents a set of symptoms. Take the example of the case of UTI from the questionnaire:

Mr. Williams, a 65-year-old man, comes to the office for follow up of his osteoarthritis. He has noted foul-smelling urine and no pain or difficulty with urination. A urine dipstick shows trace blood. He has no particular preference for testing and wants your advice.

eAppendix 1.: Morgan DJ, Pineles L, Owczarzak, et al. Accuracy of Practitioner Estimates of Probability of Diagnosis Before and After Testing. Published online April 5, 2021. JAMA Internal Medicine. doi:10.1001/jamainternmed.2021.0269

The median estimate from the practitioners suggested that they guessed a one-in-four probability of UTI (ranging from 10% to 60%). In reality, based on historical data, such symptoms lead to less than one in a hundred!

Was it only the base rate?

I want to argue that the medical professionals made more than one error, i.e., base rate neglect. As evident from the answer to the last question, it could be a combination of two possible suspects—anchoring and the prosecutor’s fallacy. First, let’s look at the questions and answers.

A test to detect a disease for which prevalence is 1 out of 1000 has a sensitivity of 100% and specificity of 95%.

The median survey response was 95% post-test probability (in reality, 2%!) for a positive and 2% (in reality, 0) for a negative.

The prosecutor’s fallacy arises from the confusion between P(H|E) and P(E|H). In the present context, P(E|H), also called the sensitivity, was 100%, but the answers got anchored to 95% representing specificity. To understand what I just meant, look at the Bayes’ rule in a different form:

\\ \text{Chance of Disease after a +ve result} = \frac{Sensitivity * Prevalence}{Sensitivity * Prevalence + (1-Specificity)*(1- Prevalence)} \\ \\ \text{Chance of Disease after a -ve result} = \frac{(1- Sensitivity )* Prevalence}{(1- Sensitivity )* Prevalence + Specificity*(1 - Prevalence)}

So it is not a classical prosecutor’s case but more like getting hooked to 95%, irrespective of what it meant—it is more of a case of anchoring.

Expert’s Curse 1: Base Rate Fallacy Read More »

The Curse of Expertise 

Practitioners are experts. They could be medical practitioners, domain experts, lawyers and judges, leaders of organisations, sports persons-turned-pundits, to name a few. A lot of decision making rests on their shoulders, and the tool they often employ is experience. And experience is a double-edged sword! On the one hand, it makes them the most suitable people for the job, but on the other hand, they tend to ignore quantitative inference and rely on personal experience instead.

JAMA Internal Medicine collected responses from 723 practitioners from outpatient clinics in the US and published a paper in April 2021. The study aimed to estimate the understanding of risks and clinical decisions taken by medical practitioners. They included physicians and nurse practitioners. They were given a questionnaire to fill in the pretest and post-test probabilities of a set of illnesses. The requested post-test estimates included those after positive tests and negative tests.

The survey had five questions – four containing clinical scenarios (pneumonia, breast cancer, cardiac ischemia and UTI) and one hypothetical testing situation (a disease with 0.1% prevalence and test with 100% sensitivity and 95% specificity). The scientific evidence and the median responses are tabulated below:

Clinical
Scenario		Scientific
evidence 		Estimate
Resident
physician		Estimate
attending
physician		Estimate
Nurse
practitioner
Pneumonia
pretest
probability		25-42808580
post-test
after +ve test		46-65959595
post-test
after – ve test		10-19605050
breast cancer
pretest
probability		0.2 – 0.35210
post-test
after +ve test		3 – 9605060
post-test
after – ve test		< 0.055110
cardiac ischemia
pretest
probability		1-4.410515
post-test
after +ve test		2-11756090
post-test
after – ve test		0.43-2.55510
UTI
pretest
probability		0-1252030
post-test
after +ve test		0-8.377.59090
post-test
after – ve test		0-0.11555
Hypothetical
Scenario
post-test
after +ve test		2959595
post-test
after – ve test		0255

Those unheard are …

Before pointing fingers at the medical practitioners: you get this data because someone cared to measure, the specialists were happy to cooperate, and the Medical Association had the courage and insight to publish it. And the ultimate objective is quality improvement.

At the same time, the survey results suggest the lack of awareness of the element of probability in clinical practice and call for greater urgency to focus on scientific, evidence-based medical practice.

Morgan et al., JAMA Intern Med. 2021;181(6):747-755

The Curse of Expertise  Read More »

What the Eyewitness saw

We have seen earlier that much of the evidence, depending on the nature, gives only moderate separation of the probability distributions of guilty and innocent curves. Evidence from the eyewitness is a leader that plays a pivotal role in the trial process. The pioneering work of Elizabeth Loftus reveals a lot about the fallibility of memory and the malleability of the brain by misinformation.

It’s in the wording

The first one is on people’s ability to estimate. In one experiment, the participants were asked to guess about the height of a basketball player. One group was asked: “how tall was the player” and the other, “how short was”. The ‘tall’ group estimated a higher number on an average than the ‘short’; the height difference between the tall to short was about 15 mm!

In the second experiment, 100 students were shown a video involving motor accidents and asked a few questions in which 6 were test questions – three of them about what happened in the movie and three that did not. Half of the subjects were given questions that were framed using ‘a’, such as Did you see a …? The other half were asked using ‘the’, such as Did you see the …? An overwhelmingly more number of people responded yes to the ‘the’ questions than the ‘a’ queries, irrespective of whether those events happened in the movie or not.

The role of presupposition

It is about asking one question followed by a second one. The purpose of the first question is to plant some seeds in the participant to influence the subsequent one. Forty undergraduates at the University of Washington were shown a 3-min video taken from the film “diary of a student revolution”. In the end, they were given a questionnaire with 19 filler questions and one key question. Half of the people got the question: “was the leader of the four demonstrators a male?” and the other half “was the leader of the twelve demonstrators a male?”. A week later, the subjects were back to answer 12 questions in which one key question was “how many demonstrators did you see in the movie”. The people who were asked “12” gave an average of 8.85 as the answer, whereas the “4” gave 6.4.

And the result?

The results make descriptions by witnesses one of the least reliable forms of evidence to separate guilty from the innocent. Do you remember the d’ of 0.8 from the earlier post?

Loftus, E. F., Cognitive Psychology 7, 560-572

Elizabeth Loftus: Wiki

What the Eyewitness saw Read More »