The Ultimatum Game – The Game Theory Version
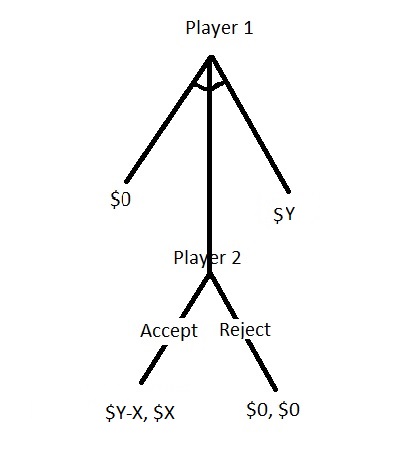
We have seen what behavioural scientists had observed when carrying out the ultimatum game on their subjects. Ultimatum game also has an economic side theorised by the game theorists for the rational decision-maker. A representation of the game is below.

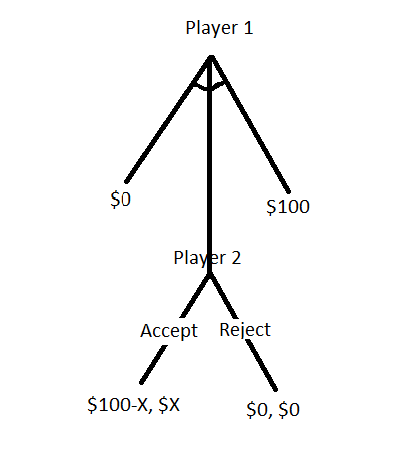
Unlike the simultaneous games we had seen before, where we used payoff matrices, this is a sequential game, i.e. the second person starts after the first one has made her move. The first type is a normal form game and is very static. The one shown in the tree above is an example of an extensive form game.
The game
Player A has ten dollars that she splits between her and player B. In the game design, A has to make the proposal and B can accept or reject it. If B accepts the offer, both the players get the money per the division proposed by A. If B refuses, no one gets anything.
Backward induction
Although player A starts the game by spitting 10 dollars between herself and player B, her decision gets influenced by what she assumes about B’s decision (accept/reject). In other words, A requires to begin from the ending and work backwards. Suppose player A does an unfair split 9-1 in favour of A. B can accept the 1 dollar or get nothing by rejecting. Since one is better than zero, B will probably take the offer. If A makes a fair split, then also B will accept the 5. That means B will take the offer no matter what A proposes. So player A may choose the unfair path. This is a Nash equilibrium.
What happens if player B makes a threat of rejecting the unfair offer. It may not be explicit; it could just be a feeling in A’s mind. In either case, player A believes in that and thus makes a fair division. And this is what Kahneman learned from his experiments. In-game theory language, the threat from B is known as an incredible threat as it makes no economic sense to refuse even the unfair offer (as 1 > 0)!
References
Games in the Normal Form: Nolan McCarty and Adam Meirowitz
Extensive Form Games: Nolan McCarty and Adam Meirowitz
The Ultimatum Game – The Game Theory Version Read More »