Decision Making

Chain Store Paradox – The Game

A chain store is challenged in town 1 by a rival. The store has two options – to go for a price war or acquiesce. In another town, town 2, another potential rival observes this and chooses to enter the market or quit. The chain store in Town 2 has to decide again whether to go for a price war or acquiesce with the new rival. Here are the payoffs:

The chain earns 0 when it goes to war
The chain earns 1 when it acquiesces
The chain earns 3 if the second rival quits
The second rival earns -1 from war
The second rival earns 0 from quitting
The second rival earns 1 from acquiesces

Note that rival 1 is already in town 1, and its payoff is irrelevant. Let’s draw the game tree and then solve the game using backward induction.

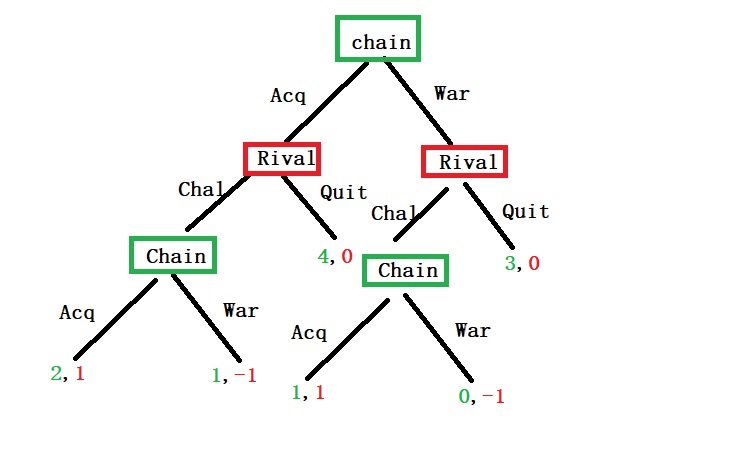
Step 1: payoffs at the lowest level

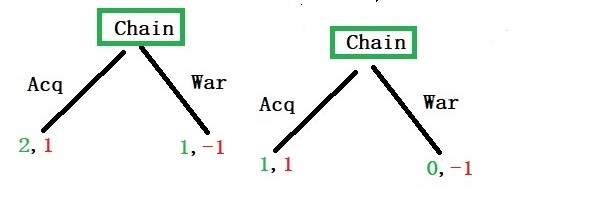
When the chain compares with the two options, acquiesce or war, it sees benefit for the former (2 > 1 and 1 > 0).

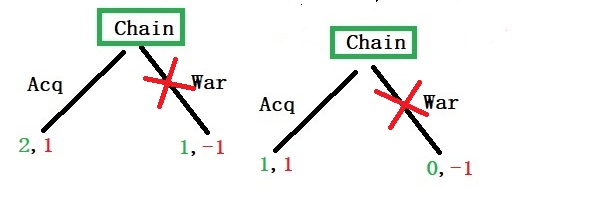
Step 2: One level up

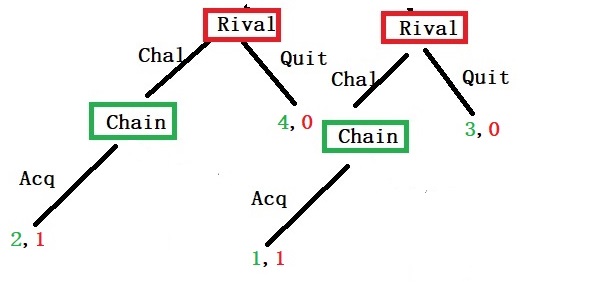
The rival knows (based on the backward induction logic) that the chain will choose to acquiesce over war. It can now decide to quit or challenge. Clearly, the benefit is in challenging (1 > 0 and 1 >0).

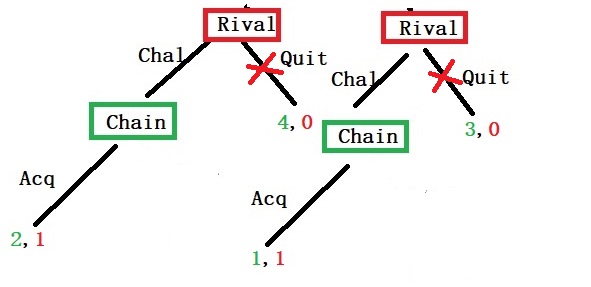
Step 3: Top level

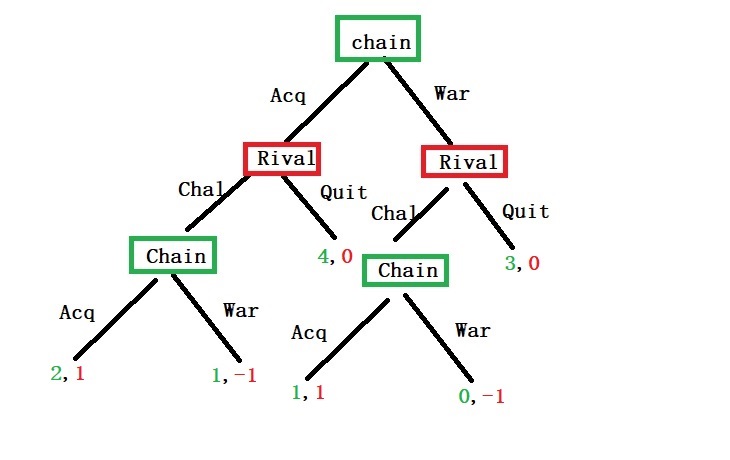
Extending the logic, one can expect the choice for the chain is to acquiesce over war. Therefore, in the following equilibrium, the chain store acquiesces, and the rival enters the market.

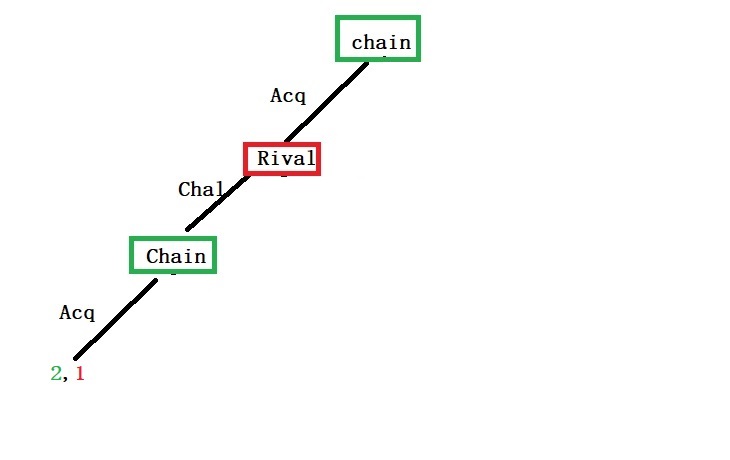
So, what is the paradox?

Chain Store Paradox – The Game Read More »

Cognitive Dissonance

What happens when a new idea or information contradicts your values or ideas? The mind feels the conflict and will resolve the issue by taking action until new ideas are consistent with the older ones. This lack of psychological agreement between two concepts is cognitive dissonance.

Consider an environmental activist who understands human-made. CO2 emissions and global warming when it comes to air travel. How will she react? She may do one or a mix of the following:
1) Reject air travel, at least where alternatives are available.
2) Change the belief in climate change that
2a) The whole theory is a scam
2b) Ignore as if nothing has happened
3) Get into a justification mindset that
3a) Others are also doing the same
3b) My travel is vital to justify a bit of emissions
3c) I did not cause the global warming in the first place

Cognitive dissonance: Wiki
Cognitive Dissonance: Sprouts

Cognitive Dissonance Read More »

Going for Three Pointer – Continued

Team A (Defend)
Defend 2Defend 3
Team B
(Shoot)		Shoot 2(0.18, 0.82)(0.31, 0.69)
Shoot 3(0.50, 0.50)(0.23, 0.77)

Let p be the probability for the shooting team to shoot a 3-pointer. The optimal value of p is such that the defending team get no incentive to defend a two over three.

The defensive team’s incentive to defend two = 0.82 (1-p) + 0.5 p
The defensive team’s incentive to defend three = 0.69 (1-p) + 0.77 p
Equating,
0.82 (1-p) + 0.5 p = 0.69 (1-p) + 0.77 p
0.82 p – 0.5 p – 0.69 p + 0.77 p = 0.82 – 0.69
p = 0.325

Let q be the probability for the defending team to defend a 3-pointer. At the optimal value of q, the shooting team get no incentive to shoot a two over three.

The shooting team’s incentive to shoot two = 0.18 (1-q) + 0.31 q
The shooting team’s incentive to shoot three = 0.5 (1-q) + 0.23 q
Equating,
0.18 (1-q) + 0.31 q = 0.5 (1-q) + 0.23 q
0.18 q – 0.31 q – 0.5 q + 0.23 p = 0.18 – 0.5
q = 0.8

Reference

Game theory applied to basketball by Shawn Ruminski: Mind Your Decisions.

Going for Three Pointer – Continued Read More »

Going for Three Pointer

Here is a game theory analysis of an end-of-game basketball scenario. This paper by Shawn Ruminski appeared in Presh Talwalkar’s blog, Mind Your Decisions. Here is the problem.

The fourth quarter is approaching its end. Team A is leading the game with two points and with the shot clock turned off. The ball is now with Team B. They have two choices: aim for a win with a three-point attempt or a tie (and Overtime) with a two-pointer attempt. What is the right strategy?

Here are some assumptions:

  1. Open 2-point Field Goal %: 62.5
  2. Open 3-point Field Goal %: 50.0
  3. Contested 2-point Field Goal %: 35.7
  4. Contested 3-point Field Goal %: 22.8
  5. The chance of winning the O/T is 50:50

Team B has two choices: attempt 2 or 3 points, and Team B has two: defend 2 or 3. Following are the payoffs.

If Team B goes for a 2-pointer and Team A defends against a 2-pointer. The probability of team B winning is 0.357 x 0.5 = 0.179 (FG% for a contested 2 pt followed by winning in O/T).

If Team B goes for a 2-pointer and Team A defends against a 3-pointer. The probability of team B winning is 0.625 x 0.5 = 0.313 (FG% for an open 2 pt followed by winning in O/T).

If Team B goes for a 3-pointer and Team A defends against a 2-pointer. The probability of team B winning is 0.5 x 1 = 0.5.

If Team B goes for a 3-pointer and Team A defends against a 3-pointer. The probability of team B winning is 0.228 x 1 = 0.228

Team A (Defend)
Defend 2Defend 3
Team B
(Shoot)		Shoot 2(0.18, 0.82)(0.31, 0.69)
Shoot 3(0.50, 0.50)(0.23, 0.77)

As you can see from the payoff matrix, there is no dominant strategy for either team; therefore, there must be a mixed strategy.

Reference

Game theory applied to basketball by Shawn Ruminski: Mind Your Decisions.

Going for Three Pointer Read More »

Properties of Risk

Howard Marks continues with his memos for his clients by explaining a few properties of risk. According to him:

Risk is counterintuitive

  1. The riskiest thing in the world is the belief that there is no risk. As per Nassim Taleb, the way many investors view the market is often worse than Russian Roulette. In Roulette, there is one bullet in one of the six chambers of the revolver. But in investing, the frequency of bad events is so scarce (many chambers) that people start believing that there is no bullet inside.
  2. Good awareness that the market is risky improves the investors’ due diligence, making it less risky.
  3. When the asset price declines, people think it becomes riskier to invest, but it actually becomes safer. The opposite is also true; when the price increases, people are attracted to it as a safe instrument, forgetting the asset has actually become riskier.
  4. Having only safe assets of one type (lack of diversification) can make the portfolio vulnerable. On the contrary, having a few riskier but different types can make the portfolio more diversified and less vulnerable.

Risk aversion makes markets safer

As seen above, a risk-conscious investor does proper due diligence on the market, makes conservative assumptions, and demands a higher premium for the risk.

Risk is invisible

Most of the knowledge of risk comes from hindsight, i.e., after the event has happened.

Risk control is not risk avoidance
While proper control is necessary, avoiding the risk altogether prevents the investor from reaching her goals.

Reference

Howard Mark’s Memo: Risk Revisited

Properties of Risk Read More »

The Capital Market Line: Illusion of Return

The relationship between risk and rewards, that reward increases with risk, is much engrossed in common knowledge. In investing, we have seen portfolio theory and capital market lines that confirm this notion.

But the risk-return line is far from straight. We have seen earlier that the X-axis (risk) in the case of an investment is the volatility of the portfolio. In the language of statistics, volatility is the standard deviation of the distribution. In other words, each point of the line represents a distribution (of returns), with higher and higher standard deviations from left to right.

While the expected returns, the mean of the distribution, are higher to the right, the chances of higher and lower returns (including losses) are also higher. The critical issue here is that no one knows the breadth of the distribution or its shape. Imagine if it is what Nassim Taleb calls a fat tail, an asymmetric distribution, or the occurrence of a heavy impact-low probability event.

Reference

Howard Mark’s Memo on Risk

The Capital Market Line: Illusion of Return Read More »

Risk and Return – The Capital Market Line

We have seen how simple portfolio theory explains the relationship between risk and returns. For example, the representation below.

This leads to the development of what is known as the Capital Market Line (CML). CML is a concept that combines the risk-free asset and the market portfolio. It is the line connecting the risk-free return and tangent to the ‘efficient frontier’ of the portfolio.

The slope of the Capital Market Line (CML) is the Sharpe Ratio of the portfolio.
Sharpe Ratio = (Return of the portfolio – risk-free rate) / Standard deviation

But there is something wrong with this line – or at least how people perceive the line of risk vs return. That is, next.

Risk and Return – The Capital Market Line Read More »

Duel – Backward Induction

In the previous post, we developed the condition for the player to shoot the opponent. I.e., the distance (d*) at which the probability of the player who gets the turn is greater than or equal to the chance of the opposite missing in the next turn.

When the player, say P1, reaches d*, she can believe in two things. 1) P2 will not shoot in the next turn (d*-1) or
2) P2 will shoot in the next turn.
In the first case, P1 should not shoot. In the second case, P1 assesses that P1(d*) + P2(d*-1) = 1. So, P1 must shoot.

But what should Player 1 believe? The answer comes from backward induction.

Imagine the players came in close range (d = 0), and it’s P2’s turn. P2 will shoot and win. Taken one step back: P1 knows that in the next step, P2 will shoot, so she takes option 2. She assesses that P1(1) + P2(0) > 1, and she shoots. Go back one more step. Now, P2 knows that P1 will shoot in the next step, and if the distance is less than d*, P2 must shoot. It will continue until d* is reached.

Duel – Backward Induction Read More »

Duel

There are two players in the duel game, P1 and P2. Each carries a pistol loaded with a single bullet positioned a certain distance apart. Each player gets one round at a time, one after another. A player can shoot the other or step forward in her turn. Whoever hits the other wins the game. So, the player’s strategic decision is when she should shoot.

Let Pi(d) be the probability that player i will get her target (the opponent) from a distance d. The two players can have different abilities. In other words, P1(d) can be lower (or higher) than P2(d). Also, at d = 0, P1 and P2 hit the target (P1(0) = P2(0) = 1).

So, who will take the shot first, and when?

Imagine it’s P1’s turn, and she can believe in the following two things:
1) P2 will not shoot in the next turn
2) P2 will shoot in the next turn

If P1 believes in option 1 (that P2 will not shoot in the next turn), P1 will not shoot in this turn. If P1 thinks that P2 will shoot, then P1 will evaluate her options in the following manner. If P1 thinks her probability of hitting the target in this turn is greater than or equal to her opponent’s chance to miss in the next turn, she will shoot. Mathematically, that is:

P1(d) >/= 1 – P2(d-1) or
P1(d) + P2(d-1) >/= 1

The distance at which the condition is satisfied is d*. From the picture, it is clear that below d*, the probability, P1(d) + P2(d-1) > 1 and above d*, it is < 1.

Duel Read More »

Only Trade-Offs

American economist and political commentator Thomas Sowell summarises the core of decision-making, like nobody has, in his famous quote: There Are No Solutions, Only Trade-offs.

A crucial thing in trade-off is the assessment of the consequence of each option. A common practice in investment decisions is the cost-benefit analysis.

Only Trade-Offs Read More »