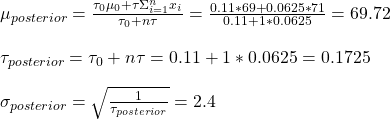Data & Statistics

The Framing of the Risk in Decision Making

We have seen three questions and the public response to those in the last post. While the expected value theory provides a decent conceptual basis, real-life decisions are typically taken based on risk perception, sometimes collected in the utility functions. Let’s analyse options and the popular answers to the three questions.

80% preference for sure $30 vs 80% chance for $45 is a clear case of risk aversion in all forms. People were willing to ignore that 8 out of 10 would get $45 had they given up the $30 in the bank.

Understanding the response to the second question was easy. The first stage was mandatory for the participants to play, and the options in the second stage were identical to the first question.

The intriguing response was the third one. In reality, the second and third questions are the same. Yet, almost half of people who went for the sure-shot $30 are now willing to bet for $45!

Tversky, A.; Kahneman, D., Science, 1981, 211, 453

The Framing of the Risk in Decision Making Read More »

Utility Model in practice

We have seen how a rational decision-maker may operate using either the expected value or the expected utility theory. Real-life, however, is not so straightforward about these kinds of outcomes. In a famous Tversky-Kahneman experiment, three groups were presented with three situations.

1: Which of the following do you prefer?
A. a sure win of $30
B. 80% chance to win $45

2: There is a two-stage game with a 25% chance to advance to the second stage. After reaching the second, you get the following choices, but you must give the preference before the first stage. If you fail in the first, you get nothing.
C. a sure win of $30
D. 80% chance to win $45

3: Which of the following do you prefer?
E. 25% chance to win $30
F. 20% chance to win $45

Expected Values

We will look at the expected values of each of the options. You will argue that it’s not how people make decisions in real-life. But, keep it as a reference. Remember: EV = value x chance, summed over.

CaseEV
A$30
B$36 ($45 x 0.8)
C$7.5 (0.25 x $30)
D$9 (0.25 x $45 x 0.8)
E$7.5 (0.25 x $30)
F$9 (0.2 x $45)
I have highlighted the higher EVs (of the choices) in bold.

What did people say?

In the first group, 78% of the participants chose option A. In the second, it was 74% in favour of option C. It was almost a tie (42% for E and 58% for F) for the final group.

These three problems are, in one way, similar to each other. We will see that next.

Tversky, A.; Kahneman, D., Science, 1981, 211, 453

Utility Model in practice Read More »

Framing the Risk

We are back with Tversky and Kahneman. This time, it is about decision making based on how the risk appears to you. There is one problem statement with two choices. Two groups of participants were selected and given this but in two different formats.

Here is the question in the first format: imagine that the country is bracing for a disease that can kill 600 people. Two programs have been proposed to deal with the illness – program 1 can save 200 people, and program 2 gives 1/3 probability to save all and 2/3 chance to save none. Which of the two do you prefer? 72% of the people chose program 1.

The second group of participants was given the same problem with different framing. Program 3 will lead to 400 people dying, and program 4 has a 1/3 probability that none will die and 2/3 probability that all will die. 78% of the respondents chose program 4!

Risk aversion and risk taking

Identical problems, but the choices are the opposite! The first case sounded like saving lives, and the players chose what appears to be a risk-averse solution. In the second case, the options sounded like losing lives, and people were willing to take the risk and went for the probabilistic solution.

Tversky, A.; Kahneman, D., Science, 1981, 211, 453

Framing the Risk Read More »

The Myth of Benevolent Dictator

The gulf between what we all like to believe and what happens can be wide. We have seen this before in the one-child policy of China. We called it the claim instinct. Because it contained the perfect recipe – a mighty leader, an intervention and results that fitted a narrative.

We look at a similar one today – that of benevolent dictator. The phrase may sound like an oxymoron for anybody who lives in the modern world. The benevolent autocrat is a school of thought on leadership, and its proponents take examples from countries such as Singapore as their test case. As per this school, these well-intended rulers bring higher economic prosperity to their countries.

The paper written by Rizio and Skali examined this claim by collecting data from 133 countries over 150 years starting from 1858. Their mathematical analysis consisted of three variables – rulers (taken from Archigos database), political regime (Polity IV dataset), and GDP per capita (Maddison dataset).

Misguided belief in dictators

The results showed that good dictators brought prosperity no different from what chance would have made. At the same time, bad dictatorships showed a clear negative impact on the economy.

References

S.M. Rizio and A. Skali, The Leadership Quarterly 31 (2020) 101302
Introducing Archigos: A Dataset of Political Leaders
Polity IV Individual Country Regime Trends
Maddison Project Database 2013

The Myth of Benevolent Dictator Read More »

Top Risks Lead to Top Priorities

What should be our top priority in life? Well, it depends on the top risks in life. Depending on whom you ask this question, the answer may vary.

Top priorities

I suspect risk to life comes first. What else can come closer or even be ranked higher? To a large section of the world, it could simply be getting out of poverty. It can be so powerful that individuals may even risk their lives to achieve it for their families and future generations at least. Here, I assume that, at least for the people who read this post, the risk to life is the top one.

Top risks to life

What is the top risk to life? It could be diseases, accidents, extreme weather events, wars, terrorist attacks, etc. Let’s explore this further. According to the World Health Organization (WHO), diseases are the top 10 causes of death and are responsible for 32 out of the 56 million deaths in a year. That is about 60%, according to the 2019 data. And what are they?

Noncommunicable diseases occupied the top seven spots in 2019. Yes, that will change in 2020 and 21, thanks to the COVID-19 pandemic. Deaths due to the current pandemic can reach the top three in 2021, but getting into the top spot is unlikely, at least based on the official records.

The Oscar goes to

The unrivalled winner is cardiovascular diseases (CVDs) – heart attacks and strokes – which cost 18 mln lives in 2019. The risk factors include unhealthy diets, physical inactivity, smoking, and the harmful use of alcohol. And an early warning to watch out for is high blood pressure.

There are three ways to manage the top risk: 1) medication for blood pressure management, 2) regular exercise, and 3) getting into the habit of a healthy diet.

Top 10 causes of death: WHO

Cardiovascular diseases: WHO

Top Risks Lead to Top Priorities Read More »

Anscombe’s Trap

What is so special about the following four scatter plots? Do you see any similarities between them?

Well, all four look different from each other. The first is a scatter plot with a linear trend, the second is a curve, the third represents a straight line with one outlier, and the fourth is a collection of points in a cluster with an extreme outlier. And you are right; they represent four different behaviours or x and y.

Beware of statistical summary

Imagine you don’t get to see how they are organised in the x-y plane, but instead, only the summary statistics, and here they are:

PropertyValue
Mean x 9.0
Mean y 7.5
Sample variance of x11
Sample variance of x4.12
Correlation between x and y0.816
By the way, the numbers above represent all four sets!

Not over yet!

Now put linear regression lines to all.

And if you don’t believe me, see all four in one plot with the common linear regression line.

Following is the complete dataset in an R data frame.

Q1 <- data.frame("x" = c(10, 8, 13, 9.0, 11.0, 14.0, 6.0, 4.0, 12.0, 7.0, 5.0), "y" = c(8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68))
Q2 <- data.frame("x" = c(10, 8, 13, 9.0, 11.0, 14.0, 6.0, 4.0, 12.0, 7.0, 5.0), "y" = c(9.14, 8.14, 8.74, 8.77, 9.26, 8.10, 6.13, 3.10, 9.13, 7.26, 4.74))
Q3 <- data.frame("x" = c(10, 8, 13, 9.0, 11.0, 14.0, 6.0, 4.0, 12.0, 7.0, 5.0), "y" = c(7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73))
Q4 <- data.frame("x" = c(8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8), "y" = c(6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.50, 5.56, 7.91, 6.89))

The moral of the story is

Summary statistics are great ways to communicate trends. But, as the reviewer, you must exercise the utmost care in understanding the actual data points.

Anscombe’s quartet: wiki

Anscombe’s Trap Read More »

Normal – Normal Sensitivity

In this fourth and final episode on the Bayesian inference with normal-normal conjugate pair, we find out how important is the choice for the prior and data collection in arriving at the answer. We will start from the previous set of inputs. But the relationship between the prior and the posterior first.

\\ \mu_{posterior} = \frac{\tau_0 \mu_0 + \tau \Sigma_{i=1}^{n} x_i}{\tau_0 + n*\tau} \\ \tau_{posterior} = \tau_0 + n*\tau \\ \sigma_{posterior} = \sqrt{\frac{1}{\tau_{posterior} }}

The parameters used in the first example are:

\\ \mu = \text {variable}; \sigma = 2 \text { (hypothesis)} \\ \mu_0 = 15; \sigma_0 = 4 \text { (prior)} \\ x = 9 \text{ (data)}

And the output is plotted below. The green curve is the prior probability distribution, blue represents the posterior in case of one data and red for 5 data (same value of 9). The vertical dotted line points at the data (or the average of the data).

It shows that (multiple) data at nine is pulling the distribution to come closer to it. Now let’s change the prior further right, mu0 = 25.

You see that the posterior distributions did not change much. Next, we will make the distribution narrower by defining sigma0 to be 2 and keeping mu0 at 25.

Things are now beginning to separate from the data. This suggests that if you want to be conservative with the estimation of posterior, it is better to keep the prior distribution narrower.

Finally, we check the impact of the standard deviation of the hypothesis. We change the value from 2 to 4, while keeping the original parameters as they are (mu_0 = 15; sigma_0 = 4):

Compare this with the first plot: you will see that making the hypothesis broader did not impact the mean value of the posterior.

Previous Posts on Normal-Normal

Normal-Normal conjugate
Normal-Normal and height distribution
Normal-Normal continued

Normal – Normal Sensitivity Read More »

Normal – Normal Continued

We will do a few sensitivities and see how the posterior distribution modifies. Let’s define the variables before we start.

\\ \mu = \text {variable}; \sigma = 2 \text { (hypothesis)} \\ \\ \mu_0 = 15; \sigma_0 = 4 \text { (prior)} \\ \\ x = 9 \text{ (data)}

The plots of the distributions are

Imagine you collected four more data, and interestingly they are all the same, 9! You have five data points now, although the average remains the same (9) as the previous case.

Note that the vertical dotted line represents the data (or the average of the data).

The relations used in the calculations of the posteriors are:

\\ \mu_{posterior} = \frac{\tau_0 \mu_0 + \tau \Sigma_{i=1}^{n} x_i}{\tau_0 + n\tau} \\ \\ \tau_{posterior} = \tau_0 + n\tau \\ \\ \sigma_{posterior} = \sqrt{\frac{1}{\tau_{posterior} }}

Normal – Normal Continued Read More »

Normal – Normal and Height Distribution

Continuing from the previous post, we will apply the normal-normal Bayesian inference to the height problem. The general format of the Bayes’ rule is:

P(\text{height distribution}|height = 71)= \frac{Likelihood (height = 71|\text{a height distribution}) * P(\text{height distribution})}{\int Likelihood (height = 71|\text{a height distribution}) * P(\text{height distribution})}

Since there are two parameters involved in the normal distribution, we have to have either a double integral in the denominator or choose one of the parameters, say the standard deviations, as known. So, we assume the standard deviation to be 4.0 in the present case. Let’s take the mean for the prior to be 69, the standard deviation to be 3 and see what happens. Therefore,

\\ \mu = variable, unknown \\ \sigma = 4 \\ \tau = \frac{1}{\sigma^2} = 0.0625 \\ \mu_0 = 69 \\ \sigma_0 = 3 \\ \tau_0 = \frac{1}{\sigma_0^2} = 0.11 \\ \text{You will soon find out why I have defined }\tau

Now we have everything to complete the problem.

\\ \mu_{posterior} = \frac{\tau_0 \mu_0 + \tau \Sigma_{i=1}^{n} x_i}{\tau_0 + n\tau} = \frac{0.11 * 69 + 0.0625*71}{0.11 + 1*0.0625} = 69.72 \\ \\ \tau_{posterior} = \tau_0 + n\tau = 0.11 + 1*0.0625 = 0.1725 \\ \\ \sigma_{posterior} = \sqrt{\frac{1}{\tau_{posterior} }} = 2.4

You can see a few things here: 1) the prior has moved a bit in the direction of the data but is still far from it, 2) the posterior is narrower than the prior.

Normal – Normal and Height Distribution Read More »

Normal – Normal Conjugate

We have seen how to come up with estimates of events based on assumed prior data using Bayesian inference. For discrete events that are rare, we have Poisson likelihood, and on such occasions, we use a Gamma prior and get a gamma posterior. In the same manner for Shaq, we found that the best one for estimating his success (or the lack of it) of entering Whitehouse is a binomial distribution. Once a data point is collected (one attempt), you update the chances using a beta distribution as a prior, and you get beta as the posterior.

Here is a new challenge you have a task to estimate the male height distribution of a particular country. We know from the examples of other countries that normal distributions describe the height distributions. A normal distribution has two parameters – mean and standard deviation, and our challenge is to estimate these parameters for our new country. We start with a set of hypotheses, use the available data and apply Bayesian inference to reach the goal.

Assume that I have collected data from the region, and it is 71 inches. Now I assume that the means ranges from 50 to 80 inches and the standard deviation from 1 to 4. Collect five hypotheses (purely random) from them as follows:

N(mean = 60, sd = 2), N(71, 3), N(65, 1.5), N(75, 4), N (80,1)

Now ask the question: what is the likelihood that my distribution of the new country is N(75, 4) given that I have collected data of 71 inches? Same for the rest four of the hypotheses. It can be estimated utilising the standard tables or using the R function dnorm(71, 75,4) = 0.06049268. The Pictorial representation is below.

Before applying the Bayes’ theory, we should realise that 1) we need prior probabilities for each of the above five hypotheses and 2) we can have infinite hypotheses, not just five! Then we can apply the formula as we did before.

\\ P(\text{height distribution}|height = 71)= \frac{Likelihood (height = 71|\text{a height distribution}) * P(\text{height distribution})}{\int Likelihood (height = 71|\text{a height distribution}) * P(\text{height distribution})}

It is a conjugate problem (the prior will be a pdf), and the right prior is a normal distribution, making it a normal-normal problem. How to complete the exercise using normal-normal is something we will see next.

Normal – Normal Conjugate Read More »