The Myside Bias
The last few posts covered one important aspect of our irrationality. That it is beyond the education level or other types of cognitive deficiencies, but purely ideological. The author Steven Pinker calls it the myside bias.
The last few posts covered one important aspect of our irrationality. That it is beyond the education level or other types of cognitive deficiencies, but purely ideological. The author Steven Pinker calls it the myside bias.
The irrationality of the public on subjects of global impacts, such as climate change, has been explained using three dominant theories. They are 1) the scientific illiteracy theory, 2) the bounded rationality theory, and 3) the cultural cognition theory. The first assumes that most people lack the science education to understand the complex nature of global warming. The second one goes hand in hand with Kahneman’s definition of system 1 (fast) and system 2 (slow) thinking. The third one concerns the perception of risks and how they fit with an individual’s value systems.
To apply this to climate change: a familiar narrative is that the average public lacks the capacity to comprehend the science behind it and therefore resorts to some form of heuristics to understand, which is often governed by her beliefs. The name associated with this portrayal is the public irrationality thesis (PIT).
Kahan et al. have applied the theory to testing. Contrary to the expectation, in his first test (N = 1540), he found that increased science literacy and numeracy did not increase the risk perception of climate change; in fact, it slightly decreased!
On the other hand, the study found that an egalitarian individual (communitarian) is more likely to have a higher risk perception of climate than a hierarchical person (individualist). It remained the same or slightly increased with her numeracy. It was striking that the hierarchical individualist did not progress her risk perception as a function of numeracy; instead, it slightly reduced!
On the other hand, to answer the question about the impact of nuclear power on human health and safety, both types of individuals showed reduced perceived risks as a function of their literacy.
Both these data suggest that increasing science education and numeracy is not necessarily to help detach oneself from her beliefs.
Motivated Reasoning – Climate Change Read More »
We have seen how different distributions converge to Gaussian, which is one fundamental property of statistics known as the central limit theorem (CLT). The second all-important property is the Law of Large Numbers (LNN). The following three plots show how that happens.
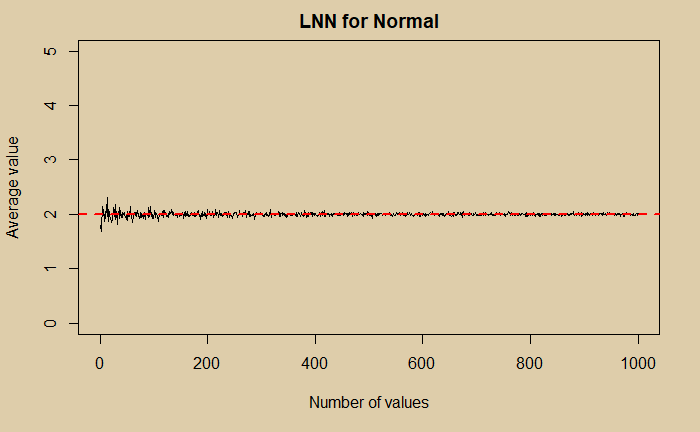
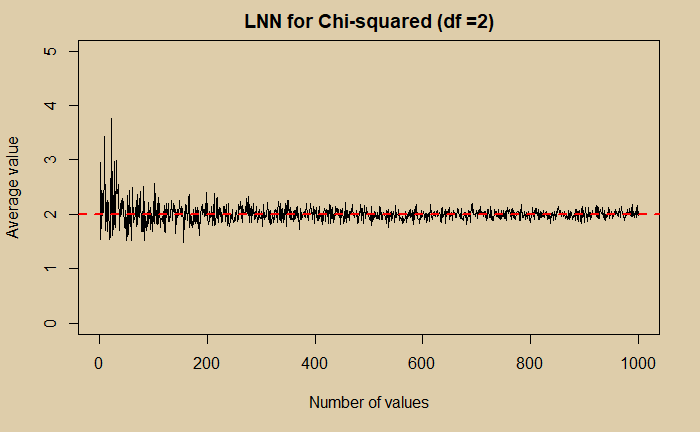
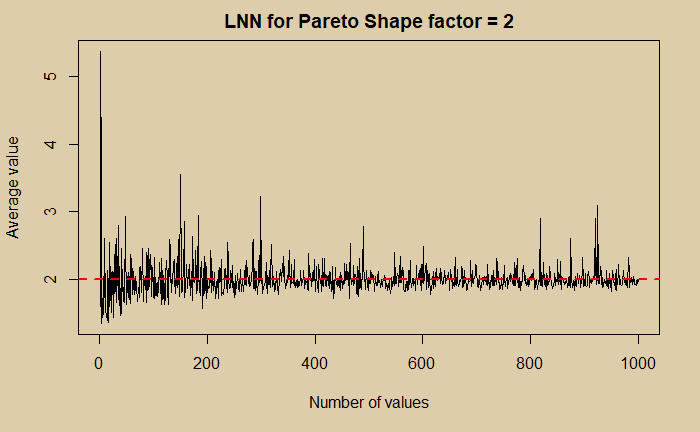
LNN for Pareto Distribution Read More »
We have seen how samples from almost any distribution, provided you collected enough for the average, eventually make Gaussian, which is the Central Limit Theorem (CLT). We also see the futility of that assumption when dealing with asymmetric distributions such as the Pareto; ‘enough for the average‘ never happens with any practical numbers of sampling.
Once we assume that all samples obey CLT (which is already not a correct assumption), we start collecting data and finding out relationships. One of the pitfalls many researchers fall into is inadequate quality assurance and mistaking randomness as correlations. Here is an example. Following are six plots obtained by running two sets of standard normal distributions for random numbers (20 each) and plotting them on each other.
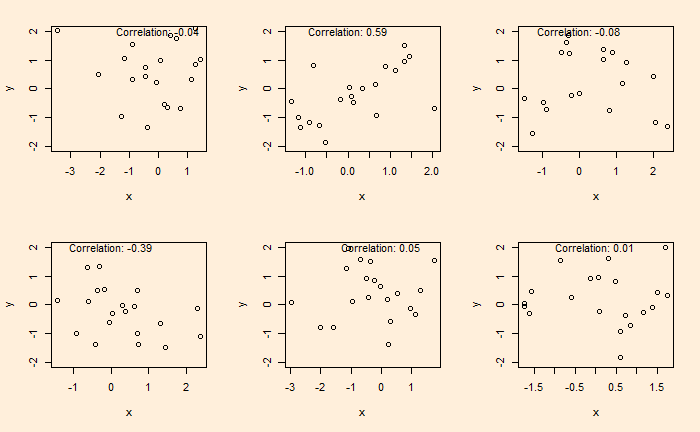
The plots are generated by running the following codes a few times.
x <- rnorm(20)
y <- rnorm(20)
plot(x,y, ylim = c(-2,2))
text(paste("Correlation:", round(cor(x, y), 2)), x = 0, y = 2)A nice video on this topic by Nassim Taleb is in the reference. Note that I do not support his views on sociologists and psychologists, but I do acknowledge the fact that a lot of results generated by investigators are dubious.
Fooled by Metrics: Taleb
Illusion of Correlation Read More »
Pareto is an asymmetric distribution; useful in describing practical applications such as uncertainties in business and economics. An example is the 80:20 rule, which suggests that 80% of the outcome (wealth) is caused (controlled) by 20%. It’s a special case of Pareto distribution with a shape factor = 1.16.
Let’s see how they appear for shape factor = 2.
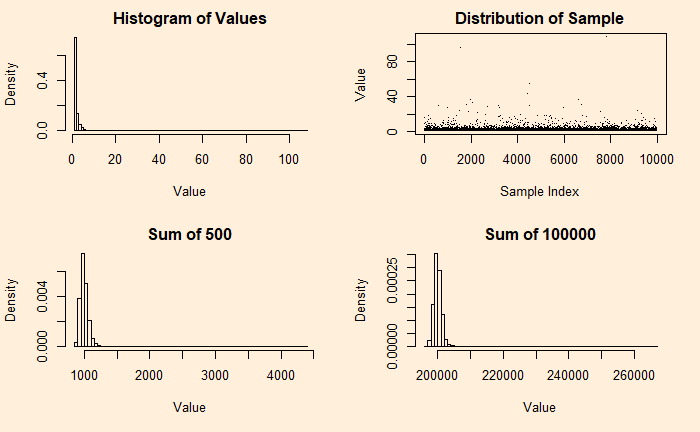
Even after 100,000 additions, the distribution has not become a Gaussian. Recall that a coin with a 95% bias is close to a bell curve after 500 additions.
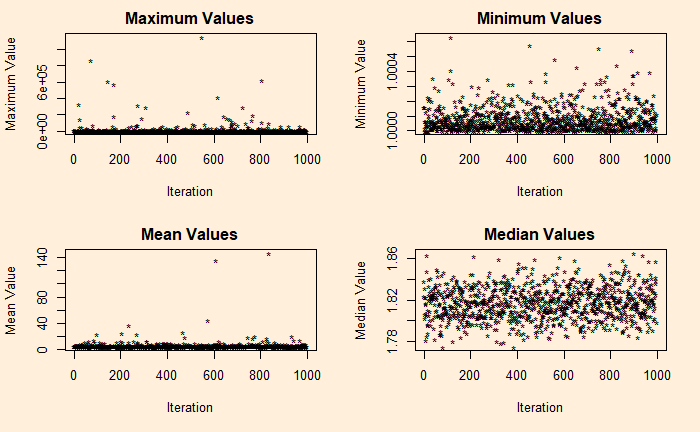
If you want to understand the asymmetry of Pareto, see the following four plots describing the maximum, minimum, mean and median of 10,000 samples collected from the distribution, repeated about 1000 times (Monte Carlo) for the plot.
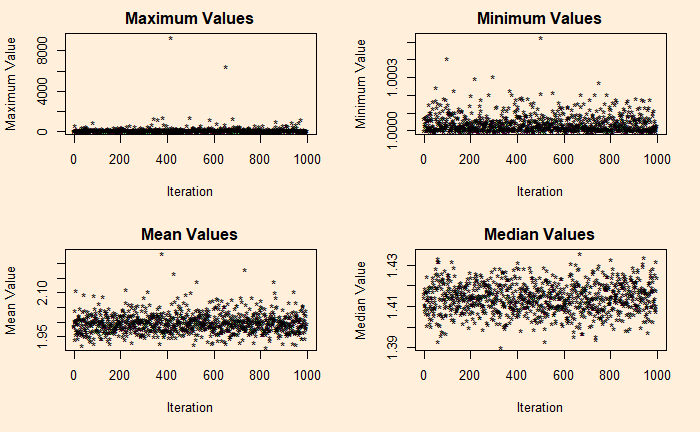
It’s a total terror for shape factor = 1.16 (the 80:20) – a median of 1.8 and a maximum close to a million!
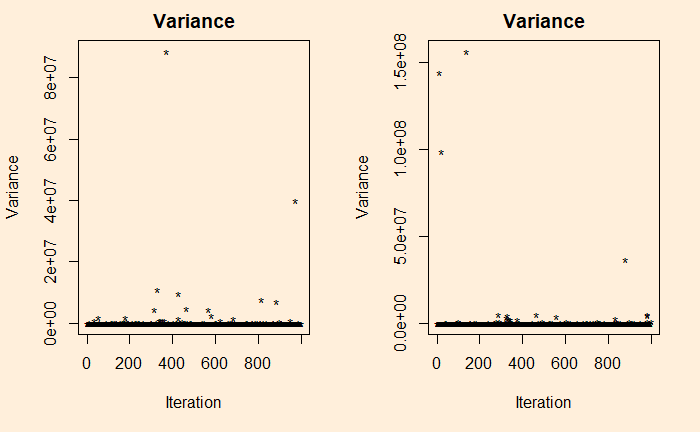
Want to see the variance?
Pareto distribution: Wiki
The 80-20 Rule: Investopedia
The Central Limit Theorem – Pareto Read More »
We have seen a demonstration of CLT using uniform distribution as the underlying scheme. But a uniform distribution is symmetric, so what about nonsymmetric?
It is more intuitive, to begin with, discrete before getting into continuous. So, let’s build the case from a simple experiment set – the tossing of coins. We start with the fair coin, toss it 10000 times and collect the distribution.
par(bg = "antiquewhite1", mfrow = c(1,2))
h1 <- sample(c(1,2), 10000, replace = TRUE, prob = c(0.5,0.5))
hist(h1, freq = TRUE, main = "Distribution - Coin Toss", xlab = "Outcome", ylab = "Frequency")
plot(h1, pch = "*", main = "Outcomes - Coin Toss", xlab = "Toss #", ylab = "Outcome" )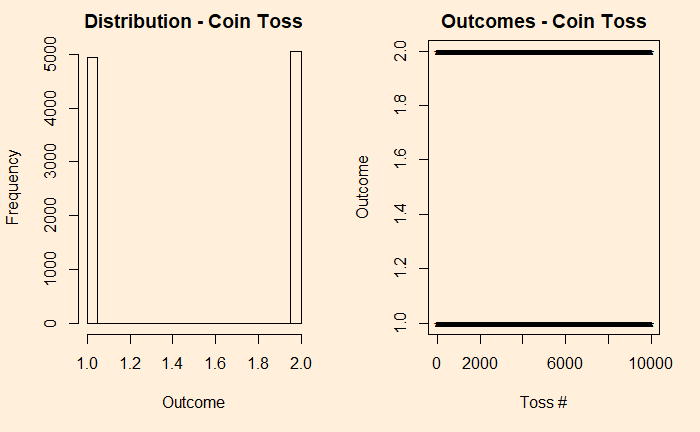
We denote the outcomes 1 for heads and 2 for tails. In the plot on the right-hand side, you see those 10,000 points distributed between the two. Now, introduce a bias to the coin – 95% heads (1) and 5% tails (2) and reduce the experiments to 1000 for better visualisation of the low probability state.
h11 <- sample(c(1,2), 1000, replace = TRUE, prob = c(0.95,0.05))
hist(h11, freq = TRUE, main = "Distribution - Coin Toss", xlab = "Outcome", ylab = "Frequency")
plot(h11, pch = "*", main = "Outcomes - Coin Toss", xlab = "Toss #", ylab = "Outcome" )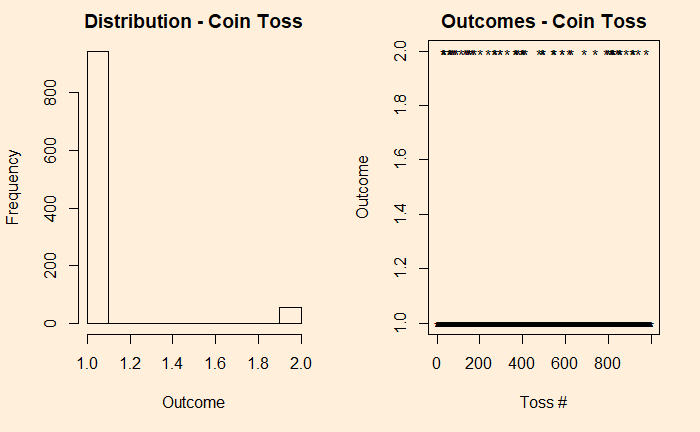
Now, add each distribution 25 times and check what happens.
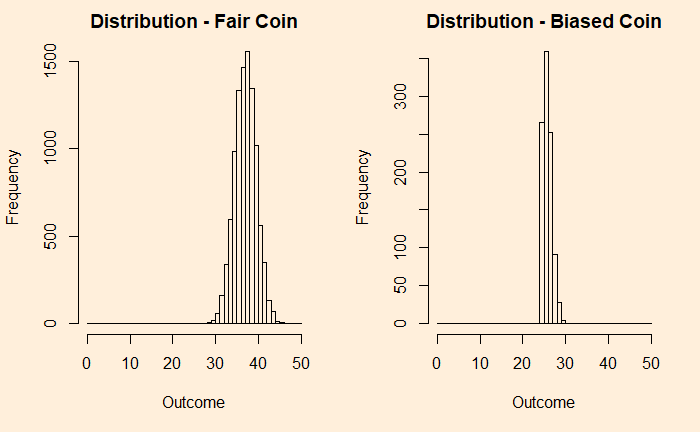
You can see that the fair coin has already started converging to a Gaussian, whereas the biased one has a long way to go. We repeat the exercise for 500 additions before we get a decent fit to a normal distribution (below).
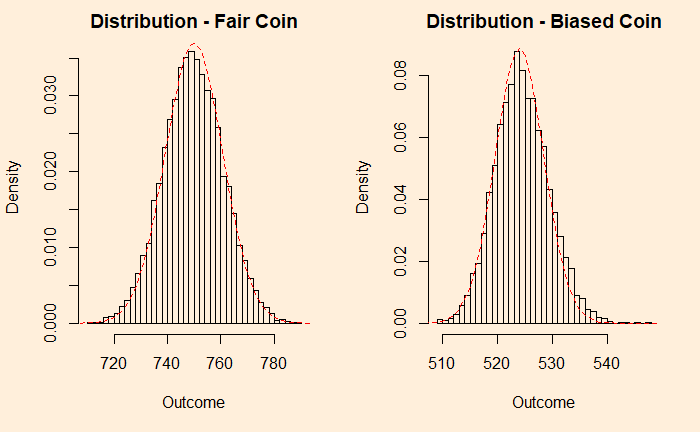
You can still see a bit of a tail protruding outside the reference line. So it didn’t matter what distribution you started with; as long as you got an adequate number of samples, the sums are normally distributed.
An example from the continuous family is the chi2 distribution with the degrees of freedom (df) 2. Following are two plots – the one on the left is the original chi2, and the right is adding 50 such distributions.
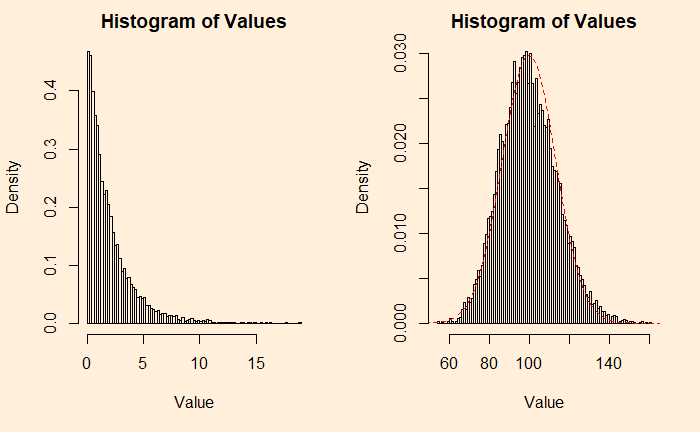
plots <- 1
plot_holder <- replicate(1,0)
for (i in 1:plots){
add_plot1 <- plot_holder + rchisq(10000, df=2)
plot_holder <- add_plot1
}
par(bg = "antiquewhite1", mfrow = c(1,2))
hist(add_plot1, breaks = 100, main = 'Histogram of Values', xlab = "Value", ylab = "Density", freq = FALSE)
plots <- 50
plot_holder <- replicate(1,0)
for (i in 1:plots){
add_plot2 <- plot_holder + rchisq(10000, df=2)
plot_holder <- add_plot2
}
hist(add_plot2, breaks = 100, main = 'Histogram of Values', xlab = "Value", ylab = "Density", freq = FALSE)
lines(seq(0,200), dnorm(seq(0,200), mean = 99.8, sd = 13.4), col = "red",lty= 2)Although we have used additions (of samples) to prove the point, the averages, which are of more practical importance, will behave the same way; after all, averages are nothing but additions divided by a constant (total number of samples).
The Central Limit Theorem for Non-Symmetric Read More »
Today, we will redo something we did cover in an earlier post – the sum of distributions. It directly demonstrates what we know as the central limit theorem (CLT). We will use R codes for this purpose.
We start with a uniform distribution. But what is that? As its name suggests, it is a class of continuous distribution and can take any value between the bounds with equal probabilities. Or the values are uniformly distributed between the boundaries.
There are many real-life examples of uniform distribution but of the discrete type, e.g., coin toss, dice rolling, and drawing cards. The resting direction of a spinner, perhaps, is an example of a continuous uniform.

As an illustration, see what happens if I collect 1000 observations from a uniform distribution set between 0 and 2.
uni_dist <- runif(n = 10000, min = 0, max = 2) # or simply, runif(10000,0,2)
plot(uni_dist, main = 'Distribution of Sample', xlab = "Sample Index", ylab = "Value", breaks = 100)
Look closely; can you see patterns in the plot? Well, that is just an illusion caused by randomness. Historically, such observations confused the public. The famous one is the story of flying bombs in the Second World War.
Some people like a different representation of the same plot – the histogram. A histogram provides each value and its contributions (frequencies, densities, etc.).
uni_dist <- runif(n = 10000, min = 0, max = 2)
hist(uni_dist, main = 'Histogram of Values', xlab = "Value", ylab = "Frequency", breaks = 100)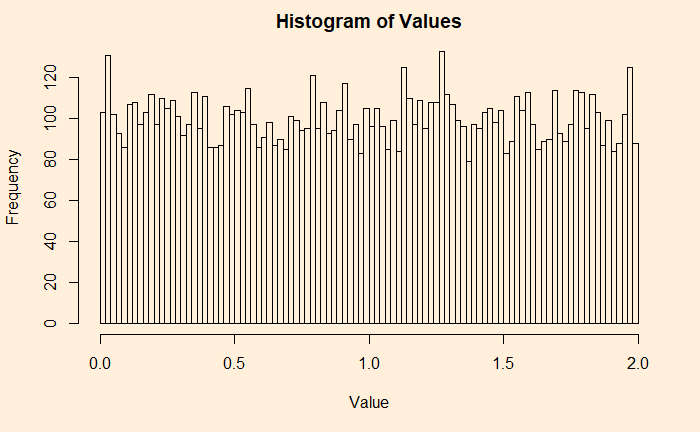
Now, you will appreciate why it is a uniform distribution. I have 100 bins (or bars), and each carries more or less 100 (frequency) values, making it 100000 overall.
If you don’t like frequencies on the Y-axis, switch it off, and you get densities.
hist(uni_dist, main = 'Histogram of Values', xlab = "Value", ylab = "Density", breaks = 100, freq = FALSE)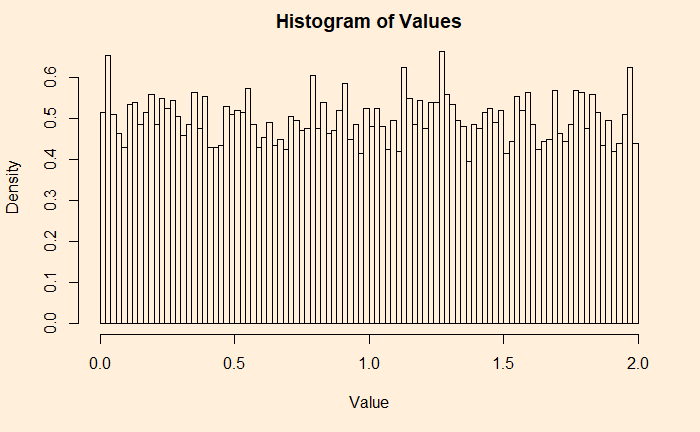
Adding two such independent sample data is the start of the CLT.
uni_dist1 <- runif(n = 10000, min = 0, max = 2)
uni_dist2 <- runif(n = 10000, min = 0, max = 2)
hist(uni_dist1+uni_dist2, main = 'Histogram of Values', xlab = "Value", ylab = "Frequency", breaks = 100)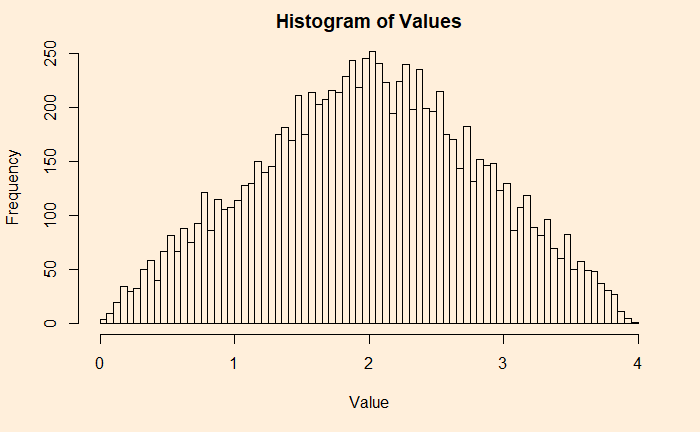
Let’s make a code and automate the addition by placing the calculation into a loop.
plots <- 25
plot_holder <- replicate(1,0)
for (i in 1:plots){
add_plot <- plot_holder + runif(10000,0,2)
plot_holder <- add_plot
}
his_ar <- hist(plot_holder, xlim = c(0, 2*plots), breaks = 2*plots, main = 'Histogram of Values', xlab = "Value", ylab = "Frequency", freq = FALSE)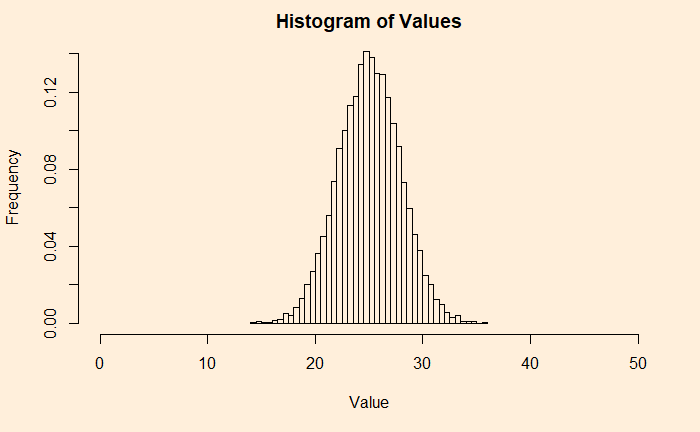
Here is a Gaussian, and hence the CLT. Verify it by adding a line from a uniform distribution and match.
lines(seq(0,2*plots), dnorm(seq(0,2*plots), mean = plots, sd = 2.8), col = "red",lty= 2)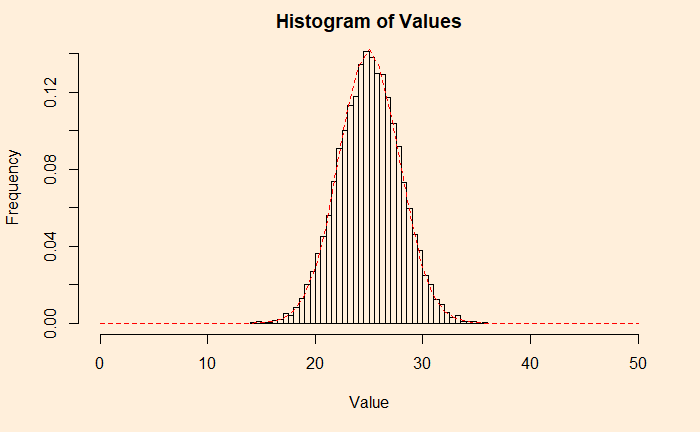
We will check some not-so-uniform distributions next.
Watch the Lecture by Nassim Taleb
The Central Limit Theorem Reloaded Read More »
You may have heard about the Pareto principle or the 80:20 rule. It is used in several fields and sounds like: 80% of actions come due to 20% of reasons or 80% returns from 20% of efforts etc.
Pareto distribution is a form of power-law probability distribution used to describe several phenomena. In R, dpareto describes the probability density function and ppareto, the cumulative distribution function.
Let’s work out an example. Suppose the salaries of workers obey a Pareto distribution with a minimum wage of 1000 and the so-called shape factor, alpha = 3. What is the mean salary, and what is the percentage of people who earn more than 2000?
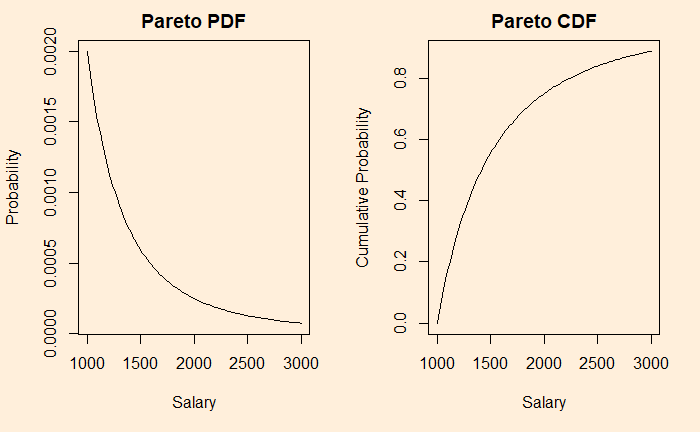
The Median is when the cumulative probability hits 0.5. So, applying the function for solving x such that ppareto(x, shape=3, scale=1000) = 0.5. x comes out to be 1260. For the answer to the other question, you find out the inverse of CDF (or 1 – CDF), i.e., 1 – ppareto(2000, shape=3, scale=1000) = 0.125 = 12.5%.
Pareto Distribution Read More »
The Narwhal curve shows the gap between the actual progress (for the US) on renewables and what it takes to get under 2 oC. It is called Narwhal as the shape of the graph resembles the toothed whale. The term is associated with Professor Leah Stokes, who plotted the progress of the top two emitters (electricity and transportation) to become carbon-free in the US until now (about 1- 2% growth rate) to the rate that is required to meet the target of carbon-free electricity and transportation by 2035, which is more than 10%.

Last time, we made the analogy between Bayesian inference and selection by elimination. We have used definitive data and, therefore, bar plots. But in reality, data are far more messy and probabilistic. Like this:
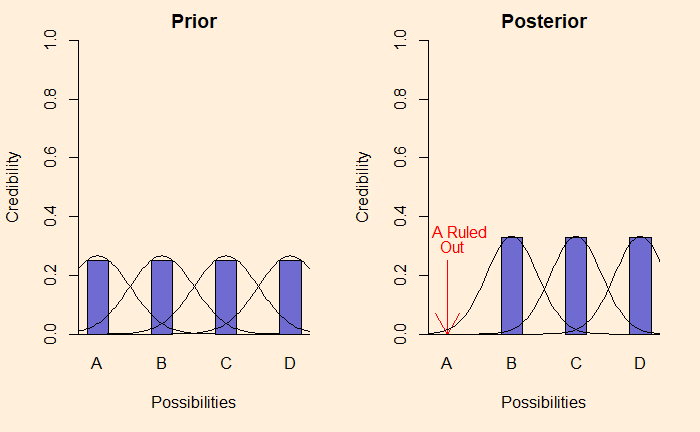
If these were describing productions from a factory, the distribution happens because of random variations of the product quality, variations of measurement etc.
Doing Bayesian Data Analysis by John K. Kruschke
Bayesian inference – Probabilistic View Read More »