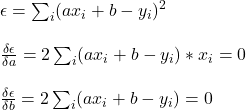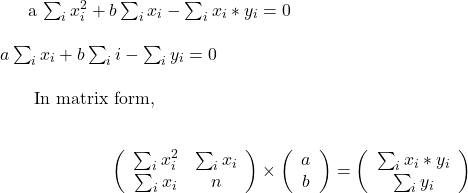Data & Statistics

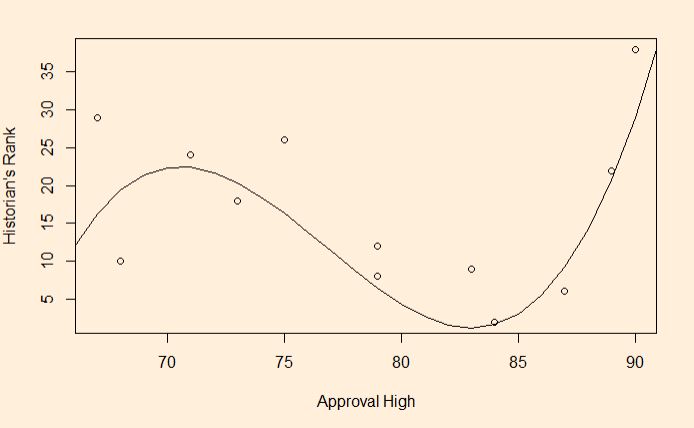
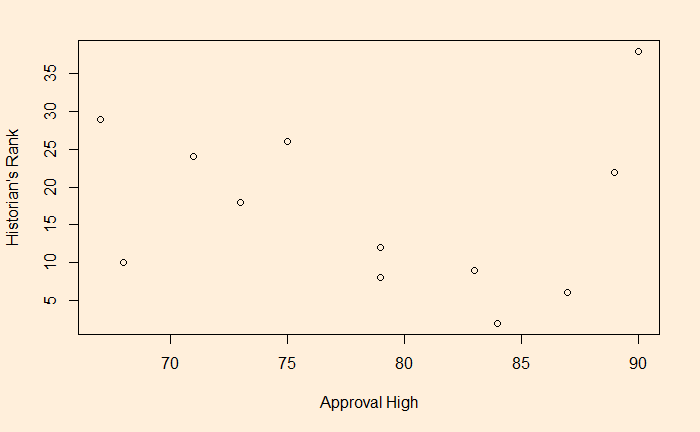
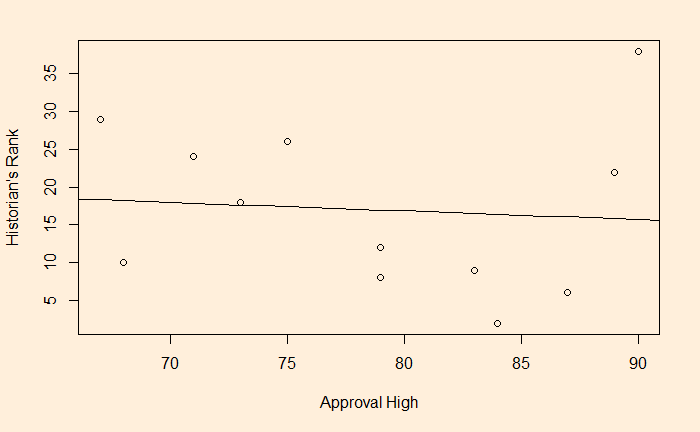
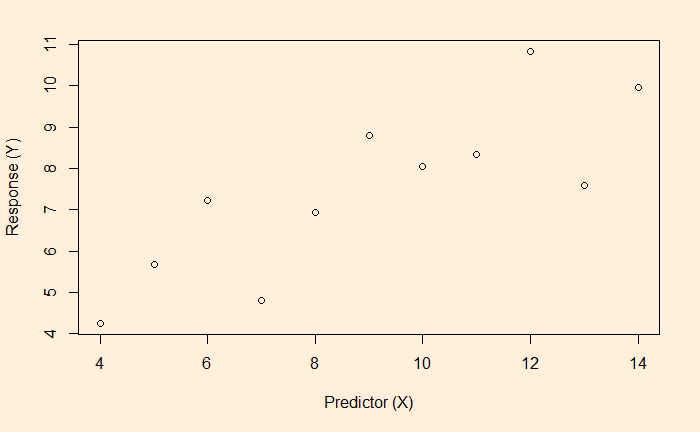
The foundation of predictive R-squared is cross-validation. We will examine the LOOCV method in this post. First, the data set that we used in the past exercises.

Then,

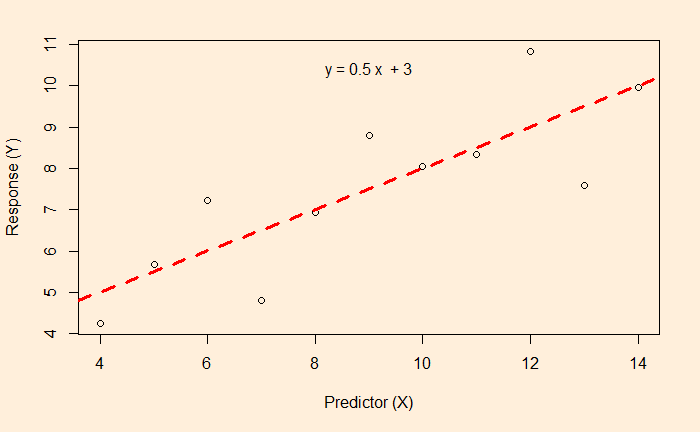
• The first row is removed from the list, and the regression model is developed with the other 11 data (2:12)
• The model is used to predict observation 1 (y). By plugging in the x value (e.g. 2) in the formula (cubic form)
• The predicted y is subtracted from the actual y for observation 1 and squared (called the squared residual)
• Observation 1 is returned to the list, and observation 2 is removed (1, 3:12)
• The process is continued until the last observation and squared residual are collected
• Sum all the squared residual to get what is known as PRESS (predicted residual error sum of squares)
• Predicted R² = 1 – (PRESS/TSS)

res_sq <- 0
for (i in 1:12) {
  new_presi <- Presi_Data[-i,]
  model1 <- lm(new_presi$Historians.rank ~ new_presi$Approval.High +  I(new_presi$Approval.High^2) + I(new_presi$Approval.High^3))
  
  res <- Presi_Data[i,1] - (model1$coefficients[1] + model1$coefficients[2]*Presi_Data[i,2]+model1$coefficients[3]*Presi_Data[i,2]^2 +model1$coefficients[4]*Presi_Data[i,2]^3)
  
    res_sq <- res_sq + res^2
}
res_sq

The res_sq is PRESS.

TSS (or SST) is the total sum of squares = sum of (response (y) – mean of response)²

sum((Presi_Data$Historians.rank-mean(Presi_Data$Historians.rank))^2)

predict_r_sq <- 1 - (res_sq/sum((Presi_Data$Historians.rank-mean(Presi_Data$Historians.rank))^2))

Last time we fitted a set of data using the cubic function.

Let’s analyse the quality of the fit using the predicted R-squared method. It is also called Leave-Out-One Cross Validation (LOOCV). What it does is that it systematically leaves out one data at a time and estimates how the model performs under those circumstances. For a good fit, the predicted R-squared should be high (as close to 1).

We will estimate the predicted R-squared of the dataset using the library, “olsrr“.

library(olsrr)
model <- lm(Presi_Data$Historians.rank ~ Presi_Data$Approval.High +  I(Presi_Data$Approval.High^2) + I(Presi_Data$Approval.High^3))

ols_pred_rsq(model)

The answer is -0.2, which suggests that the cubic function is overfitting the observation.

A usual tendency in regression is to chase better R-squared by increasing the dependent variables and ending up overfitting. Overfitting is a term used when your model is too complex that it sharts fitting noise. An example is this dataset taken from Regression Analysis Book by Jim Frost. It describes the highest approval ratings of the US presidents and their rank by historians.

First, we try out linear regression and check the goodness of fit.

lm(Presi_Data$Historians.rank ~ Presi_Data$Approval.High)

The R-squared value is close to zero (0.006766). Now, we try cubic fit.

model <- lm(Presi_Data$Historians.rank ~ Presi_Data$Approval.High +  I(Presi_Data$Approval.High^2) + I(Presi_Data$Approval.High^3))

But with an impressive R-squared (0.6639)

Now, try thinking how one can explain this complex relationship, i.e. Historians Rank = -9811 + 388.9 x Approval High -5.098 x Approval High^2 + 0.02213 x Approval High^3!

We have seen linear regression last time. While fitting a line could be a good start, one needs to exercise care before choosing it as the default. For example, see the plot below.

It gives the relationship between body mass index and body fat percentage, taken from Regression Analysis Book by Jim Frost. Warning: I’m not sure if the data was simulated or data.

Check what happens if you try and fit a straight line!

fit<-lm(BMI_Data$X.Fat ~ poly(BMI_Data$BMI,2,raw=TRUE))
quadratic = fit$coefficient[3]*BMI_Data$BMI^2 + fit$coefficient[2]*BMI_Data$BMI + fit$coefficient[1]

lines(BMI_Data$BMI,fit$coefficient[3]*BMI_Data$BMI^2 + fit$coefficient[2]*BMI_Data$BMI + fit$coefficient[1], col="red", type = "p")

OLS is the short form for ordinary least squares and is a linear regression method. The process is also known as curve fitting informally. The objective is to find the relationship between the dependent (the y) and independent (the x) variables; one eventually gets (to predict) the variation of y from the variation of x. In case you forgot, here is the scatter plot of the data.

We start with the equation of a line; because we fit a line (linear regression).

Now, the equation for the residuals, i.e. deviations of actual y from the model y.

As you’ve already guessed, square the residuals, sum them and find the values of the constants, a and b, that minimise the sum.

The above equations lead to two sets of linear equations that need to be solved.

We solve this equation for a and b using the following r code

Q1 <- data.frame("x" = c(10, 8, 13, 9.0, 11.0, 14.0, 6.0, 4.0, 12.0, 7.0, 5.0), "y" = c(8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68))

x_i_2  <-  sum(Q1$x*Q1$x)
x_i  <-  sum(Q1$x)
nn <- nrow(Q1)

x_i_y_i <- sum(Q1$x*Q1$y)
y_i <- sum(Q1$y)


X <- matrix(c(x_i_2, x_i, x_i, nn), 2, 2, byrow=TRUE)
y <- c(x_i_y_i,y_i)

solve(X, y)

We get a = 0.5 (slope) and b = 3.0 (intercept). Now use the shortcut R code (“lm“) to verify

mm <- lm(Q1$y ~ Q1$x)

summary(mm)

Call:
lm(formula = Q1$y ~ Q1$x)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.92127 -0.45577 -0.04136  0.70941  1.83882 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   3.0001     1.1247   2.667  0.02573 * 
Q1$x          0.5001     0.1179   4.241  0.00217 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.237 on 9 degrees of freedom
Multiple R-squared:  0.6665,	Adjusted R-squared:  0.6295 
F-statistic: 17.99 on 1 and 9 DF,  p-value: 0.00217

The original scatter plot with the model line included