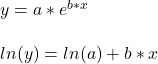Data & Statistics

Regression – Stock Index Performance

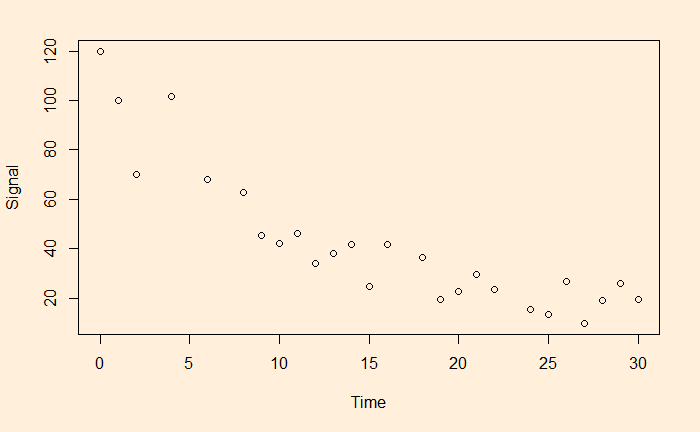
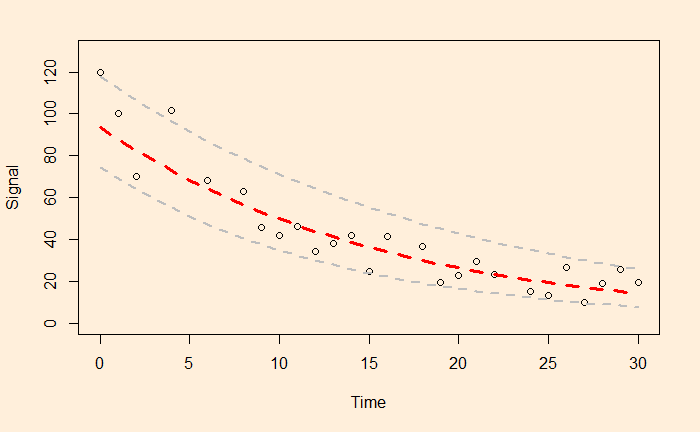
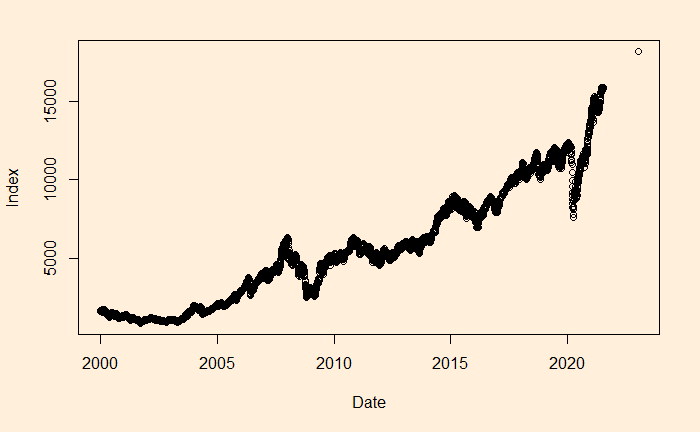
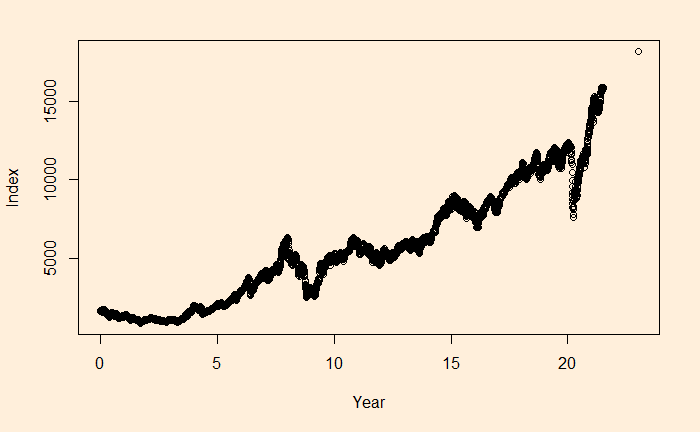
We will continue the regression, and this time, we’ll apply it to stock market performance. Below is the weighted average performance of the top 50 stocks listed in India’s National Stock Exchange, known as the NIFTY 50 benchmark index.

We want to perform regression of the data using a power law approximation of the following form.

\text{Index} = \text{Index}_0 * (1 + r) ^{Year}

There is a reason to write the function in the above format, as the constant r value can represent the underlying stocks’ average CAGR (compound annual growth rate). Before we proceed, let’s convert the x-axis to time (in years) using the following R code.

Nif_data$Year <- time_length(difftime(Nif_data$Date, Nif_data$Date[1]), "years")

The function “time_length()” comes from the “lubridate” package.

We’ll transfer the function to linear form and do an OLS fit.

ln(\text{Index}) = ln(\text{Index}_0) + Year * ln(1 + r)

The slope of this has to be ln(1+r) and intercept be ln(index0)

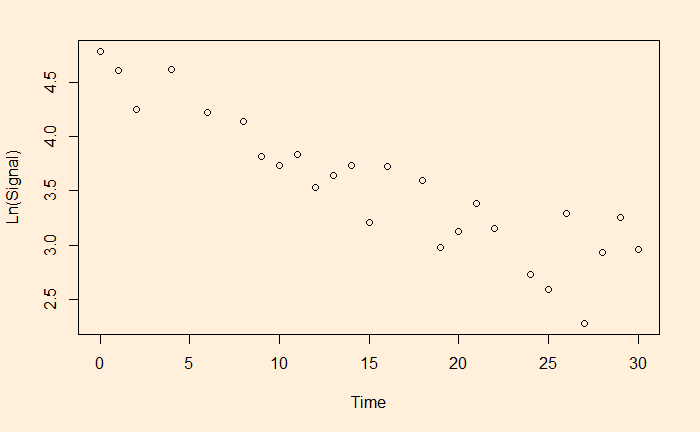
Nif_data$ln <- log(Nif_data$Index)
plot(Nif_data$Year, Nif_data$ln, xlab = "Year", ylab = "Ln(Index)")
abline(lm(Nif_data$ln ~ Nif_data$Year), col = "red", lty = 2, lwd = 3)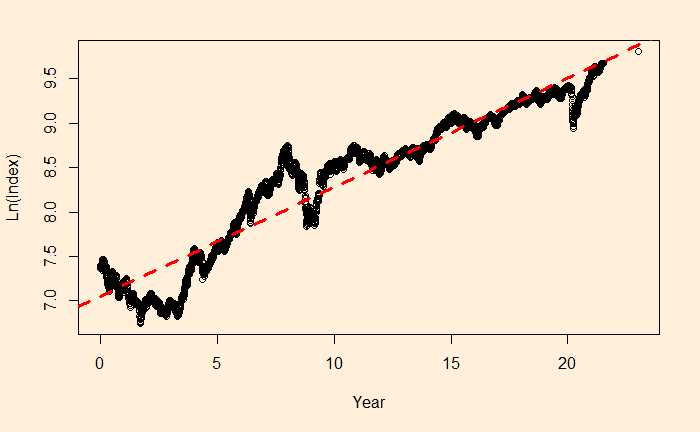
fit <- lm(ln ~ Year, data=Nif_data)
summary(fit)

Call:
lm(formula = ln ~ Year, data = Nif_data)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.62561 -0.11342 -0.02233  0.15665  0.71261 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7.0476743  0.0063781  1105.0   <2e-16 ***
Year        0.1230505  0.0005146   239.1   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2341 on 5352 degrees of freedom
Multiple R-squared:  0.9144,	Adjusted R-squared:  0.9144 
F-statistic: 5.718e+04 on 1 and 5352 DF,  p-value: < 2.2e-16

Converting them back, Index0 = exp(7.0476743) = 1150.181 and r = exp(0.1230505) – 1 = 0.1309415 or 13.09%.

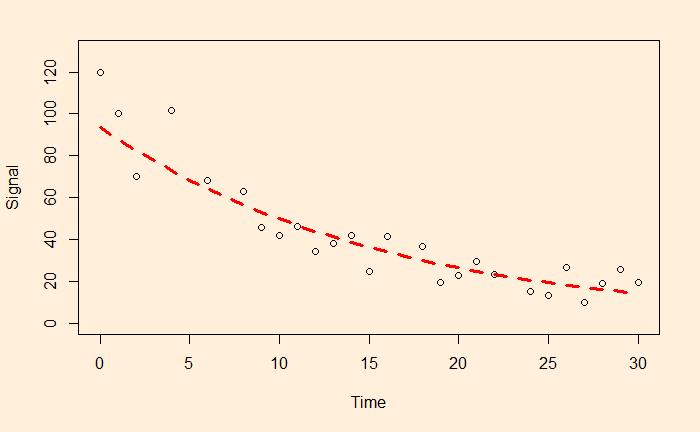
xx <- seq(0,30)
plot(Nif_data$Year, Nif_data$Index, xlim = c(0,30), ylim = c(0,19000), xlab = "Year", ylab = "Index")
lines(xx, exp(fit$coefficients[1])exp(fit$coefficients[2]xx), col = "red", lty = 2, lwd = 3)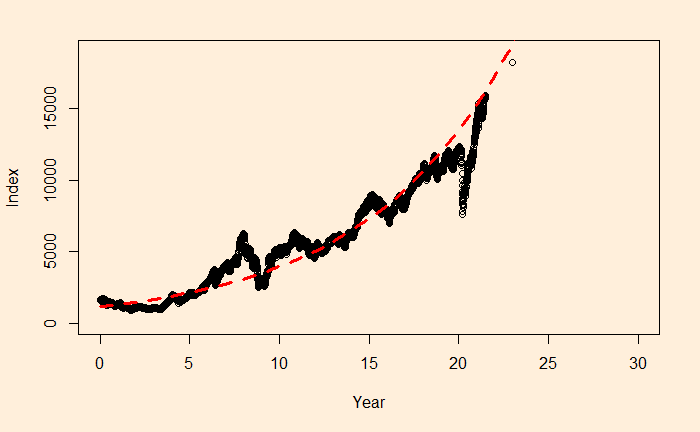

Obviously, this is an approximate estimation of the CAGR. If you want an accurate value, use the direct formula (Indexfin/Indexini)(1/Year) – 1

(Nif_data$Index[5354]/Nif_data$Index[1])^(1/Nif_data$Year[5354]) - 1

which gives 0.1117364 or 11.17%

The main reason for such a discrepancy (a 2% difference is a big deal for long-term compounding) between the two estimates is the less accurate intercept of regression. The actual intercept or index0 is 1592.20, which is so different from the estimated value of 1150.181.

Regression – Stock Index Performance Read More »

Regression – Exponential Curve

We have seen linear and non-linear regressions in the past. One type of non-linear function is exponential. A familiar example is the decay of a signal with time.

The easy way to perform the curve-fitting is to convert the exponential function to linear and perform an ordinary least square (OLS).

\\ y = a * e^{b*x} \\ \\ ln(y) = ln(a) + b*x

This is a linear function with slope = b and intercept = ln(a).

Let’s run a regression with these transformed variables.

df$ln <- log(df$Signal)
fit <- lm(ln ~ Time, data=df)
summary(fit)

Gives the output as 

Call:
lm(formula = ln ~ Time, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.55119 -0.17134  0.03271  0.19116  0.54713 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  4.540757   0.110923   40.94  < 2e-16 ***
Time        -0.063229   0.006115  -10.34 2.55e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2795 on 24 degrees of freedom
Multiple R-squared:  0.8167,	Adjusted R-squared:  0.809 
F-statistic: 106.9 on 1 and 24 DF,  p-value: 2.552e-10

a = e4.540757 and b = -0.063229 and here is the plot of data along with the fitted curve.

xx <- seq(0,30)
plot(df$Time, df$Signal, xlim = c(0,30), ylim = c(0,130), xlab = "Time", ylab = "Signal")
lines(xx, exp(fit$coefficients[1])*exp(fit$coefficients[2]*xx), col = "red", lty = 2, lwd = 3)

The next step is to get the confidence interval by running the confint() function.

conf_int <- confint(fit, level=0.95)

                  2.5 %      97.5 %
(Intercept)  4.31182187  4.76969119
Time        -0.07585068 -0.05060753

Incorporate them into the plot, and you get

xx <- seq(0,30)
plot(df$Time, df$Signal, xlim = c(0,30), ylim = c(0,130), xlab = "Time", ylab = "Signal")
lines(xx, exp(fit$coefficients[1])*exp(fit$coefficients[2]*xx), col = "red", lty = 2, lwd = 3)
lines(xx, exp(conf_int[1])*exp(conf_int[2]*xx), col = "grey", lty = 2, lwd = 2)
lines(xx, exp(conf_int[3])*exp(conf_int[4]*xx), col = "grey", lty = 2, lwd = 2)

Regression – Exponential Curve Read More »

Hindsight Narratives

Following are the grades (out of 10) of five students in three exams they did in a year.

Exam 1
(Jan)		Exam 2
(May)		Exam 3
(Sept)
Student 1457
Student 2345
Student 3636
Student 4576
Student 5753

Here are some of the reasons why they performed in that fashion.

The analysis

Student 1 is the star of the class. She comes from a middle-class family and is very hard-working and strategic. She had to overcome a series of adverse events in the year, but her perseverance earned her good grades.

Student 2 is an average one who comes from a financially average family, often distracted due to his habit of playing video games. Despite the backlashes, his hard work helped him to overcome the final hurdle.

Student 3 is the most confident young man, but at times overconfident, and that proved his downfall in the middle of the year. But he bounced back toward the end to show his true talent. Form may be temporary, but class is permanent.

Student 4 is intelligent but inconsistent. He was a bit unlucky earlier this year due to family issues, but he overcame those and became a decent performer.

Student 5 comes from an average family, and he lost his focus due to various family issues, including a breakup.

The narrative fallacy

The situation mentioned above is an example of what is known as the narrative fallacy. In reality, the scores you have seen above are the outcome of a coin-flipping exercise, and the points scored are the number of heads in the game. You may observe a few standard things within all those narratives that followed. They each present a compelling story. You will never see mentions of randomness or luck in it. They satisfy the audience’s thirst for the cause and effect of the event, i.e., the exam results. They all ignore things that didn’t fall into the storyline. The following table lists each student’s circumstances, and the highlighted words denote what has been cherry-picked by the author to tell her tale.

Student 1Confident, Financially OK, Video games, Hard working, Break up, Strategic, Inconsistent, Average
Student 2Confident, Financially OK, Video games, Hard working, Break up, Strategic, Inconsistent, Average
Student 3Confident, Financially OK, Video games, Hard working, Break up, Strategic, Inconsistent, Average
Student 4Confident, Financially OK, Video games, Hard working, Break up, Strategic, Inconsistent, Average
Student 5Confident, Financially OK, Video games, Hard working, Break up, Strategic, Inconsistent, Average

The investment gurus

The media is full of examples of narrative fallacies. Two classes of experts lead the table, namely the financial analysts and sports pundits.

Hindsight Narratives Read More »

Scoring Own Goals

Yesterday was a disastrous night for Leicester City’s Wout Faes, who scored not one, but two own goals for the opponents, Liverpool, that too at a time when his team was leading!

What is the probability?

A quick search online suggests that based on the last five seasons of the English Premier League for football, there is about a 9% chance of scoring an own goal in a match. Assuming the own-goals spread randomly as a Poisson distribution with an expected value (lambda) of 0.09 (9%), we can write down the following code a get a feel of how they distribute in e year. Note that there are 380 matches in a season.

plot(rpois(380,0.09), ylim = c(0,2), xlim = c(0,400), xlab = "Match Number", ylab = "Number of Own Goals", pch = 1)

The plot is just one realisation, and because the process is random, there are several possibilities of having own goals (0, 1, 2 or > 2) in a season.

1000th own goal last year

The following calculations are for the average number of own goals in the history of the premier league (the completed 30 seasons).

itr <- 10000

own_goal <- replicate(itr, {
epl <- rpois(380*27+420*3,0.09)
sum(epl > 0 )
})

mean(own_goal)
mean(own_goal)/30

The output below is not far off from what was observed (ca. 33 goals in a season and the 1000th goals scored last year).

991.0816
33.03605

How rare are two?

itr <- 10000

own_goal <- replicate(itr, {
epl <- rpois(380,0.09)
sum(epl == 2 )
})

mean(own_goal)

The expected value of having two own goals in a match is ca. 1.3 per season; for reference, the 2019-20 season had one occurrence.

Next, what is the expected value for two-own goals committed by one team?

epl <- rpois(380*2,0.09/2)

Extending it further: the probability of both goals being scored by the same player in a match becomes 0.09/20 (excluding the goalkeeper). The following code brings out the expected number of instances that a player scores two own goals in a match until the end of last season, i.e., 428 x 3 + 380 x 27 matches.

itr <- 10000

own_goal <- replicate(itr, {
epl <- rpois((380*27+420*3)*20,0.09/20)
sum(epl == 2)
})

mean(own_goal)

The answer is 2.3. The actual number stood at 3 at the end of last season (Jamie Carragher (1999, Liverpool vs Manchester United), Michael Proctor (2003, Sunderland vs Charlton) and Jonathan Walters (2013, Stoke vs Chelsea)).

References

How Common Are Own Goals:
1000 own goals: Guardian
Liverpool-Leicester City: BBC
Most Premier League own goals: The Sporting News
Premier League Stats

Scoring Own Goals Read More »

Poisonous Mushrooms

20% of mushrooms in a forest are red, 50% are brown, and 30% are white. A red mushroom has a 20% chance of being poisonous, whereas, for a non-red, it is 5%. What is the probability that a poisonous mushroom is red?

We have applied Bayes’ rule several times previously to solve similar problems. So straight to the equation.

\\ P(R|P) = \frac{P(P|R)*P(R)}{P(P|R)*P(R) + P(P|nR)*P(nR)} \\ \\ P(R|P) = frac{0.2*0.2}{0.2*0.2 + 0.05*0.8} = 0.5

P(R|P) = Probability of red mushroom given that it is poisonous
P(P|R) = Probability of poisonous mushroom given that it is red = 0.2
P(R) = Prior probability of finding a red mushroom = 0.2
P(P|nR) = Probability of poisonous mushroom given that it is not red = 0.05
P(nR) = 0.5 + 0.3 = 0.8

Poisonous Mushrooms Read More »

Running t-Test on a Sample

We have been hearing about hypothesis testing a lot. But what is that in reality? We will resolve it systematically by working with samplings from a large – computer-generated – population.

What is hypothesis testing?

It is a tool to express something about a population from its small subset, known as a sample. If one measures the heights of 20 men in the city centre, does something with the data and makes a claim about men in the city, it qualifies as a hypothesis. Imagine if it was a cunning journalist who measured the heights (mean = 163 cm and standard deviation = 20 cm) and reported that the people in the city were seriously undersized (the national average is 170), a claim the mayor vehemently disputes.

So, we need someone to perform a hypothesis test assessing two mutually exclusive arguments about the city’s population and tell which one has support from the data. The mayor says the average is 170, and the journalist says it’s not.

The arguments

Null hypothesis: The population mean equals the national average (170 cm).
Alternate hypothesis: The population mean does not equal the national average (170 cm).

Build the population

The city has 100,000 men, and their height data is available to an alien. The average is, indeed, 170 cm. And do you know how she got that information? By running the following R code:

n_pop <- 100000
pop <- rnorm(n_pop, mean = 170, sd = 17.5)

Don’t you believe it? Here they are:

The journalist took a sample of 30 from it. So the statistician’s job is to verify if his number (sample mean of 163 cm at sample standard deviation of 20 cm) is possible from this population.

Test statistic

Calculating a suitable test statistic is the first step. A statistic is a measure that is applied to a sample, e.g., sample mean. If the same is done to a population, it is called a parameter. So population parameters and sample statistics. For the given task, we chose a t-test statistic by smartly combining the mean and standard deviation of the sample into a single term in the following fashion:

t = \frac{\bar{X} - \mu_0}{s/\sqrt{n}}

X bar is the sample mean
mu0 is the null value
s is the sample standard deviation and
n is the number of individuals in the sample

For the present case, it is:

t = \frac{163 - 170}{20/\sqrt{30}} = -1.92

Why is that useful?

To understand the purpose of the t-test statistics, we go back to the alien. It collected 10,000 samples, 30 data points at a time, from the population, and here is how it was obtained.

itr <- 10000

t_val <- replicate(itr, {
n_sam <- 30
sam <- sample(pop, n_sam, replace = FALSE)
t_stat <- (mean(sam) - 170)/(sd(sam) / sqrt(n_sam)) 
})

You can already suspect that our t-value of -1.92, obtained from an average of 163 cm, is not improbable for a population average of 170 cm. In other words, getting a sample mean of 163 is “natural” within the scatter (distribution) of heights. If you are not sure how t-values change, try substituting 162, and you get -2.2 (higher magnitude, further away from the middle).

t-distribution

Luckily, there has been a standard distribution that resembles the above histogram created from the subsamples. As per wiki, the t-distribution was first derived in 1876 by Helmert and Lüroth. It is of the following form. 

f(t) = \frac{\Gamma(\frac{df + 1}{2})}{\sqrt{df\pi} \Gamma(\frac{df }{2})} (1 + \frac{t^2}{df})^{-\frac{(df + 1)}{2}}

The beauty of this function is that it has only one parameter, df (number of data points – 1). The plot of the function for df = 29 is below.

x_t <- seq(- 5, 5, by = 0.01)
df <- 29

y_t <- gamma((df+1)/2)(1+(x_t^2)/df)^(-(df+1)/2)/(sqrt(df*3.14)*gamma(df/2))

plot(x_t, y_t, type = "l", main = "t-distribution for df = 29", xlab = "t value", ylab = "f(t)")

Combining distributions

Before going forward with inferences, let’s compare the sampling distribution (from 10000 samples as carried out by the alien) with the t-distribution we just evaluated.

Pretty decent fitting! Although, in reality, we never get a chance to produce the sampling distribution (the histogram), we do not need that anymore as we are convinced that the t-distribution will work instead.

Verdict of the test

The t-statistic derived from the sample, -1.92, is within the distribution if the average height of 170 cm is valid for the population. But by how much? One way to specify an outlier is by agreeing on a significance value; the statistician’s favourite is 95%. It means if the t value of the sample (the value of the x-axis) is in such a way that it is part of 95% of the distribution, then the sample mean that produced the t-value is valid. In the following figure, the 95% coverage is shaded, and our statistic is denoted as a red dot. In summary: a value of 163 cm is perfectly reasonable in the universe of 170!

Based on this, the collected data is not sufficient to dislodge the null hypothesis – a temporary respite for the mayor. Interestingly, the data can never prove he was right – it only says there is insufficient ground to reject his position.

Running t-Test on a Sample Read More »

Hypothesis Tests – What to Use

We have seen several hypothesis testing methods, such as t-tests, Z-tests, ANOVA etc. Today, we will build a flowchart to help decide what to choose. Before we select, there are a few conditions that we must satisfy.

1) We have a random sample. In case you forgot, a sample is a collection of observations. If all members are inside it, you no longer call it a sample but a population. So, the first condition says the observations must be unbiased.
2) We focus on continuous data this time.
3) The sample data should follow a normal distribution. If not, have more than 30 observations and let the central limit theorem justify you.

What is a paired sample?

Paired samples are observations on the same set of individuals, e.g. before and after or pre-intervention and post-intervention.

Hypothesis Tests – What to Use Read More »

Coin Flipping Game

Anna and Bryce are playing a game of coin flips. Anna gets one point for a head, and Bryce gets one for a tail. Whoever secures 10 points win the game. At present, Anna leads 8 – 7. What is the probability that she eventually wins?

The maximum number of games possible from now is four (a best of 19 will lead to 10, and 15 games are over). The simplest solution is to list all the possibilities that favour Anna and estimate the probabilities of those occurrences. They are

OutcomeProbability
HH 1/4
HTH 1/8
HTTH1/16
THH 1/8
TTHH1/16
THTH1/16
Total11/16 = 0.6875

Coin Flipping Game Read More »

Girl Paradox – The Simulations

You may recall the boy or girl paradox and the Bayesian explanation from the earlier two posts. Today we will perform experiments with thousands of families and count. Or simulate using the Monte Carlo method written in R. First, what is the paradox?

1) Mr X has two children. The first one is a girl, and what is the probability that both the children are girls?
2) Mr Y has two children. At least one of them is a girl, and what is the probability that both the children are girls?

Martin Gardner (1959)

We will use the replicate() function to do simulations. Before we go through the problems, let’s calculate the probability of having two girls if no other information is given.

itr <- 1000000

girl_count <- replicate(itr, {
   child <- sample(c("B","G"), size = 2, replace = TRUE, prob = c(1/2,1/2))
   child <- paste(child,collapse =" ")
    ifelse (child == "G G", "2G", "n2G") 
})

length(girl_count[girl_count == "2G"]) / length(girl_count[girl_count == "2G" | girl_count == "n2G"])

The code yields 0.25 as the answer. To explain what we did: assign “B” or “G” to two children at random using the sample() function and count the items “G G” among all the possible outcomes. Now, item 1 of the two.

itr <- 1000000

girl_count <- replicate(itr, {
    child <- sample(c("B","G"), size = 2, replace = TRUE, prob = c(1/2,1/2))
    child <- paste(child,collapse =" ")

    if(substr(child, 1, 1) == "G"){
       ifelse (child == "G G", "2G", "1G") 
    } 
})

length(girl_count[girl_count == "2G"]) / length(girl_count[girl_count == "2G" | girl_count == "1G"])

The answer is 0.5. The key difference here is that we count for two girls for only the situations where the first one is already a girl. It is achieved by searching the first member of the substring and proceeding further only if it is a “G”. Note: using the function substr() requires the library(stringr). Finally, the contentious one – item 2.

itr <- 1000000

girl_count <- replicate(itr, {
   child <- sample(c("B","G"), size = 2, replace = TRUE, prob = c(1/2,1/2))
   child <- paste(child,collapse =" ")

   if(grepl("G", child, fixed = TRUE)){
      ifelse (child == "G G", "2G", "1G") 
   } 
})

length(girl_count[girl_count == "2G"]) / length(girl_count[girl_count == "2G" | girl_count == "1G"])

The answer, and no surprise, is 0.33. We have used the grepl() command to find a G somewhere as the trigger to further count or not.

Tailpiece

For those who suspect my previous post about throwing dice for a double six was similar to the last one: You are right; change B and G to the sides of a die, run the simulation, and you get what you solved analytically.

itr <- 1000000

dice_count <- replicate(itr, {
  dice <- sample(c("1","2", "3", "4", "5", "6"), size = 2, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))
  dice <- paste(dice,collapse =" ")

if(grepl("6", dice, fixed = TRUE)){
  ifelse (dice == "6 6", "2-6", "1-6") 
  } 
})

length(dice_count[dice_count == "2-6"]) / length(dice_count[dice_count == "2-6" | dice_count == "1-6"])

Girl Paradox – The Simulations Read More »

It’s Raining Dice

Back to dice. Your friend casts two dice and tells you that at least one of them is a six. What is the probability that both of them are sixes?

We use Bayes’ theorem first.

P(B6|A6) = \frac{P(A6|B6)*P(B6)}{P(A6|B6)*P(B6) + P(A6|F6)*P(F6) + P(A6|S6)*P(S6) + P(A6|N6)*P(N6)}

P(B6|A6) – Probability of both six, given at least one is a six.
P(A6|B6) – Probability at least one is a six given both are six = 1
P(B6) – Prior probability for both of them is six = 1/36.
P(A6|F6) – Probability at least one is a six, given the first die is a six (and the second is not) = 1
P(F6) – Prior probability of the first die is a six (and the second is not) = (1/6)x(5/6).
P(A6|S6) – Probability at least one is a six, given the second die is a six (and the first is not) = 1
P(S6) – Prior probability of the second die is a six (and the first is not) = (1/6)x(5/6).
P(A6|N6) – Probability at least one is a six given none is size = 0
P(N6) – Prior probability of none is a six = (5/6)x(5/6).

P(B6|A6) = \frac{\frac{1}{36}}{\frac{1}{36} + \frac{5}{36} + \frac{5}{36} + 0} = \frac{1}{11}

If you are not convinced, here is a pictorial explanation:

Here are all the pairs that include at least one of them as a six. There are 11 of them in total. And there is only one that is both six. So the probability is 1 in 11.

It’s Raining Dice Read More »