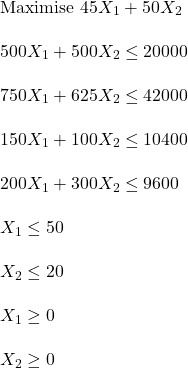Linear Programming in R – What If

In the last post, we did the optimisation of a product line and found that:
The maximum profit is 1880, and the optimal production quantities are alpha = 24 and beta = 16.

Now, a question can arise:
What if we change the objective or the constraints by a little? In other words, how sensitive is the solution to changes in the situation?

One way is to rerun the program with a different coefficient. Let us change alpha’s profit (per kg) from 45 to 47 and see what happens.

library(lpSolve)
f.obj <- c(47, 50)
f.con <- matrix (c(500, 500, 750, 625, 150, 100, 200, 300, 1, 0, 0, 1), nrow = 6, byrow = TRUE)
f.dir <- c("<=", "<=")
f.rhs <- c(20000, 42000, 10400, 9600, 50, 30)

results <- lp ("max", f.obj, f.con, f.dir, f.rhs)
results
results$solution
Success: the objective function is 1928 
24 16

The maximum profit changes to 1928, but the optimal production quantities remain at (24, 16).

What about making it 50? Now, quantities change to (40,0) – produce only alpha!

Rather than making changes manually, the lp function can do it for us using the attribute compute.sens = TRUE . We then use results$sens.coef.from and results1$sens.coef.to to get the range of coefficients.

results <- lp ("max", f.obj, f.con, f.dir, f.rhs, compute.sens=TRUE)
results1$sens.coef.from
results1$sens.coef.to
33.33333 45.00000
50.0 67.5

The solution is optimal as long as the coefficient on X1 stays between [33.33 and 50].
The solution is optimal if the coefficient on X2 is between [45 and 67.5].
Note that you only change one coefficient at a time in sensitivity calculations.

Linear Programming in R – What If Read More »

Linear Programming in R

A factory makes two products, Alpha and Beta, using four ingredients: A, B, C and D. The quantity requirement for each component per kg of the product is:

ABCD
Alpha500750150200
Beta500625100300

The profits from the products (per kg) are

Profit
Alpha45
Beta50

The maximum daily demands for the product (kg) are:

Profit
Alpha50
Beta20

If there are constraints (as below) on the supply of the ingredients, what should be the product mix?

ABCD
2000042000104009600

Linear Programming

This is an example of the application of linear programming (LP), a popular tool in prescriptive analysis. The solution starts by identifying the decision variables and the objective function.

The quantities of the two products are the decision variables. Let’s name them X1 (alpha) and X2 (beta). The objective (function) is to maximise the profit, 45 X1 + 50 X2. All the other information provided above are constraints (on the ingredients, demand, etc). The LP formulation is given below:

\\ \textrm{Maximise } 45 X_1 + 50 X_2 \\ \\ 500 X_1 + 500 X_2 \le 20000 \\ \\ 750 X_1 + 625 X_2 \le 42000 \\ \\ 150 X_1 + 100 X_2 \le 10400 \\ \\ 200 X_1 + 300 X_2 \le 9600 \\ \\ X_1 \le 50 \\ \\ X_2 \le 20 \\ \\ X_1 \ge 0 \\ \\ X_2 \ge 0

We use R to solve the set of equations. The package used is ‘lpSolve’.

library(lpSolve)
f.obj <- c(45, 50)
f.con <- matrix (c(500, 500, 750, 625, 150, 100, 200, 300, 1, 0, 0, 1), nrow = 6, byrow = TRUE)
f.dir <- c("<=", "<=")
f.rhs <- c(20000, 42000, 10400, 9600, 50, 30)

results <- lp ("max", f.obj, f.con, f.dir, f.rhs)
results
results$solution
Success: the objective function is 1880 
24 16

The maximum profit is 1880, and the optimal production quantities are alpha = 24 and beta = 16.

Linear Programming in R Read More »

More Dice Roll

We will consider three instances of utilising the concept of expected values for estimating the number of trials for a given outcome.

Getting a 6

How many times must a 6-sided fair die be rolled for a 6?

There is a 1 in 6 chance that the expected number of rolls is 1, i.e., get a six in the first roll. There is a 5/6 chance that the roll results in another number. In that case, the game will need at least another toss, and the game will repeat. Let E be the expected number of rolls until a 6, using the expected value formula:
E = (1/6)x1 + (5/6) x (E+1)
E = 1 + 5E/6
E = 6

Getting a 66

How many times must a 6-sided fair die be rolled for a 6 followed by a 6?

Let E66 be the required value. We have seen in the earlier section that the expected number of rolls for a six is 6. Once that happens, there is a (1/6) chance that the next roll will give a six and a (5/6) chance that the game will start again.
E66 = 6 + (1/6)x1 + (5/6) x (E66+1)
E66 = 6 + 1 + 5E66/6
E66 = 42

Getting a 65

Here, we estimate the expected number of rolls for a six followed by a number other than six. It is more complicated than the earlier case. After getting the first 6, there are three possibilities:

  1. A 5 and game over.
  2. A 6 and have another chance for a 65 (665).
  3. A number other than 5 or 6 and restart. 

Let E65 be the required value, the expected number of rolls for 65 from the start. We will need to define another term, E6, which is the expected number of rolls for 65 from 6.

E6 = (1/6)x(E6+1) + (4/6)x(E65+1) + (1/6)x1
E65 = (1/6)x(E6+1) + (5/6)x(E65+1)

E65 = 36

More Dice Roll Read More »

Dice Roll, Again

A pair of dice is thrown twice. What is the probability that the faces of the second throw are the same as the first?

Two types of outcomes are possible when you throw a pair of dice. In the first case, both dice show the same number (11, 22, 33, 44, 55, 66). In the second type, they differ (12, 13, etc.). We solve both scenarios separately.

Different

For a pair of dice, there are a total of 6 x 6 = 36 events possible. Of these, 6 are the same type (11, 22, 33, 44, 55, 66), and 36 – 6 = 30 are different. The probability of different numbers is 30/36.
When you repeat the throw, the exact two numbers come only in 2 out of the 36 outcomes. E.g., if 12 comes first, there are two ways of getting 12 in the second – 1 from the first die, 2 from the second OR 2 from the first or 1 from the second. The probability is 2/36.
The overall possibility of a repeat of pairs is (30/36)x(2/36)

Same

We have already seen that the probability of getting the same numbers in the first pair is 6 out of 36 (6/36). In the repeat, the situation only happens 1 in 36 (1/36).
The overall possibility of a repeat is (6/36)x(1/36)

We need to add the two probabilities to get the probability of getting the same in the repeat.

(30/36)x(2/36) + (6/36)x(1/36) = 0.0509; a 5% chance.

Dice Roll, Again Read More »

Principle of Inclusion-Exclusion – Applied

This time, we apply the inclusion-exclusion principle:
A fair die was rolled n times. What is the probability that at least 1 of the 6 values never appears?

The required probability is nothing but:
the probability of not getting a 1 OR
the probability of not getting a 2 OR
the probability of not getting a 3 OR
the probability of not getting a 4 OR
the probability of not getting a 5 OR
the probability of not getting a 6

P (A \cup B \cup C \cup D \cup E \cup F)

The probabilities are the same since it is a fair die (5/6).

Let’s apply the inclusion-exclusion principle:
1) Add all single probabilities: The probability of a given number missing in one roll = 5/6. All such single probabilities in n rolls = 6C1 x (5/6)n
2) Subtract all pair probabilities: The probability of the given two numbers missing in one roll = 4/6. All such pair probabilities = 6C2 x (4/6)n
3) Add all 3-tuple probabilities: The probability of the given three numbers missing in one roll = 3/6. All such pair probabilities = 6C3 x (3/6)n
4) Subtract all 4-tuple probabilities: The probability of the given four numbers missing in one roll = 2/6. All such pair probabilities = 6C4 x (2/6)n
5) Add all 5-tuple probabilities: The probability of the given five numbers missing in one roll = 1/6. All such pair probabilities = 6C5 x (1/6)n

6C1 x (5/6)n – 6C2 x (4/6)n + 6C3 x (3/6)n – 6C4 x (2/6)n + 6C5 x (1/6)n

For ten rolls, n = 10

n <- 10
choose(6,1) * (5/6)^n - choose(6,2) * (4/6)^n  +  choose(6, 3)* (3/6)^n - choose(6,4)*(2/6)^n + choose(6,5) * (1/6)^n
0.728

Similarly, for 20 rolls, there is a 0.15 chance of not getting at least one number.

Principle of Inclusion-Exclusion – Applied Read More »

Principle of Inclusion-Exclusion

We have seen the addition rule (OR Rule) of probabilities. It says
P (A OR B) = P(A) + P(B) – P (A AND B)

P (A \cup B) = P(A) + P(B) - P (A \cap B)

The above equation is a special case of the Principle of Inclusion-Exclusion (PIE). For the union of three events that are not necessarily disjoint:

\\ P (A \cup B \cup C) = P(A) + P(B) + P(C) \\ - P (A \cap B) - P (A \cap C)- P (B \cap C) \\ + P (A \cap B \cap C)

It goes by the sequence of adding and subtracting combinations of interactions.

P(A OR B OR C) =
Add all individual probabilities
subtract all pairs of probabilities (AND rule)
add all triplets of probabilities (AND rule), etc.

Let’s do an example to illustrate.

Principle of Inclusion-Exclusion Read More »

Poissonous Rain Drops

Raindrops are falling at a rate of 20 drops per inch per minute. What is the probability that no drop falls inside a 5-inch area for 3 seconds?

Since we consider the raindrops fall at random, we model this as a Poisson process. We need two parameters to estimate the required Poisson probability.
1) average rate of success: lambda
2) number of successes: s

Since we must consider zero success (s = 0) in a 3-second interval on a 5-inch area, we convert the success rate on the 5-inch area in 3 seconds.
lambda = 20 drops per inch per minute
= 20 x 5 = 100 drops per 5-inch area per minute
= 100/20 (= 5) drops per 5-inch area per 3 seconds

\\ P(X = s) = \frac{e^{-\lambda}\lambda^s}{s!} \\ \\ P(X = 0) = \frac{e^{-5}5^0}{0!} = 0.0067

OR

dpois(0, 100/20)

Poissonous Rain Drops Read More »

Probability of a Norepeatword

If one must make a random Norepeatword from the 26 alphabets, what is the probability of picking a work with all 26 letters? A Norepeatword is an assemblage of any number of alphabets (1 to 26) such that no letter is repeated. Let’s do the problem step by step.

  1. Number of 26 letter words: there are 26! words possible from 26 letters.
  2. Number of k-letter words (k = 1 to 26): It has two parts: A) how many k-letter words are possible from 26 and B) how many rearrangements are possible for each.
    A) 26Ck collections can be made from 26 letters with k letters.
    B) For each collection, k! rearrangements are possible.
    Therefore, the number of k-letter Norepeatwords is 26Ck x k!, and the total is obtained by summing from k = 1 to k = 26.

\textrm{\# norepeatwords} = \sum\limits_{k = 1}^{26} _{26}C_k * k! = \sum\limits_{k = 1}^{26} \frac{26!}{k!(26-k)!} * k!

The required probability is:

\\ P = \frac{26!}{\sum\limits_{k = 1}^{26} \frac{26!}{k!(26-k)!} * k!} = \frac{26!}{\sum\limits_{k = 1}^{26} \frac{26!}{(26-k)!}} = \frac{1}{\frac{1}{25!} + \frac{1}{24!} + ... + \frac{1}{1!} + 1}

The denominator of the equation is the famous Taylor series expansion of ex for x = 1.
ex = 1 + x + x2/2! + …

So, P = 1/e

Probability of a Norepeatword Read More »

All Three Girls

A family has six children – three boys and three girls. What is the probability that three older children are all girls?

Let’s label the children 1, 2, and 3 as girls and 4, 5, and 6 as boys. The required probability is nothing but:
The permutations for 1, 2, and 3 come up in the first three (any order) / All permutations
3! x 3! / 6! = 6/(6 x 5 x 4) = 1/20 = 0.05

Let’s use brute force and perform an R simulation.

itr <- 1000000

girl <- replicate(itr, {
   birth <- sample(seq(1:6), size = 3, replace = FALSE, prob = rep(1/6, 6))
   all_girl <- c(1,2,3) 

    if(all(all_girl %in% birth) == TRUE){
       counter <- 1
   } else {
       counter <- 0
   }
   
})
mean(girl)
0.050108

All Three Girls Read More »

Flipping for Winners

Sixty-four teams are playing a knockout tournament, and you have to predict the winners of each game. You get 1 point for correctly predicting the first-round winners, 2 for the second, 4 for the third, 8 for the fourth, 16 for the semi-finals and 32 for the final. If you flip coins to choose the winners, what is the expected number of points for predicting all the matches?

Round 1

The expected value of an event is the probability of occurrence x the payout. For a first-round match, the probability of predicting a single winner is (1/2), and the payout is 1.
The expected value for a single first round match = (1/2) x 1 = 1/2
Since there are 32 matches, the total expected value = 32 x 1/2 = 16

Round 2

The probability of predicting a winner in the second round means you need to get two coin flips right (first round and second round). The probability is (1/2) x (1/2). The Payoff is 2. The expected value is (1/2) x (1/2) x 2 = 1/2. For all the 16 matches in this round, it is 16 x 1/2 = 8.

Round 3

The probability is (1/2) x (1/2) (1/2). The Payoff is 4. The expected value is (1/2) x (1/2) x (1/2) x 4 = 1/2. Total = 8 x 1/2 = 4.

The next 3 rounds

The expected values for the next three rounds are 4 x 1/2, 2 x 1/2, and 1/2, respectively.

Adding all values: 16 + 8 + 4 + 2 + 1 + 1/2 = 31.5.

Flipping for Winners Read More »