May 2024

Bargaining Theory: Outside Options and Uncertainty

The ultimatum game continues between Annie and Becky. But there is a difference here.

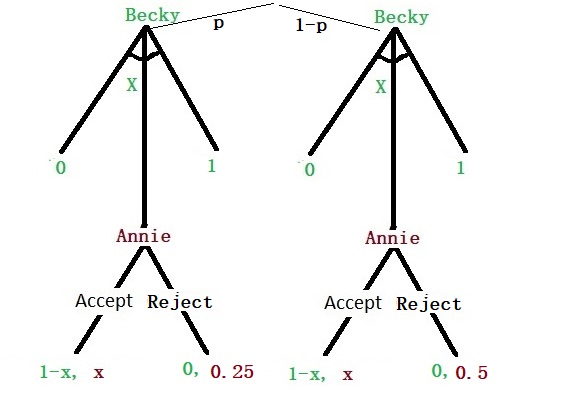
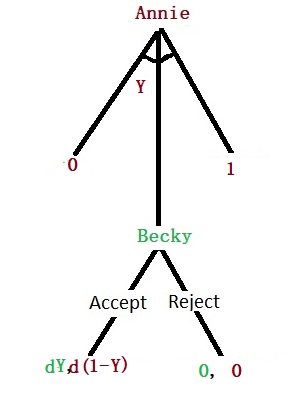
Like before, Becky is offering Annie a 0 to 1 division of the surplus, which Annie can accept or reject. However, instead of ending up with zero upon rejection, she has a payoff of 0.25 or 0.5 from an outside option. Unlike in earlier cases, Becky is uncertain about Annie’s bottom line. So, she attaches a probability p for 0.25 and (1-p) for 0.5. It means:

If Becky offers < 0.25, Annie rejects 100%
If Becky offers >/= 0.25 but < 0.5, Annie accepts with a probability p
If Becky offers >/= 0.5, Annie accepts 100%

If Becky offers 0.5, then her expected payoff is:
1 – 0.5 = 0.5

If Becky offers 0.25, then her expected payoff is:
p x (1-0.25) + (1-p) x 0 = 0.75 p

In other words, Becky should offer 0.25 if 0.75 p > 0.5 or p > 0.5/0.75 or p > 2/3

Bargaining 101 (#21): William Spaniel

Bargaining Theory: Outside Options and Uncertainty Read More »

Bargaining Theory – Alternating Offers

We have seen a single-stage – ultimatum – game and a two-stage game.

Ultimatum game

In the single-stage game, Becky makes the offer. As the game is over after stage 1, the earnings are:
Annie: 0
Becky: 1

Two-stage game

In the two-stage game, Becky calls the shots. In the end, as we have seen, Annie earns d and Becky 1-d.
Annie: d
Becky: 1-d

Three-stage game

What happens if there is a stage 3? This happened because Annie had rejected Becky’s offer in the second stage. Now, Becky is making the counteroffer. If Becky’s offer is rejected, Annie will get nothing, and Becky will take the entire surplus of 1.
Annie: 0
Becky: 1

Annie knows in the second stage itself that Becky will get the full value (discounted by d due to the time delay) if the game goes to the third. So, in the second stage, Annie must offer d to get Becky to accept the offer. Annie can take the remaining 1-d.
Annie: 1-d
Becky: d

Knowing what returns Annie will get in the second stage (1-d), Becky can offer d(1-d) from the beginning itself for Annie to accept.
Annie: d(1-d) = d – d2
Becky: 1 – d(1-d) = 1 – d + d2

Summary

GameOffer
by		Return
Annie		Return
Becky
1-stageBecky 0 1
2-stageAnnie d 1 – d
3-stageBecky d – d21 – d + d2

Extrapolating from the above pattern, we can say if the game was ending in stage 4, Annie would have made an offer and earned d – d2 + d3 and Becky would have ended up with 1 – d + d2 – d3

Bargaining Theory – Alternating Offers Read More »

Bargaining Theory – Counteroffer

We have seen the first level of bargaining – the ultimatum game. Becky made the offer for Annie’s car, and the latter will accept or reject it. The decision tree that we have seen before can be drawn as a fraction of the surplus:

In the next level, Annie can make a counteroffer instead of rejecting the offer. Here is the game:

The above picture suggests that Annie offers Becky a fraction of the surplus in her counteroffer. But there is a small problem. Since the counteroffer and the decision consume more time than the take-it-or-leave-it situation, the benefit from the subsequent game must be discounted (time value of money) by a fraction d.

Let’s solve the problem, as before, from the end backwards.

The solution is exactly like before, and the answer is that Annie will get the entire surplus, and Becky has no bargaining power. Here is the whole picture.

And to the start of the tree.

Now, Becky must decide what X should be, as she knows Annie can reject the offer and get a payoff of d. In that case, Becky will get zero. The solution that Annie accepts, therefore, is X = d. Annie is getting d, and Becky will get (1 – d) of the surplus.

Bargaining Theory – Counteroffer Read More »

Bargaining Theory – Take it or Leave It

Here, we see one of the bargaining strategies: the take-it-or-leave-it game, which you may know by another name: the ultimatum game.

Annie owns a car that she values at $8,000. Becky wants a car and values Annie’s car at $8500. In this game, Becky makes a single offer (ultimatum) on a price. Also, Becky knows how much Annie values the car. Annie will then accept (and sell) or reject the offer. In bargaining games, players always want to maximise their economic benefit. Here is the game tree of the situation.

Let’s see from the top. Becky is making offer X, between $0 and $8,500. The bottom part is what Annie will do—accept or reject. If Annie accepts, her payoff will be $X. Becky’s payoff will be the surplus—the difference between what she values and what she will pay to Annie. If Annie rejects, Becky will get nothing, and Annie will retain the car worth $8,000.

The problem is solved by backward induction. Annie has three choices on Becky’s offer.
X>$8000 – Annie accepts
X=$8000 – Annie is indifferent (case1: she rejects)
X<$8000 – Annie rejects.

Having built Annie’s choice, let’s work upward on Becky’s decision. So, if Becky decides to offer $8000 or below, her payoff will be zero.

On the other hand, Becky can offer X > $8000. Her payoff will vary but maximises at 499 if she offers $8000, one dollar more than the rejection level.

And Becky should just do that.

Bargaining Theory – Take it or Leave It Read More »

Bargaining Theory

As per John Nash, “a two-person bargaining situation involves two individuals who have the opportunity to collaborate for mutual benefit in more than one way”. The problem can be considered a nonzero-sum two-person game. The basic concept of bargaining is illustrated in the example below. 

Amy wants a raise. Her demand is $40 per hour. She is about to discuss the matter with her employer, who can be in one of three states.
1) the employee values Amy < $40
2) the employee values Amy = $40
3) the employee values Amy > $40

We inspect the last case. The employee values Amy > $40, say $75. The situation is divided into three parts
1) Any wage between $0 and $40, Amy will reject
2) Any wage above $75, the employer will reject 
3) The value between $40 to $75 will lead to a mutually acceptable deal. It is known as the bargaining range.

The bargaining problem looks at the various possibilities of mutually acceptable settlements and tries to theorize how a particular solution can be arrived at.  

John F. Nash, The Bargaining Problem, Econometrica, 18 (2), 1950, 155
Bargaining 101 (#1): Introduction: William Spaniel

Bargaining Theory Read More »

The Rendezvous Problem

The Rendezvous Problem is a logical dilemma originally formulated by  Steve Alpern in 1976. Two people are lost in a location with n rooms. How should they move around to find each other in minimum time?  

Obviously, they have no cell phone to communicate (it’s 1976). The n rooms are identical and unlabelled, and the travelling time between any two rooms is the same.  

If both stay still, they will never meet. If both move randomly, they may take longer to meet (the expected meeting time = n). If one of them stays and the other moves, the meeting time reduces to n/2, but there is no way to decide who to move and who remains still.  

Anderson and Weber proposed a probabilistic solution in which each person, after each step, either stays at her current location with probability p or moves randomly with probability 1-p until the two meet. They estimated p = 1/2 for n = 2 and p = 1/3 for n = 3. When n is large, p becomes 0.2475; the expected meeting time is ca. 0.8289n steps. 

Rendezvous problem: Wiki
The rendezvous problem on discrete locations: Anderson and Weber

The Rendezvous Problem Read More »

Muddy Children Puzzle

Amy and Bob are back from playing, and their mother notices mud on their foreheads. She says, “At least one of you has a muddy forehead. Do you know whether you have muddy foreheads?” What is the expected answer from each? What happens if she repeats the question? 

This is a puzzle in which each child can see the forehead of the other but not themselves. They must also answer simultaneously. 

Amy sees mud on Bob’s forehead, so she can’t conclude anything about herself. Had she seen no mud on Bob, she could deduce that she got muddy (as there is at least one). The same is true with Bob, who can’t decide. So they both say NO.  

When the mother asked again, the first NO became known to both children. Amy knows that Bob knows that Amy’s forehead has mud and vice versa. So both say YES this time.     

Induction Puzzles: Wiki

Muddy Children Puzzle Read More »

The First to Reach 15

Amy and Becky are playing a game. There are nine cards, numbered 1 to 9. The players take turns and pick up one card. The first player to pick up a set of three cards that add up to 15 wins the game. What is the strategy? 

The game’s objective is to create possible sets of 3 numbers that add up to 15. This can be achieved by building a 3 x 3 matrix as follows. 

So, Amy starts the game by picking one of the numbers, say 5. Let’s mark it by X. 

Becky then wants to complete a row or a diagonal, preventing Amy from doing so. She picks 6, denoted by O.

In other words, this game has become a tic-tac-toe, where a draw is also possible.

Game Theory Puzzle: The Race To 15: MindYourDecisions

The First to Reach 15 Read More »

Strictly and Weakly Dominant Strategies

After a brief break, we are back to the game theory topic. We know what a dominant strategy is. In a game, it is a player’s go-to strategy, regardless of what the other players do. The most famous example is the Prisoner’s dilemma, where Prisoner 1 has a dominant strategy – to betray—regardless of what Prisoner 2 does. There are two types of dominance. 

A strictly dominant strategy: Always provide the player with a greater (never equal to) payoff.

A weakly dominant strategy: Provide at least as good as the other strategies. At least one payoff is strictly greater.

In this game, from Player 1’s perspective, if Player 2 makes move 1, Player 1 gains a better payoff by making move 2 (7 > 5). On the other hand, if Player 2 makes move 2, Player 1 has no strictly better payoff (between move 1 and move 2). So, player 1 is good to make the move 2; however, it is a weakly dominant strategy.  

Strictly and Weakly Dominant Strategies Read More »

The 17 Coins Game

Another game Played between two players. In this case, 17 coins are placed in a circle. A player can take one or two coins in her turn. In the case of the two, they must be next to each other, i.e., there must be no gap between them. Whoever takes the last coin wins. Like before, the game offers an advantage to one person. Who is it, and what is her winning strategy?

Well, the advantage is with the second person. Here is the strategy: 

Case 1: the first person takes one coin

The second person must take two coins from the opposite side, breaking down the arc into two – with seven coins each. 

From now on, the game is simple: copy what the first person does on one of the arcs to the opposite arc. Since your turn is second, you will be the one who ends the game. 

Case 2: the first person takes two coins

The second person must also create two arcs with seven coins each by removing one from the diametrically opposite end. The rest is the same as before.  

Can You Take the Final Coin? A Game Theory Puzzle: William Spaniel

The 17 Coins Game Read More »