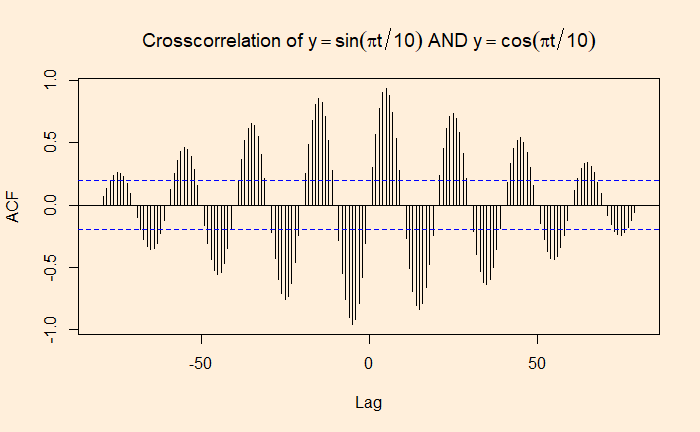
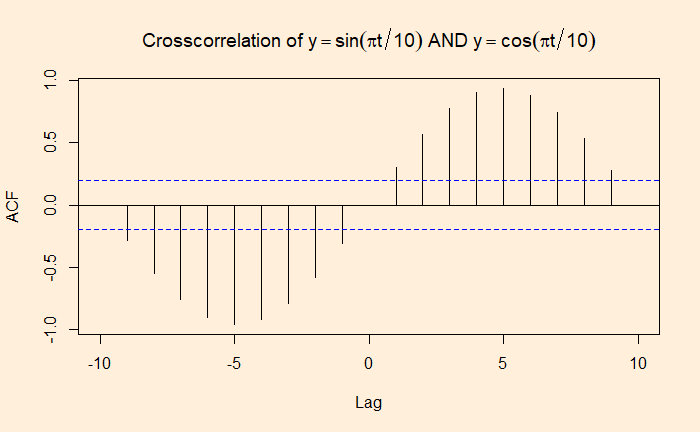
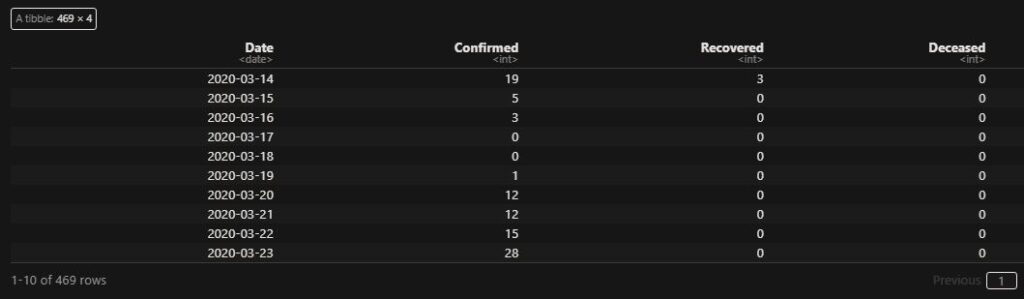
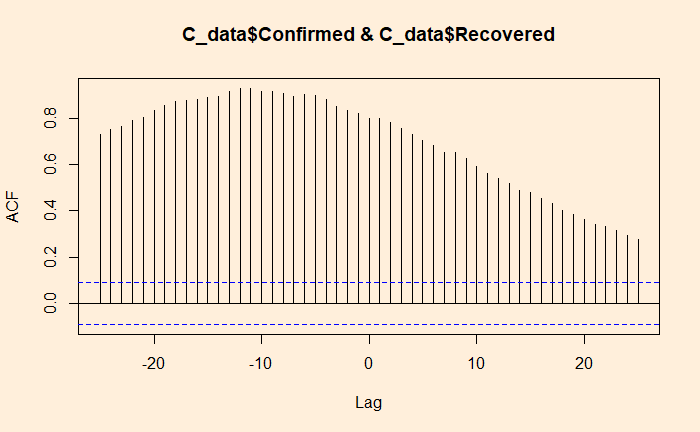
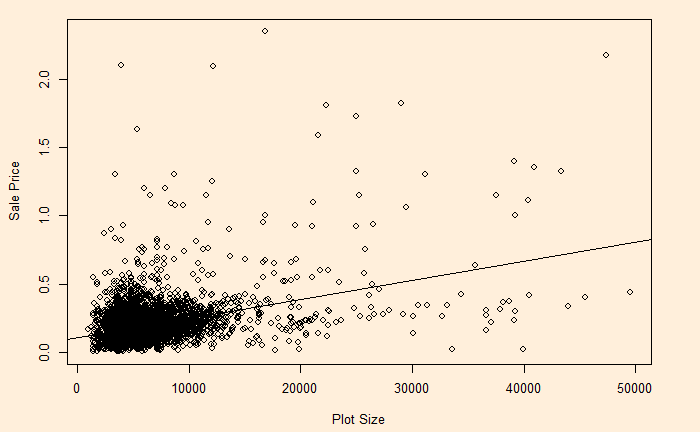
Identical Twins
1 in 10 sets of twins are identical, and 9 in 10 are fraternal. What is the probability that Adam and his twin brother Ben are identical twins?
Fraternal twins result from fertilising two eggs with two sperm during the same pregnancy. They may not be the same sex. On the other hand, identical twins result from the fertilisation of a single egg by a single sperm, with the fertilised egg then splitting into two. As a result, identical twins share the same genomes and are always of the same sex.
National Human Genome Reseach Institute
Contrary to how it appears otherwise, this is not a marginal probability but a conditional. The information that the twins are both males (Adam and his brother) triggers this shift. We will use the Bayes rule to solve this problem. The probability that Adam and Ben are identical twins, given they are males, is:
P(I|M) = P(M|I)xP(I)/[P(M|I)xP(I) + P(M|F)xP(F)]
P(M|I) = Probability of both males, given they are identical twins, is 1/2 (always same sex).
P(I) = Probability of twins being identical twins = 1/10
P(M|F) = Probability of both males, given they are fraternal twins, is 1/4 (MM out of the possible four, MM, FM, MF, FF)
P(F) = Probability of twins being fraternal twins = 9/10
P(I|M) = (1/2)x(1/10)/[(1/2)x(1/10) + (1/4)x(9/10)] = 1/5.5 = 0.1818 OR 18.18%
Reference
FRATERNAL TWINS: NIH
Counter-Intuitive Probability. What’s The Chance Twin Brothers Are Identical?: MindYourDecisions