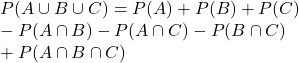February 2024

Dice Roll, Again

A pair of dice is thrown twice. What is the probability that the faces of the second throw are the same as the first?

Two types of outcomes are possible when you throw a pair of dice. In the first case, both dice show the same number (11, 22, 33, 44, 55, 66). In the second type, they differ (12, 13, etc.). We solve both scenarios separately.

Different

For a pair of dice, there are a total of 6 x 6 = 36 events possible. Of these, 6 are the same type (11, 22, 33, 44, 55, 66), and 36 – 6 = 30 are different. The probability of different numbers is 30/36.
When you repeat the throw, the exact two numbers come only in 2 out of the 36 outcomes. E.g., if 12 comes first, there are two ways of getting 12 in the second – 1 from the first die, 2 from the second OR 2 from the first or 1 from the second. The probability is 2/36.
The overall possibility of a repeat of pairs is (30/36)x(2/36)

Same

We have already seen that the probability of getting the same numbers in the first pair is 6 out of 36 (6/36). In the repeat, the situation only happens 1 in 36 (1/36).
The overall possibility of a repeat is (6/36)x(1/36)

We need to add the two probabilities to get the probability of getting the same in the repeat.

(30/36)x(2/36) + (6/36)x(1/36) = 0.0509; a 5% chance.

Dice Roll, Again Read More »

Principle of Inclusion-Exclusion – Applied

This time, we apply the inclusion-exclusion principle:
A fair die was rolled n times. What is the probability that at least 1 of the 6 values never appears?

The required probability is nothing but:
the probability of not getting a 1 OR
the probability of not getting a 2 OR
the probability of not getting a 3 OR
the probability of not getting a 4 OR
the probability of not getting a 5 OR
the probability of not getting a 6

P (A \cup B \cup C \cup D \cup E \cup F)

The probabilities are the same since it is a fair die (5/6).

Let’s apply the inclusion-exclusion principle:
1) Add all single probabilities: The probability of a given number missing in one roll = 5/6. All such single probabilities in n rolls = 6C1 x (5/6)n
2) Subtract all pair probabilities: The probability of the given two numbers missing in one roll = 4/6. All such pair probabilities = 6C2 x (4/6)n
3) Add all 3-tuple probabilities: The probability of the given three numbers missing in one roll = 3/6. All such pair probabilities = 6C3 x (3/6)n
4) Subtract all 4-tuple probabilities: The probability of the given four numbers missing in one roll = 2/6. All such pair probabilities = 6C4 x (2/6)n
5) Add all 5-tuple probabilities: The probability of the given five numbers missing in one roll = 1/6. All such pair probabilities = 6C5 x (1/6)n

6C1 x (5/6)n – 6C2 x (4/6)n + 6C3 x (3/6)n – 6C4 x (2/6)n + 6C5 x (1/6)n

For ten rolls, n = 10

n <- 10
choose(6,1) * (5/6)^n - choose(6,2) * (4/6)^n  +  choose(6, 3)* (3/6)^n - choose(6,4)*(2/6)^n + choose(6,5) * (1/6)^n
0.728

Similarly, for 20 rolls, there is a 0.15 chance of not getting at least one number.

Principle of Inclusion-Exclusion – Applied Read More »

Principle of Inclusion-Exclusion

We have seen the addition rule (OR Rule) of probabilities. It says
P (A OR B) = P(A) + P(B) – P (A AND B)

P (A \cup B) = P(A) + P(B) - P (A \cap B)

The above equation is a special case of the Principle of Inclusion-Exclusion (PIE). For the union of three events that are not necessarily disjoint:

\\ P (A \cup B \cup C) = P(A) + P(B) + P(C) \\ - P (A \cap B) - P (A \cap C)- P (B \cap C) \\ + P (A \cap B \cap C)

It goes by the sequence of adding and subtracting combinations of interactions.

P(A OR B OR C) =
Add all individual probabilities
subtract all pairs of probabilities (AND rule)
add all triplets of probabilities (AND rule), etc.

Let’s do an example to illustrate.

Principle of Inclusion-Exclusion Read More »

Poissonous Rain Drops

Raindrops are falling at a rate of 20 drops per inch per minute. What is the probability that no drop falls inside a 5-inch area for 3 seconds?

Since we consider the raindrops fall at random, we model this as a Poisson process. We need two parameters to estimate the required Poisson probability.
1) average rate of success: lambda
2) number of successes: s

Since we must consider zero success (s = 0) in a 3-second interval on a 5-inch area, we convert the success rate on the 5-inch area in 3 seconds.
lambda = 20 drops per inch per minute
= 20 x 5 = 100 drops per 5-inch area per minute
= 100/20 (= 5) drops per 5-inch area per 3 seconds

\\ P(X = s) = \frac{e^{-\lambda}\lambda^s}{s!} \\ \\ P(X = 0) = \frac{e^{-5}5^0}{0!} = 0.0067

OR

dpois(0, 100/20)

Poissonous Rain Drops Read More »

Probability of a Norepeatword

If one must make a random Norepeatword from the 26 alphabets, what is the probability of picking a work with all 26 letters? A Norepeatword is an assemblage of any number of alphabets (1 to 26) such that no letter is repeated. Let’s do the problem step by step.

  1. Number of 26 letter words: there are 26! words possible from 26 letters.
  2. Number of k-letter words (k = 1 to 26): It has two parts: A) how many k-letter words are possible from 26 and B) how many rearrangements are possible for each.
    A) 26Ck collections can be made from 26 letters with k letters.
    B) For each collection, k! rearrangements are possible.
    Therefore, the number of k-letter Norepeatwords is 26Ck x k!, and the total is obtained by summing from k = 1 to k = 26.

\textrm{\# norepeatwords} = \sum\limits_{k = 1}^{26} _{26}C_k * k! = \sum\limits_{k = 1}^{26} \frac{26!}{k!(26-k)!} * k!

The required probability is:

\\ P = \frac{26!}{\sum\limits_{k = 1}^{26} \frac{26!}{k!(26-k)!} * k!} = \frac{26!}{\sum\limits_{k = 1}^{26} \frac{26!}{(26-k)!}} = \frac{1}{\frac{1}{25!} + \frac{1}{24!} + ... + \frac{1}{1!} + 1}

The denominator of the equation is the famous Taylor series expansion of ex for x = 1.
ex = 1 + x + x2/2! + …

So, P = 1/e

Probability of a Norepeatword Read More »

All Three Girls

A family has six children – three boys and three girls. What is the probability that three older children are all girls?

Let’s label the children 1, 2, and 3 as girls and 4, 5, and 6 as boys. The required probability is nothing but:
The permutations for 1, 2, and 3 come up in the first three (any order) / All permutations
3! x 3! / 6! = 6/(6 x 5 x 4) = 1/20 = 0.05

Let’s use brute force and perform an R simulation.

itr <- 1000000

girl <- replicate(itr, {
   birth <- sample(seq(1:6), size = 3, replace = FALSE, prob = rep(1/6, 6))
   all_girl <- c(1,2,3) 

    if(all(all_girl %in% birth) == TRUE){
       counter <- 1
   } else {
       counter <- 0
   }
   
})
mean(girl)
0.050108

All Three Girls Read More »

Flipping for Winners

Sixty-four teams are playing a knockout tournament, and you have to predict the winners of each game. You get 1 point for correctly predicting the first-round winners, 2 for the second, 4 for the third, 8 for the fourth, 16 for the semi-finals and 32 for the final. If you flip coins to choose the winners, what is the expected number of points for predicting all the matches?

Round 1

The expected value of an event is the probability of occurrence x the payout. For a first-round match, the probability of predicting a single winner is (1/2), and the payout is 1.
The expected value for a single first round match = (1/2) x 1 = 1/2
Since there are 32 matches, the total expected value = 32 x 1/2 = 16

Round 2

The probability of predicting a winner in the second round means you need to get two coin flips right (first round and second round). The probability is (1/2) x (1/2). The Payoff is 2. The expected value is (1/2) x (1/2) x 2 = 1/2. For all the 16 matches in this round, it is 16 x 1/2 = 8.

Round 3

The probability is (1/2) x (1/2) (1/2). The Payoff is 4. The expected value is (1/2) x (1/2) x (1/2) x 4 = 1/2. Total = 8 x 1/2 = 4.

The next 3 rounds

The expected values for the next three rounds are 4 x 1/2, 2 x 1/2, and 1/2, respectively.

Adding all values: 16 + 8 + 4 + 2 + 1 + 1/2 = 31.5.

Flipping for Winners Read More »

A Car at a Junction

The probability of a car passing a junction in a 20-minute window is 0.9. What is the chance that a car passes the crossroad in a 5-minute window?

Let’s divide the 20-minute duration into four intervals of 5 minutes each. Let p be the probability of a car passing the junction in 5 minutes. Then, the chance of no car in 5 minutes is (1-p). We know the probability of not finding a car for 20 minutes, the joint probability of four such events happening one after another, is 1 – 0.9 = 0.1. Since these four incidents are independent, you can multiply, i.e., it is (1-p)4.

0.1 = (1-p)4
1 – p = (0.1)(1/4)
p = 1 – (0.1)(1/4)= 1 – 0.56 = 0.44

A Car at a Junction Read More »

Stem and Leaf Plots

A stem and leaf plot is a table of values. The arrangement can give a picture of the distribution of values. Here is the leaf plot of 20 values using the following R command.

numbers <- c(19, 37, 5, 12, 15, 32, 27, 35, 23, 22, 28, 34, 31, 12, 48, 31, 31, 28, 43, 3)
stem(numbers)
  The decimal point is 1 digit(s) to the right of the |

  0 | 35
  1 | 2259
  2 | 23788
  3 | 1112457
  4 | 38

There are five stems, 0, 1, 2, 3, and 4, listed one over another. The column on the right contains the leaves arranged from left to right.

How to read:
Take the first stem, 0. There are two numbers on the right, 3 and 5. That means the set has values of 3 (03) and 5 (05).

Stem and Leaf Plots Read More »