A woman who has a family history of Duchenne muscular dystrophy (DMD) gets tested for the presence of disease using a test (creatine phosphokinase, CPK) that has a sensitivity of 67% and a specificity of 95%. It is known that her brother has the condition. What is the probability that she is a carrier of the condition, and further, what is the chance that her son will have the disease if she tests negative in the CPK?
The conditional probability of disease, given the negative test result. We will use Bayes’ theorem to estimate the probability.
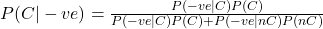
P(C|-ve) denotes the probability that she is a carrier (C), given she tested negative for the conditions (-ve).
P(-ve|C) is the chance of a negative result, given the person is a carrier. We know the chance of a +ve results if the person carries the gene. It is the sensitivity and is 67%. This means if the person carries a gene, there is a 67% chance of getting a positive and a 33% chance of getting a negative result. Therefore, P(-ve|C) = 0.33.
P(-ve|nC) is the chance of a negative result, given the person is NOT a carrier. It is nothing but specificity, and it is 95%. Therefore, P(-ve|nC) = 0.95.
This leaves the final two parameters: the prior probabilities that she carries or does not carry the disease genes (P(C) and P(nC)). DMD happens because of a mutated gene on the X chromosome. In our case, the woman can get that X chromosome from her father or mother. Since her brother had the conditions, and he could get X only from his mother, the mother is certainly a carrier of the mutated gene. Since the daughter inherited one of two Xs from her mother, P(C) = 0.5, which means P(nC) is 0.5.
Applying the Bayes’ theorem,
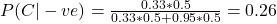
If she is a carrier (there is a 26% chance), she could pass one of her X chromosomes to her son at a 50% chance. This implies that the probability that her son gets the disease is 0.26 x 0.5 = 0.13 or 13%.
Reference
Bayesian Analysis and Risk Assessment in Genetic Counseling and Testing: Journal of Molecular Diagnostics, Vol. 6, No. 1, February 2004






