December 2023

Drunken Man Continues

The person in our previous two posts drinks every other day. As we have seen before, when he comes back, he must use the house key from the bunch of ten similar ones. As he can’t find which key is correct, he tries them individually when sober. When drunk, he pushes the same way but can’t distinguish which keys he has tried before.

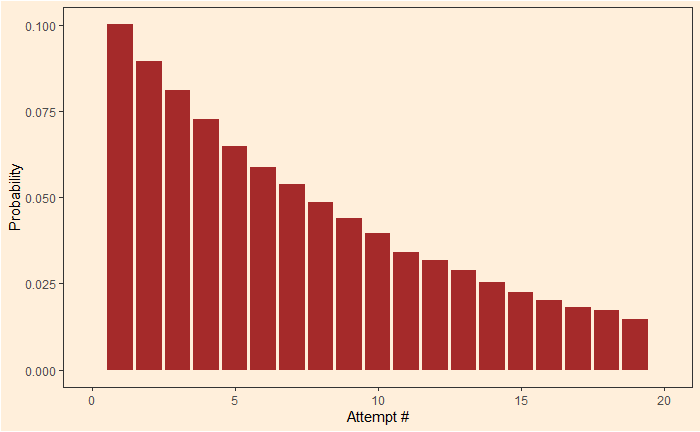
What is the probability that he was inebriated on the day he unlocked the door on his seventh attempt?

It is a conditional probability problem, and the ask is:
The probability that he is drunk, given he got the right key on the seventh attempt or P(D|7). We can use Bayes’ rule, that is,

P(D|7) = \frac{P(7|D)*P(D)}{P(7|D)*P(D) + P(7|S)*P(S)}

The terms are:
P(7|D) – Probability he opens on his 7th try, given he is drunk
P(D) – Prior probability that he is drunk on the day
P(7|S) – Probability he opens on his 7th try, given he is sobber
P(S) – Prior probability that he is sobber on the day

P(7|D) = (9/10)6 x (1/10) = 0.053
P(7|S) = (9/10)x(8/9)x(7/8)x(6/7)x(5/6)x(4/5)x(1/4) = 1/10 = 0.1
P(D) = 1/2
P(S) = 1/2

P(D|7) = \frac{0.053 * 0.5}{0.053 * 0.5 + 0.1 * 0.5} = 0.35

There is a 35% probability that he is drunk.

Drunken Man Continues Read More »

Drunken Man and the Room Key – Simulations

Here is the simulation of the problem of the drunken man and keys. Let me repeat the problem statement: A drunk man reaches his home and tries the door key from a bunch of 10 keys. If the first key doesn’t work, he returns the key to the bunch and randomly selects another key repeatedly until he opens the door. The question is: which precise trial has the highest probability of opening the door?

library(reshape)
library(ggplot2)

key <- 3
itr <- 100000

drunk <- replicate(itr, {
index <- 1
    for(i in 1:100) {
    sel <- sample(seq(1:10), 1, replace = TRUE, prob = rep(1/10,10))  
if(sel == key){
 index 
 break 
}else{
  index = index + 1
}
    }
index
    })

temp.melt <- melt(table(drunk))

ggplot(temp.melt, aes(x = drunk, y = value/itr)) +
  theme_bw() +
  geom_bar(stat = "identity", fill = "brown") +
  xlim(0,20) +
 
labs(x= "Attempt #",
       y= "Probability") +
  theme(legend.position="none") +

theme(text = element_text(color = "black"), 
        panel.background = element_rect(fill = "antiquewhite1"), 
        plot.background = element_rect(fill = "antiquewhite1"),
        panel.grid = element_blank())

Drunken Man and the Room Key – Simulations Read More »

Drunken Man and the Room Key

Here is an interesting but misleading probability question: A drunk man reaches his home and tries the door key from a bunch of 10 keys. If the first key doesn’t work, he returns the key to the bunch and randomly selects another key repeatedly until he opens the door. The question is: which precise trial has the highest probability of opening the door?

The question is misleading because it does not ask you to guess by which try the person will find the right key and open the door. We’ll come to that topic a little later. The task is to find the probability of finding the right key at each try and show which one is the highest.

The probability of finding the right key in his first attempt = 1/10; ten keys and finding one at random is one out of 10 possible options.
The probability of finding the right key in his second attempt = (9/10)x(1/10); it is the joint probability of not getting the right key in the first attempt (9/10) AND the chance of hitting the right on the second try.
The probability of finding the right key in his third attempt = (9/10)x(9/10)x(1/10). Here is the summary:

AttemptProbability
10.1
20.09
30.081
40.0729
50.06561

It doesn’t mean that person will open the door in the first attempt or never. We need to estimate something different to find how the probability of opening the door changes with attempts. The chance he opened the door in his second attempt is:
Probability he opened in the first OR probability he opened in the second = 1/10 + (9/10)*(1/10). Here is how that develops.

AttemptProbabilityProbability of
Right key by
Attempt
10.10.1
20.090.19
30.0810.27
40.07290.34
50.065610.41
60.0590.47

There is about a 50% chance he will open the door by his sixth attempt.

Drunken Man and the Room Key Read More »

Hide and Seek with Camouflage

Here is another hide-and-seek game but played with an inverse handicap. If the last case would have given a clue to the seeker 75% of the time, this time, it would help the hider 75% of the time on one location, i.e., the house. So the situation is

  1. There are two options to hide – behind bushes, behind the house.
  2. If the person hides behind the house, and the opponent searches the house, there is a 75% chance the seeker will not spot the hider (camouflage effective 75% of the time.
  3. If the person hides behind the bush, and the opponent searches it, it is normal, and no camouflage works.

We have seen similar puzzles before. Suppose there was no complication of camouflage; the players should mix their choices randomly at equal probabilities (0.5).

How should one search?

Let p be the probability that the seeker should search behind the house. The best value for p is such a way that the hider finds no particular incentive to choose one place over the other. In other words, the p makes the payoffs for the hider to hide behind bush and house equal.

Payoff to hide behind house = Payoff to hide behind bushes.
Pay off for hide behind house = p[1 x 0.75 + 0 x 0.25] + (1-p) x 1 = 0.75p + 1 – p
Pay off for hiding behind bushes = p x 1 + (1-p) x 0 = p

If the hider hides behind the house and the seeker searches the house, there is a 75% probability that she will gain one point and a 25% chance of zero. On the other hand, if the hider is behind the house and the seeker searches the bush, the hider gets a full score (one).

Solving for p,
0.75p + 1 – p = p
p = 0.8

How should one hide?

Let q be the probability that the hider must hide behind the house. Following the logic as before,

Payoff to search behind house = Payoff to search behind bushes.
Payoff to search behind house = q[0 x 0.75 + 1 x 0.25] + (1-q) x 0 = 0.25q
Payoff to search behind bushes = q x 0 + (1-q) x 1 = 1 – q

Solving for q,
0.25q = 1 – q
q = 0.8

Reference

Camouflaged Hide and Seek: William Spaniel

Hide and Seek with Camouflage Read More »

Hide and Seek Continued

We have seen a counterintuitive solution to the particular hide-and-seek game in which a signal (light) comes up at a fixed probability from one of the locations should one choose to hide there. Here is how one should hide, given the chance of the signal from the very location.

Let’s develop some intuition over the message from the plot. When there is no signal from one of the locations (the house), it becomes a normal hide-and-seek, and the person who hides must choose both places randomly at a 50:50 chance. On the other hand, when there is a signal from the house, the seeker can use it to her advantage, as some of the uncertainty over hiding behind the house gets eliminated by the presence of a signal and can search the other place more often. Once you understand the seeker’s mind, the hider must choose the house more often to counter the opponent.

The extreme case is when the probability of the signal is 99.99%, where the seeker can almost ignore the house and concentrate on the bushes. And that’s what the seeker will do, as seen in the plot below.

Hide and Seek Continued Read More »

Hide and Seek of the Second Order

Annie and Becky are playing hide and seek. Annie wants to hide, and it’s Becky’s job to find out. Annie has two choices – hide behind a house or the bushes. But there is a problem: if she hides behind the hose, there is a 75% probability that the surveillance system will catch her and a light will lit in the front. How often should Annie try to hide behind the house?

We have seen similar puzzles before. Suppose there was no complication due to light. In that case, intuition suggests that Annie and Becky should mix their choices randomly at equal probabilities.

Probabilities for searching

Becky’s strategy is designed to make both choices equally attractive to Annie. Let p be the probability that Becky search the house. Then, for Annie, the payoffs much match.

Hide behind house = Hide behind bushes.
Pay off for hide behind house = 0 x 0.75 + 0.25 [0 x p + 1 x (1-p)].
Pay off for hiding behind bushes = 1 x p + 0 x (1-p)

Explanation for the first equation. If Annie hides behind the house, there is a 75% probability that the light will lit and Becky will go and find her (or Annie ends up with 0). On the other hand, inside the 25% case, where no light is lit, there is a p chance Becky will go for the house and a (1-p) chance Becky will miss.

Solving for p,
0.25 – 0.25 p = p
p = 0.2

Probabilities for hiding

Let q be the probability for Annie to hide behind the house. Note that Becky will need to apply probabilities only when there is no light in front of the house. Annie’s strategy is to make payoffs for Becky equal (given no light).

The chance that Annie hides behind the house given no light is a conditional probability, and we must apply Bayes’ rule.

P(HH|NL) = P(NL|HH) x P(HH) / [ P(NL|HH) x P(HH) + P(NL|HB) x P(HB)]
= 0.25q /[0.25q + (1-q)]

Similarly, The probability Annie hides behind the bushes given no light is:
P(HB|NL) = P(NL|HB) x P(HB) / [P(NL|HB) x P(HB) + P(NL|HH) x P(HH)]
= (1-q) /[(1-q) + 0.25q]

Now, back to payoffs:

Payoff for Search house | no light = Payoff for Seach bushes | no light
Payoff for Search house | no light = 1 x [0.25q /[0.25q + (1-q)]] + 0 x (1-q) /[(1-q) + 0.25q]
Payoff for Search bushes | no light = 0 x [0.25q /[0.25q + (1-q)]] + 1 x (1-q) /[(1-q) + 0.25q]

0.25 q /[0.25q + (1-q)]] = (1-q) /[(1-q) + 0.25q]
0.25 q = (1-q)
q = 1/1.25 = 0.8

This is counterintuitive; Annie will hide behind the house 80% of the time, knowing the light will be lit 75% of those occasions.

Reference

Expert-Level Hide and Seek: William Spaniel

Hide and Seek of the Second Order Read More »

Banzhaf Power Index – Continued

The calculation of the Banzhaf Power Index is as follows.

  1. List all winning coalitions
  2. In each collision, identify the critical players
  3. Count how many times each player is critical
  4. Convert these counts to fractions by dividing them by how many times any player is critical.

Here are a few definitions before we go further:

  1. A coalition is a group of players voting the same way
  2. Winning coalition: If the total weight of the coalition is equal to or greater than the quota, it is a winning coalition.
  3. Critical player: If by leaving the coalition, a player in a coalition makes a winning coalition into a losing one.

All coalitions

Following are all the three-player combinations

PP <- c(15, 25, 10, 30, 20)

PP_Comb <- combinations(n = 5, r = 3, v = PP, set = FALSE)
P2_Comb <- as.data.frame(PP_Comb) 
P2_Comb$Sum <- rowSums(PP_Comb)
PlayerPlayerPlayerTotal WeightWinning
Coalition
15251050NO
15253070YES
15252060YES
15103055YES
15102045NO
15302065YES
25103065YES
25102055YES
25302075YES
10302060YES

All four-player combinations

PP <- c(15, 25, 10, 30, 20)

PP_Comb <- combinations(n = 5, r = 4, v = PP, set = FALSE)
P2_Comb <- as.data.frame(PP_Comb) 
P2_Comb$Sum <- rowSums(PP_Comb)
PlayerPlayerPlayerPlayerTotal WeightWinning
Coalition
1525103080YES
1525102070YES
1525302090YES
1510302075YES
2510302085YES

Finally, the 5-player combination: 15, 25, 10, 30, 20 = 100

The table of all the winning coalitions with critical players in bold follows.

P2,P4 (25,30)
P1, P2, P4 (15, 25, 30)
P1, P2, P5 (15, 25, 20)
P1, P3, P4 (15, 10, 30)
P1, P4, P5 (15, 30, 20)
P2, P3, P4 (25, 10, 30)
P2, P3, P5 (25, 10, 20)
P2, P4, P5 (25, 30, 20)
P3, P4, P5 (10, 30, 20)
P1, P2, P3, P4 (15, 25, 10, 30)
P1, P2, P3, P5 (15, 25, 10, 20)
P1, P2, P4, P5 (15, 25, 30, 20)
P1, P3, P4, P5 (15, 10, 30, 20)
P2, P3, P4, P5 (25, 10, 30, 20)
P1, P2, P3, P4, P5 (15, 25, 10, 30, 20)
PlayerCritical
Times 		Banzhaf
Power Index
P133/26
=11.5%
P277/26
= 26.9%
P322/26
= 7.7%
P499/26
= 42.3%
P555/26
= 19.2%
Total26

Player 4 has the highest voting power, with Banzhaf Power Index = 42.3%.

Banzhaf Power Index – Continued Read More »

Banzhaf Power Index

Let’s continue from the previous voting weights of five shareholders. This time, we calculate the power in the weighted voting system and determine the critical players. We use R functions to simplify the work. But first, the voting system:
[51: 15, 25, 10, 30, 20]
The shorthand notation indicates that 51% is required to reach the quota, and the players 1 to 5 have 15%, 25%, 10%, 30%, and 20% voting weights, respectively.

The calculation of the Banzhaf Power Index is as follows.

  1. List all winning coalitions
  2. In each collision, identify the critical players
  3. Count how many times each player is critical
  4. Convert these counts to fractions by dividing them by how many times any player is critical.

All coalitions

Following are all the two-player combinations

combinations(n = 5, r = 2, v = c("P1", "P2", "P3", "P4", "P5"))
      [,1] [,2]
 [1,] "P1" "P2"
 [2,] "P1" "P3"
 [3,] "P1" "P4"
 [4,] "P1" "P5"
 [5,] "P2" "P3"
 [6,] "P2" "P4"
 [7,] "P2" "P5"
 [8,] "P3" "P4"
 [9,] "P3" "P5"
[10,] "P4" "P5"

And their weights,

PP <- c(15, 25, 10, 30, 20)
PP_Comb <- combinations(n = 5, r = 2, v = PP, set = FALSE)
P2_Comb <- as.data.frame(PP_Comb) 
P2_Comb$Sum <- rowSums(PP_Comb)
PlayerPlayerTotal WeightWinning
Coalition
152540NO
151025NO
153045NO
152035NO
251035NO
253055NO
252045NO
103040NO
102030NO
302050NO

We’ll continue with the other player combinations in the next post.

Banzhaf Power Index Read More »

Weighted Voting

Weighted voting is a concept in which voters with different numbers of votes or influences determine the outcome of an election. The more votes someone holds, the more weight she gets in deciding the result. A simple example is a shareholder meeting where 51% of votes are required to settle a decision. Five shareholders hold 15%, 25%, 10%, 30%, and 20% of the total shares. Each of the shareholders gets a weightage corresponding to the shares they hold.

A: 15%
B: 25%
C: 10%
D: 30%
E: 20%
In the above example, Player D gets the highest weight, and Player C has the lowest. Quota is the minimum weight required to pass the election. And in our case, the quota is 51%.

If q represents the quota, w1, w2, etc., denotes the weight of player 1, player 2, etc., then the shorthand notation of the voting system is written as:
[q: w1, w2, w3, w4, w5]

In our example, it is
[51: 15, 25, 10, 30, 20]

Dictator: When one entity has a weight equal to or more than the quota. There is no dictator in [51: 15, 25, 10, 30, 20], but the third entity is a dictator in [51: 10, 20, 52, 18]. A dictator can pass or block any resolution, and nobody can win a vote without the dictator.

A player has veto power if her support is necessary to reach the quota. In [10: 6, 5, 4], player 2 and player 3 can only get the quota with support from player 1. Player 1 has veto power. On the other hand, player 2 or player 3 has no veto power. No one has veto power in [10, 6, 5, 7].

A player is a dummy if her vote is never essential for a group to reach quota. Player 3 is a dummy in [10: 7, 4, 2].

Weighted Voting Read More »

Airport Problem and the Shapley Solution

Here is how we apply the concept of Shapley Values to the famous airport problem.
Suppose an airport wants to build a runway to support three airline companies. Here are the requirements for each company:
Airline 1: 1500 m
Airline 2: 2200 m
Airline 3: 3000 m
Assume the cost per m of runway construction is $1k. How must the airport split costs among the three airline companies fairly?

Proportional rule

The simplest way is to split the cost proportional to the length each airliner needs, i.e., you divide the total cost proportional to the runway requirements as:

Airline 1: 3000 x 1500 / (1500 + 2200 + 3000 ) = 672k
Airline 2: 3000 x 2200 / (1500 + 2200 + 3000 ) = 985k
Airline 3: 3000 x 3000 / (1500 + 2200 + 3000 ) = 1343k

Is it a fair division? It seems so. But what happens if Airline 3 comes up with a variation, say, change to 3500? The new contributions get modified to:
Airline 1: 729k
Airline 2: 1069k
Airline 3: 1701k

Suddenly, this seems unfair for Airlines 1 and 2 as the new plan only benefits the third one, but the others also bear the extra costs (729 – 672) and (1069 – 985), respectively. So, we try the Shapley values:

Shapley value

We have seen how it works in the previous post. Let’s build the table first for case 1.

C(1500, 2200, 3000)

Combination 123
1231500700800
132150001500
23102200800
21302200800
312003000
321003000
Average3000/6
= 500		5100/6
= 850		9900/6
= 1650

And for case 2, C(1500, 2200, 3500):

Combination 123
12315007001300
132150002000
231022001300
213022001300
312003500
321003500
Average3000/6
= 500		5100/6
= 850		12900/6
= 2150

Case 1:
Shapley value Airline 1 = 500
Shapley value Airline 2 = 850
Shapley value Airline 3 = 1650

Case 2:
Shapley value Airline 1 = 500
Shapley value Airline 2 = 850
Shapley value Airline 3 = 2150

The game theory solution does not penalise the first two airlines and only demands the third one to pay for the scope change.

Airport Problem and the Shapley Solution Read More »