July 2023

Portfolio Theory

Portfolio theory is a simple theoretical framework for building investment mixes to achieve returns while managing risks. It used the concepts of expected values and standard deviations to communicate the philosophy.

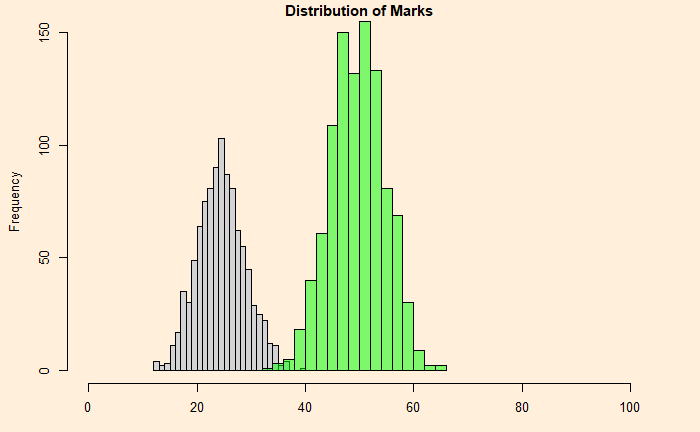
Take two funds, 1 and 2. 1 has an expected rate of return of 12%, and 2 has 6%. On the other hand, 1 is more volatile (standard deviation = 6), whereas 2 is less risky (standard deviation = 3), based on historical performances. In one scenario, you invest 50:50 in each.

The expected value is 0.5 x 12 + 0.5 x 6 = 9%

To estimate the risk of the portfolio, construct the following matrix.

Omega values (1 and 2) are the proportions, sigmas are the standard deviations, and sigma12 is the covariance between 1 and 2. Substituting 0.5 for each omega (50:50) and noting that covariance is the product of the standard deviations x correlation coefficient, we get the following table for the two securities that are weakly correlated (correlation coefficient = 0.5),

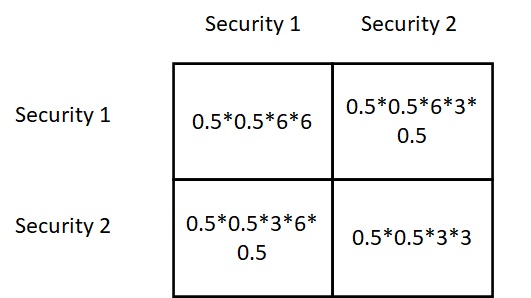
Add the entries in these boxes to get the portfolio variance. Take the square root for the standard deviation = 3.97.

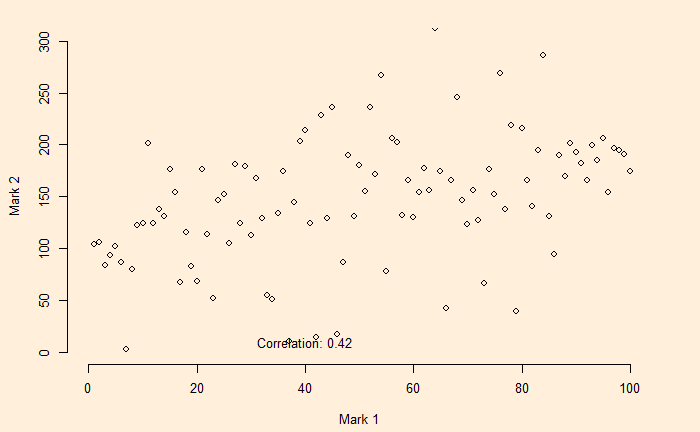
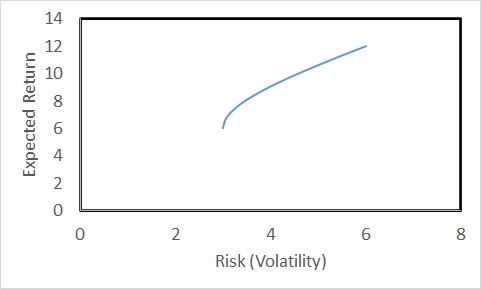
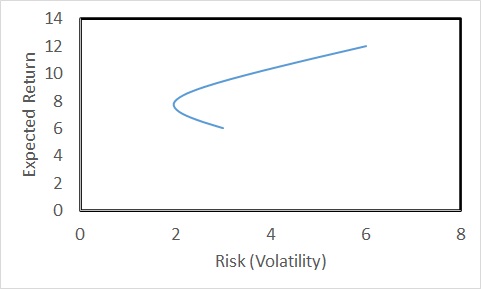
The expected rate of return of the portfolio is 9%, and the risk (volatility) is 3.97%. Continue this for all the proportions (omega1 = 1 to 0) and then plot the returns vs volatility; you get the following plot for a correlation coefficient of 0.5.

Imagine the securities do not correlate (coefficient = 0). The relationship changes to the following.

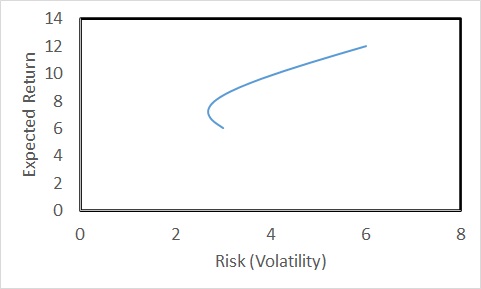
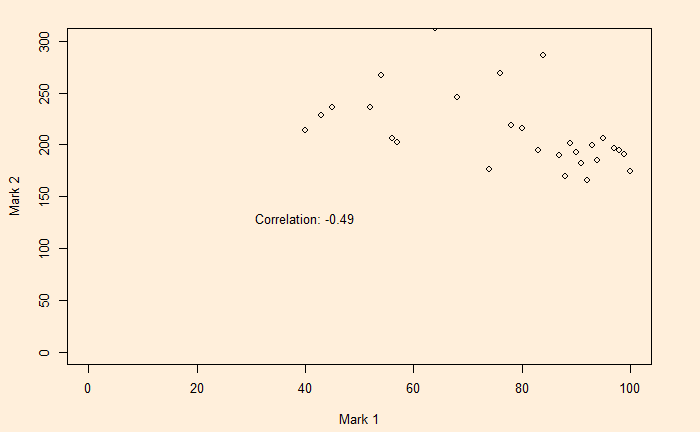
The risk is lower than the lowest (3%) for proportions of security1 less than 0.4. Even better, if the two securities are negatively correlated (correlation coefficient = -0.5),

If there are n securities in the portfolio, you must create an n x n matrix to determine the variance.

Portfolio Theory Read More »

Bayes’ Theorem – Graphical Representation

Here is a graphical illustration of Bayes’ theory. We use the old example of Steve, “the shy and withdrawn”.

The colour orange represents the number of librarians, and the light blue the farmers.

From the relative sizes of the rectangles, you make out that the number of farmers is more than the number of librarians. This, we call, the prior information.

Let’s assume that 80% of the librarians are shy and withdrawn, and only 25% of the farmers possess those characteristics. The following picture, green representing shyness, is more or less that.

Now, here is the question: when you see a random shy and withdrawn person, where do you likely to classify him, given you have two choices – librarian or farmer?

Well, likely in the rectangle on the left, which comes from the farmer group! And if you want a precise probability, here is the math below:

Bayes’ Theorem – Graphical Representation Read More »

The Net Present Value

Future Value

How much money will I have ONE year from today if I invest 100 dollars at an interest rate of 10%? Here, 10% is the annual return. The answer is 100 + 10% of 100 = 100 + 100 x 10% = 110. How much money will I have two years from now if I invest 100 dollars today at the same rate of return?

Value at the end of year 1 = 100 + 100 x 10% = 100 x (1 + 10%)
Value at the end of Year 2 = [100 x (1 + 10%)] + [100 x (1 + 10%)] x (1 + 10%) = 100 x (1 + 10%)2.
So, in general, the future value of P at the end of n years, at a rate of return of r, is:

FV = P x (1 + r)n

Present Value

Let’s ask the question in reverse. How much money should I invest to get 110 dollars in one year from today at a rate of return of 10%? We know that intuitively – it is 100. Formally, we get it by dividing 110 by (1 + 10%). By the way, 10% equals 0.1 (110/1.1 = 100). So the present value of 110 one year from now is 110 / (1 + 0.1). If we extend this further, the present value of C, n years from today, at a rate of return of r, is

PV = C/(1+r)n

Net Present Value

What is the present value (PV) of the future benefits that will happen in the following manner?

Year 1 = 200
Year 2 = 200
Year 3 = 200
Year 4 = 200

That must be PV of year 1 benefit + PV of year 2 benefit + PV of year 3 benefit + PV of year 4 benefit.

200/(1+0.1) + 200/(1+0.1)2 + 200/(1+0.1)3 + 200/(1+0.1)4 = 181.82 + 165.29 + 150.26 + 136.60 = 633.97.

The story is not over yet. What if I need to invest 500 dollars today to get the above benefits (200 dollars every year for 4 years)? Is it a good deal or a bad deal?

To get the answer, you estimate the present value of the future cash flows and subtract what is required to pay today. That is 633.97 – 500 = 133.97. Not bad. It is the net present value of this business.

The underlying principle behind these calculations is known as the ‘time value of money‘.

The Net Present Value Read More »

Simpson’s Paradox – Illustration

We have seen Simpson’s paradox multiple times before. Here is another illustration. Consider two countries; each has a million people. Following is the number of diseased individuals in a particular episode of the illness. So which country is safe to live?

Country ACountry B
# deaths
(per mln)		76.854.8

The conclusions seem pretty obvious,? Until you see the following breakdowns. First, the demographic distribution.

AgeAB
0 – 90.82
10 – 191.22
20 – 293.58
30 – 395.517
40 – 491119
50 – 591822
60 – 692119
70 – 79218
> 80183
Overall100100

And the incident rate of the disease

AgeAB
0 – 900
10 – 1901
20 – 2901
30 – 3912
40 – 491020
50 – 591030
60 – 6980100
70 – 79100200
> 80200300

Multiplying the respective columns gives the number of death per million people.

AgeAB
0 – 900
10 – 1900.02
20 – 2900.08
30 – 390.0550.34
40 – 491.13.8
50 – 591.86.6
60 – 6916.819
70 – 792116
> 80369
76.75554.84

The country that saved more people in each age category had more fatalities because it had more people in those buckets where the illness was severe.

Simpson’s Paradox – Illustration Read More »

School, Grades and the Collider

Another example of Berkson’s paradox, a collider bias, is the observed relationship, in surveys, between attending classes and grades. Here we illustrate the various possibilities and the results. Here, we explain the math using the following example.

AttendAttendDo Not
Attend		Do Not
Attend
Good
Grade		Poor
Grade		Good
Grade		Poor
Grade
300200200300

And this leads to the following conclusions:

  1. Probability of getting good grades, given the person attends classes, P(G|A) = # good grades and attend / total attend = 300/(300 + 200)= 0.6 
  2. Probability of getting poor grades, given the person attends, P(P|A) = 1 -P(G|A) = 0.4
  3. Probability of getting good grades, given the person doesn’t attend, P(G|N) = 200/(200 + 300) = 0.4
  4. Probability of getting good grades, given the person doesn’t attend, P(P|N) = 1 – P(G|N) = 0.6

Attending classes helps! But this information is never known outside. And it is where the survey gets interesting.

Imagine the survey captured the following proportions for each category.

AttendAttendDo Not
Attend		Do Not
Attend
Good
Grade		Poor
Grade		Good
Grade		Poor
Grade
0.90.50.50.1

Leading to the following Survey table.

AttendAttendDo Not
Attend		Do Not
Attend
Good
Grade		Poor
Grade		Good
Grade		Poor
Grade
27010010030

Now, calculate the probability tables, and compare with the actual.

SurveyActual
P(G|A)0.73
(270/370)		0.6
P(P|A)0.270.4
P(G|N)0.77
(100/130)		0.4
P(P|N)0.230.6

The survey tends to conclude the advantages of not attending classes!

School, Grades and the Collider Read More »

Berkson’s Paradox – Simulations

We have seen Berkson’s paradox before. It’s an erroneous correlation attributed to surveys done under specific conditions. Here we simulate a situation using R codes and illustrate the paradox.

Let’s assume a college admission process that involves two tests – test 1 and test 2. We create a set of random numbers with a positive correlation between Mark 1 and Mark 2.

x <- 1:100
y <- x + rnorm(100, 100,50)

plot(x,y, xlim = c(0,100), ylim = c(0,300),  frame.plot=FALSE, xlab = "Mark 1", ylab = "Mark 2")
text(paste("Correlation:", round(cor(x, y), 2)), x = 40, y = 10)

You will see that a reasonable positive correlation exists between the marks of the two tests (correlation coefficient = + 0.42).

Now, we impose a cut-off for the selection, i.e., the total marks (test 1 and test 2) of more than 250 to be eligible for admission.

plot(x,y, xlim = c(0,100), ylim = c(0,300),  frame.plot=FALSE,  col = ifelse(x + y > 250 ,'red','green'), xlab = "Mark 1", ylab = "Mark 2")
text(paste("Correlation:", round(cor(x, y), 2)), x = 40, y = 10)

And the eligible candidates are denoted by red circles.

Pick the red dots – the candidates who fulfilled the minimum criterion of total marks > 250 – separate and plot.

total <- data.frame(x = x, y = y, z = x+y) 
total <- total %>% filter(z > 250)

plot(total$x, total$y, xlab = "Mark 1", ylab = "Mark 2", xlim = c(0,100), ylim = c(0,300))
text(paste("Correlation:", round(cor(total$x, total$y), 2)), x = 40, y = 130)

If one surveys this college, there is a chance that the results find a negative correlation between performance in test 1 vs test 2 (in this case, a correlation of – 0.49). Imagine the first subject was science and the second was humanities! People might even attach causalities to the observations, which are biased by the selection criteria.

Berkson’s Paradox – Simulations Read More »

Skill, External Factors and Randomness

Think about it: a person attempts randomly to answer 100 multiple-choice questions – one correct answer out of four choices. What is the expected mark? Well, the first instinct could be 25. There are 100 questions, and the person who decides to attempt randomly has a one in four chance to get it right (1/4) x 100 = 25. Well, that’s an average, although, in reality, it follows a range.

Let’s run the following code to find out one such scenario.

itr <-1000

mark <- replicate(itr, {
sum(sample(c(1,0), 100, replace = TRUE, prob = c(1/4,3/4)))  
})

min(mark)
max(mark)

The output gives 12 and 40 (it will change once you repeat the calculation for randomness.

Now, we repeat the simulation with someone better at recognising the answer, i.e., a 50:50 chance of getting it right. Again, run 1000 individual runs and compare the distribution.

An extreme case is a comparison of the random with someone with 75% certainty about the answers.

Skill, External Factors and Randomness Read More »

Free Throws: What the Journalist Saw

It is a well-known fallacy to attach randomness with uniformity. And clusters are attributed to some reasoning. Here are 100 attempts on a basketball shooter who has 70% accuracy simulated.

bas_b <- sample(c(1, 0), 100, replace = TRUE, prob = c(7/10, 3/10))

You will see large clusters of successes (black dots) and a few clusters of emptiness. Overall, he is successful 70% of the time.

Imagine this happened over six games, and we show snapshots of four sub-sets of the plot as four different days of play.

Day 1 seems a very ordinary performance, followed by an excellent day 2.

Free Throws: What the Journalist Saw Read More »

Non-Ergodicity

Ergidicty is a concept in physics that equates the time average with the ensemble average of systems. In simple language, it means that the average property of a system remains the same by following one for several instances in time and averaging it (time average) or by averaging several states of the same at once (ensemble average). The first type is dynamic (changes with time), and the second is stochastic (statistical).

The assumption of ergodicity is fundamental to equilibrium statistical mechanics and, therefore, allows replacing dynamical descriptions with simpler probabilistic summaries. For example, the Brownian motion of gas molecules in a container is ergodic, meaning that a given molecule spends the same time in one half of the container as in the other half. In the coin tossing example, the average of results from tossing a fair coin infinite times equals tossing an infinite number of similar coins once.

Conversely, a stochastic process is non-ergodic when its statistics change with time. And this is what we saw in the special betting game.

Non-Ergodicity Read More »

Dunning–Kruger effect and Randomness

We have seen the Dunning-Kruger effect in the past. In his famous experiments, he collected data from 65 Cornell University graduates to verify what is known as the “above-average effect”. They made four predictions which formed the hypothesis that they wanted to test.

  1. Incompetent people overestimate their ability
  2. Incompetent individuals suffer from deficient meta-cognition abilities
  3. Incompetent people struggle with social comparison abilities
  4. Incompetent individuals can improve their insights by making them more competent

Signals and Noises

Nuhfer et al. used random number simulations to show plots of similar nature, suggesting issues with the study and the convention of using percentile plots. The graph convention holds ceiling effects wherein the lower quantile people overestimate their competency the most (more room available towards the top than the bottom). The top quantile (the competent participants) cannot overestimate by as much.

Dunning–Kruger effect and Randomness Read More »