We have seen information asymmetry. And it is a market failure. Why? Because it’s a feature that violates a fundamental theorem of welfare economics, i.e., “the competitive market will maximise the total social welfare”. In the event of a market failure, the overall group is worse off; we have seen one example in the past, i.e., externality.
Insurance is a good example of market failure due to information asymmetry. Another one is “the market for lemons,” which we’ll see in the end.
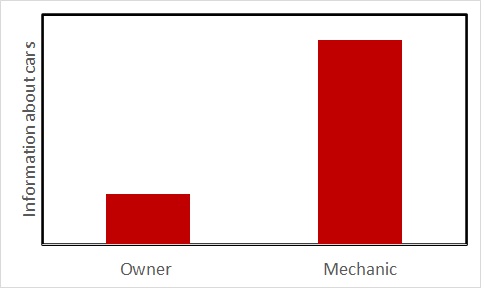
We saw the owner-mechanic case where the seller holds superior information. Insurance is a transaction where the opposite happens; the seller suffers from a lack of information about the (health condition) of the buyer. Suppose a target group of customers with 90% healthy and 10% sick. For the healthy, there is a 10% chance of incurring a $10,000 charge next year and the rest, none. For the unhealthy, there is a 50% chance of incurring $10,000 and 50% none. So, the expected values (of cost) are:
Healthy: 0.9 x 0 + 0.1 x 10,000 = 1000
Unhealthy: 0.5 x 0 + 0.5 x 10,000 = 5000
If everyone buys health insurance, the expected cost to the insurance company is:
0.9 x 1000 + 0.1 x 5000 = 1400.
Taking a profit of 100 per person, it sets a premium of $1500 for health insurance. Now, what happens in reality?
All the sick will buy the insurance, and only the risk-averse will buy from the healthy. Because the healthy will look at the expected cost (1000) and feel discouraged by the premium that costs 500 more. If there are a total of 1000 people, and 50% of the healthy are risk-averse (buyers of the insurance). Then, the revenue of the insurance company is
0.9 (proportion of healthy) x 0.5 (proportion of risk-averse) x 1000 (total people) x 1500 (premium) + 0.1 (proportion of unhealthy) x 1000 (total people) x 1500 (premium) = 0.9 x 0.5 x 1000 x 1500 + 0.1 x 1000 x 1500
825,000.
And the cost,
0.9 (proportion of healthy) x 0.5 (proportion of risk-averse) x 1000 (total people) x 1000 (expected cost on healthy) + 0.1 (proportion of unhealthy) x 1000 (total people) x 5000 (expected cost on unhealthy) = 0.9 x 0.5 x 1000 x 1000 + 0.1 x 1000 x 5000
950,000
The company loses money due to what is known as adverse selection. What happens if the company raises the premium? Well, it will discourage more healthy companies from entering the market, and the company will lose more money.
Market for Lemons
The problem of lemons is an example in the used-car market. Lemon is a poorly performing product. Since the buyer can’t tell the difference between a lemon and a good car (the plum), they are willing to pay some price corresponding to an average-performing car. Seeing what is happening, the top plum cars will exit the market, further compounding the miseries of the buyer (and the seller alike).
![]()