Bank Runs and Pareto Efficiency
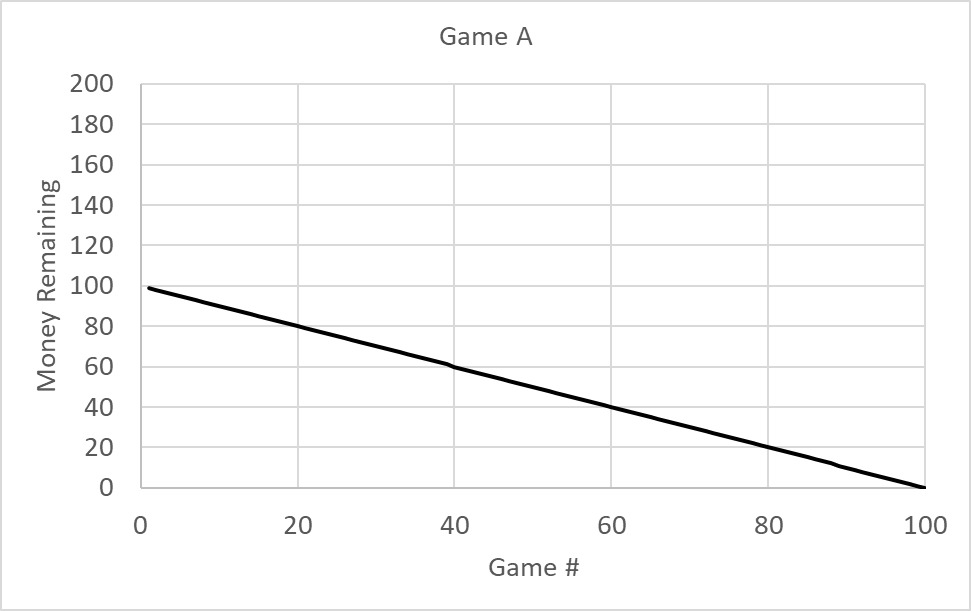
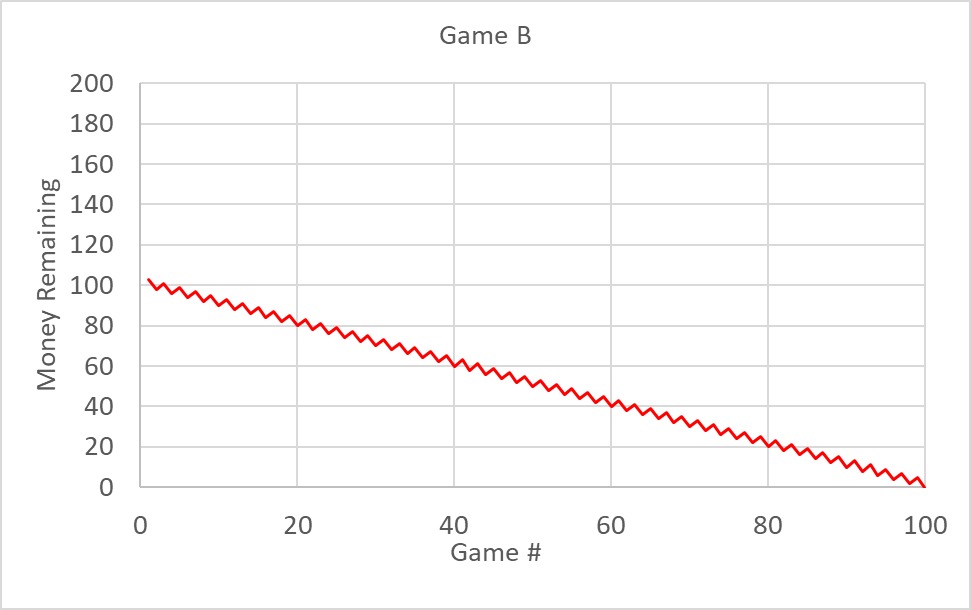
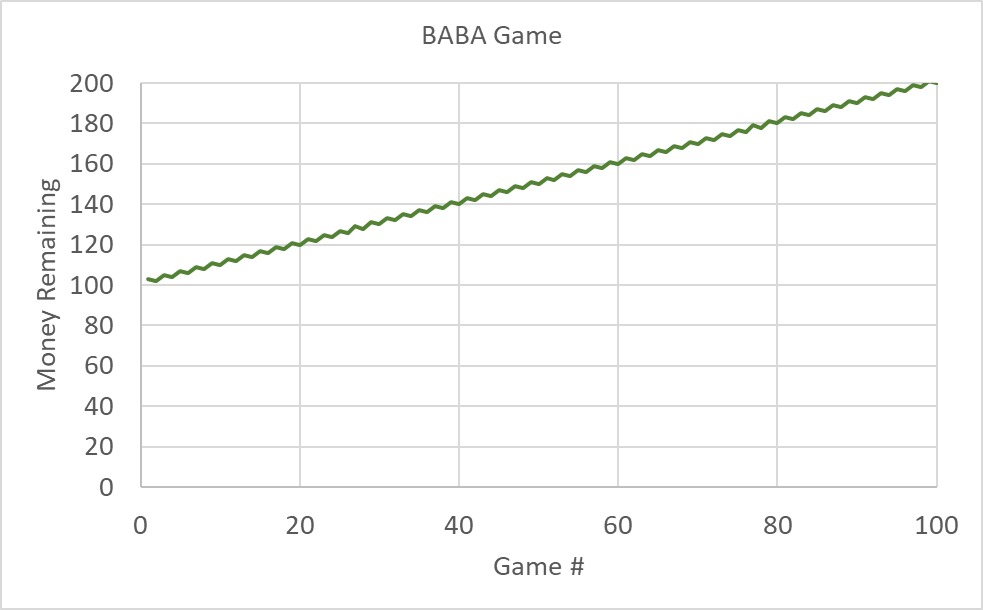
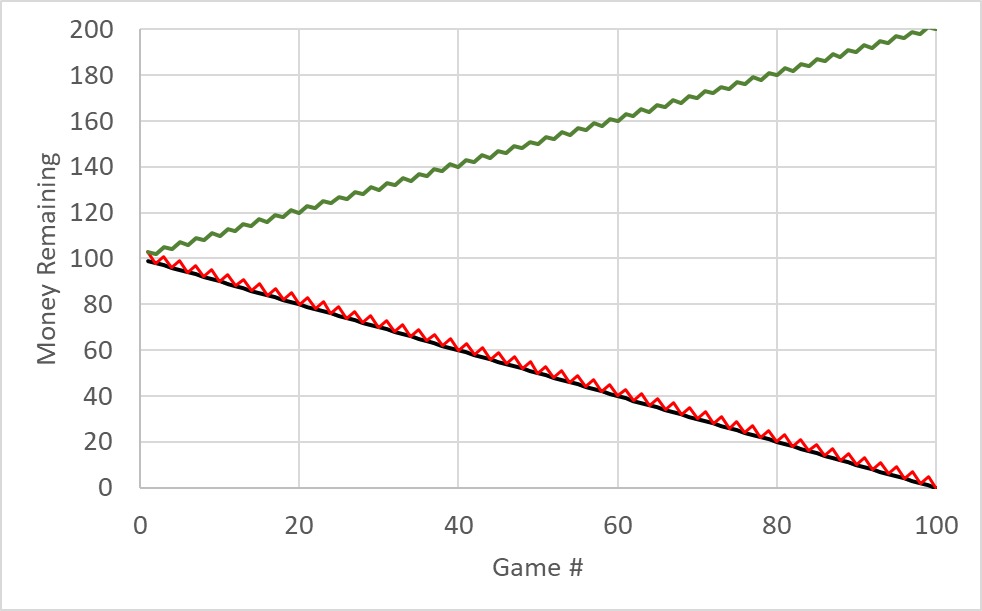
Let’s play a new game. Imagine there is a group of people. The players have two choices and payoffs: 1) Invest nothing and get nothing, 2) Invest $100, and there are there two outcomes: if more than 90% of the group invests, there is a net profit of $50, and if fewer than 90% invests, then the investor loses the money (-$100).
There are two Nash equilibria possible here. In the ‘good’ scenario, all invest and get profited. In the other case, no one invests; therefore, nobody loses. If the game is played for the first time, two things can happen: more than 90% invest and get a profit or fail to meet the 90% mark and lose money.
If the game is played many times, and if the players are rational, they will soon realise the basic mentality of the others and converge to one of the two outcomes – nobody invests, or everybody invests.
Bank runs and irrationality
A well-known case of such coordination failure is a bank run. As I write, we are on the cusp of a crisis at SVB (Silicon Valley Bank) in California, a significant start-up lender. So, why do bank runs happen? A bank run occurs when the depositors lose their confidence in the bank and start to withdraw their deposits. It is not a viable proposition as banks do not hold all the money in their vaults but lend or invest most of it to make a profit.
Rational customers with a good memory (of several previous incidents) may decide not to panic and stay invested. But what happens more often is people try to withdraw their money in the rush, only to pull the bank to a potentially avoidable, total failure.
Nash equilibrium: bad fashion and bank runs: YaleCourses
Bank Runs and Pareto Efficiency Read More »