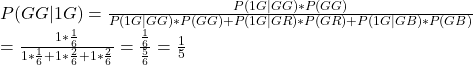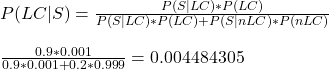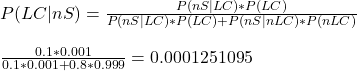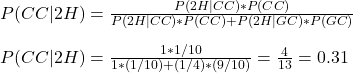Arrangement Problems
The distribution of objects into boxes is a classical statistics question, which I find very hard to understand. For example, the number of ways a person can distribute 36 chocolates among five kids in which nobody gets fewer than 5.
Let’s start with the concept of arrangements as permutations of objects and partitions. How many ways to distribute n balls into k boxes when the balls are distinguishable, and the order doesn’t matter? The following picture illustrates this question for n = 5 and k = 5.

From the picture, you may envisage the problem as the arrangement of 5 different (distinguishable) coloured balls and four similar (indistinguishable) partitions — a set up of 9 objects. If you get this concept clear, life becomes simpler.
The total possible arrangements are nothing but a distribution of n + k – 1 objects with k -1 items that are similar. Mathematically it is
(n + k – 1)!/(k – 1)!
Naturally, if the balls are indistinguishable, you will have to divide the term with n!

(n + k – 1)!/[(k – 1)! n!]
And if you notice carefully, it is a combination, i.e., (n + k – 1)C(k – 1)
Arrangement Problems Read More »