Lions and Wildebeests
Here is a puzzle I picked up from the internet: three lions and three wildebeests want to go from one side to the other side of a river. The river has a raft on which, at a time, up to two animals can travel. There is one problem, though. If the number of lions exceeds the number of wildebeest in one place, the lions would attack and kill the latter. So, how do they all reach the other side without issues?

Decision-making process
Let’s do a systematic decision tree that includes all (allowed) possibilities. What are the starting possibilities (trip 1)? They are one lion taking the raft (L), one wildebeest taking the raft (B), two lions (LL), two wildebeests (BB) or one lion and a wildebeest (LB). We will ignore L and B from the list because we know they must return (trip 2), thus nullifying trip 1. Therefore, the valid moves are:

An explanation for the shorthand: There are three options for trip 1 – LL, BB and LB. The notation in the parenthesis is the expected outcome in the end, e.g. if LL happens. And what remains on the start shore is LBB, and the endpoint (after the “/”) is LL. “X” means the move is unacceptable (three lions and one wildebeest on one side). The possible next actions (trip 2) are:

I guess the notations and the outcomes are clear by now. One of the trips (L) is not possible; it leads to 3 lions on one side. There are two possible remaining moves, and interestingly, both will lead to the same outcome (LLBBB/L). So, the next trip (trip 3) starts from a common origin (LLBBB/L).
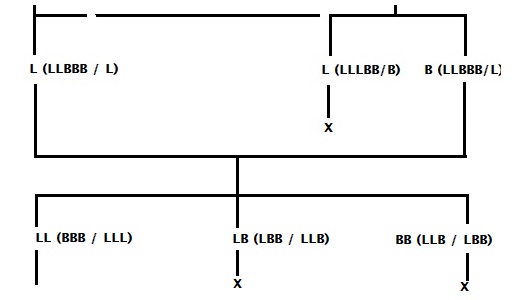
Trip 4:

Trip 5:

The following six trips are:

Can you solve the river crossing riddle? – Lisa Winer: TED-Ed
Lions and Wildebeests Read More »


