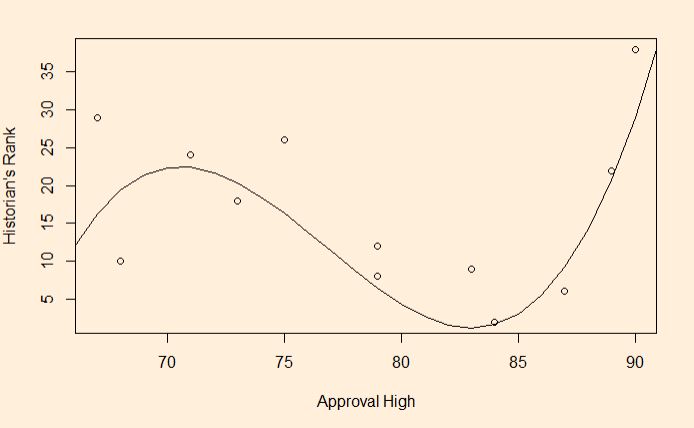
Double Poisson in the World Cup
Now that the top contenders of the double Poisson projection – Belgium and Brazil – are back home, even before the semi-final stage, it is time to reflect on what may have gone with the predictions.
Reason 1: Nothing wrong
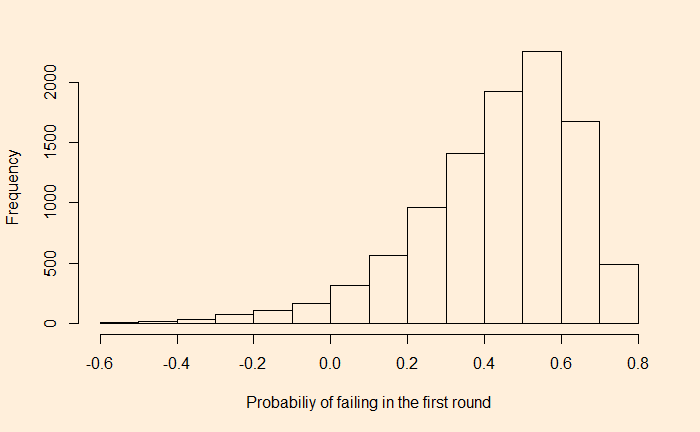
Nothing went wrong. The problem is with the understanding of the concept of probability. Having a chance of 14% may mean, in a frequentist’s interpretation, that if we play 100 world cups today, there could be about 14 times the Belgium team win. It also means around 86 times they don’t!
Reason 2: Insufficient data
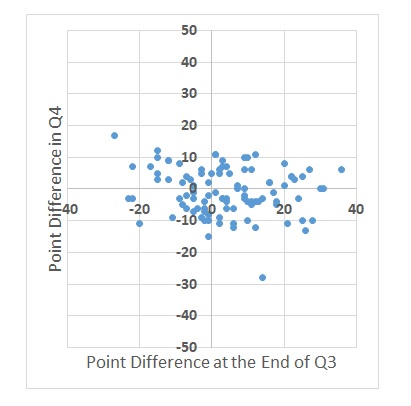
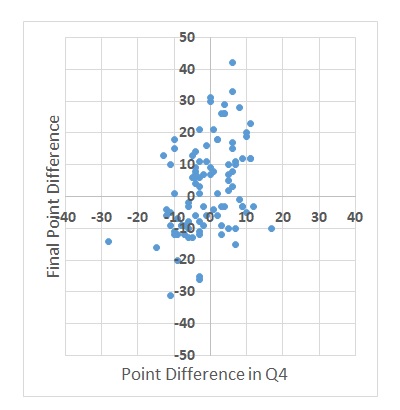
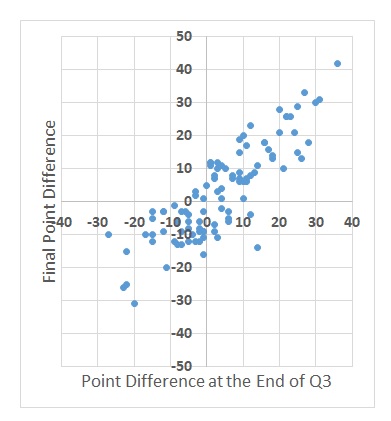
Insufficient data for the base model could be the second issue. As per the reference, the foundations of the model are based on two parameters, viz., attacking strength and defensive vulnerability. In a match between A and B, the former could be the historical average number of goals that team A had scored divided by the number of goals scored in the tournament. The latter could be the number of goals that team A has conceded.
Here is the first catch: if it was a national league of clubs or a regional (e.g. European) league of countries, getting a decent number of data between A and B is possible. In the present case, Belgium lost the chance because of the loss suffered by Morocco. Not sure how many serious matches these two countries played in recent years. In the absence of that data, the next best alternative is to calculate the same by team A against a team of comparable strength.
Reason 3: Time has changed
Especially true for Belgium, whose golden generation has been on the decline since the last world cup (2018). The analysis may have used data from the past, where they were really good, leading to the present, where they are just fine!
Reason 4: World cup’s no friendly
It again goes back to the quality of data. Regular (qualifying or friendly) matches can’t compare to a world cup match. Many of the strong contenders get back their final group of key players (from the clubs) only as the finals get closer. So, using the vast amount of data from less serious matches and applying them in serious world cup matches reduces the forecasting power.
Reference
How big data is transforming football: Nature
Double Poisson model for predicting football results: Plos One
Double Poisson in the World Cup Read More »