September 2022

Survival Plots – Kaplan-Meier Analysis

We will see how to make survival plots using the Kaplan-Meier (KM) method. The KM method is the cumulative probability of survival at regular intervals or whenever data is collected. Let’s go step by step to understand this. First, look at a data-collection table and familiarise yourself with a few terms.

The table describes the first few rows of 42 data points collected over 35 weeks (Data courtesy: reference 1). Week number represents the time, and the group describes if the person is treated with the drug or part of the control (placebo).

Week #GroupIllHealthy
6Treated31
7Treated10
9Treated01
10Treated11
11Treated01
13Treated10
16Treated10
1Control20
2Control20
3Control10
4Control20
5Control20

Time

In our case, it is the week number. We have a start of the study and an end of the study. Also, there are specific points in time for collecting data.

Event

The event, in this case, is the occurrence of illness.

Censoring

From the point of view of the study, there are people who have not yet experienced the event, i.e. remained healthy or were somehow left out of it at the time of data collection. These are people who are considered censored.

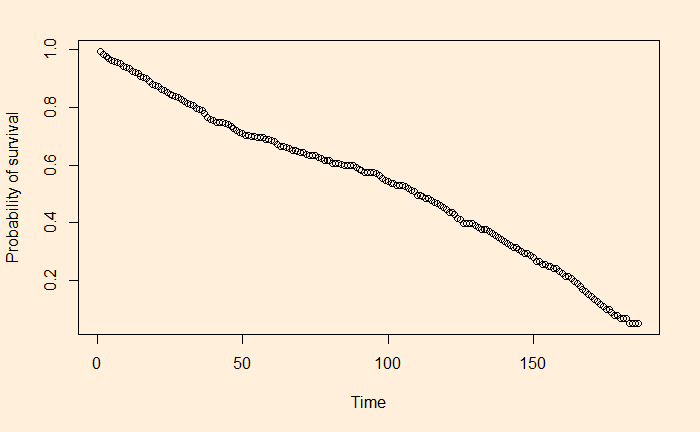
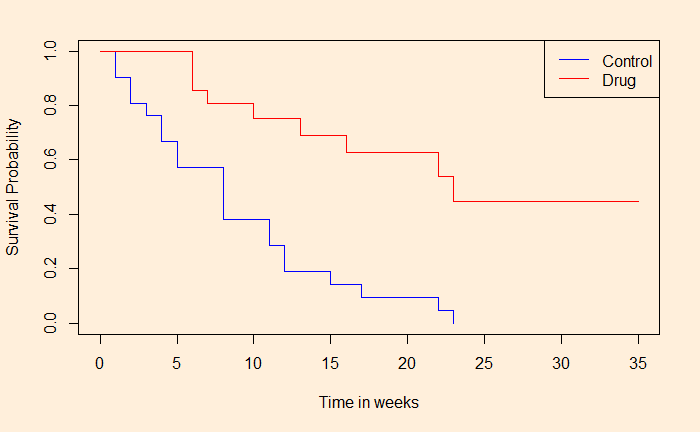
Survival plot

Here is the survival plot we obtained based on the Kaplan-Meier analysis. As you can see below, the graph shows the number of people who escaped the event (illness) at the end of the time frame. We’ll see how we got it using R next.

References

1) Generalized Linear Models: Germán Rodríguez
2) Kaplan–Meier estimator: Wiki
3) The Kaplan-Meier Method: karger

Survival Plots – Kaplan-Meier Analysis Read More »

Survival Plots

Survival analysis is used in many fields to understand certain events occurring as a function of time. Examples are patients surviving illness after treatments, employee turnover of companies, etc.

Survival plots are representations where the X-axis gives time, and the Y-axis gives the percentage (or proportion) of survivors or the portion that did not experience the event. Kaplan-Meier estimator is typically used to generate survival plots from experimental data.

Survival Plots Read More »

The Malaria Vaccine is Here

Malaria is one of the few mass-killer diseases still holding its fort against vaccines. It is because the culprits, parasites such as Plasmodium Falciparum, are more complex than viruses. But the story is changing. This week, The Lancet Infectious Diseases published an article summarising the study results of the R21/Matrix-M vaccine, which combines Oxford’s R21 and Novavax’s Matrix-M.

It was a randomised control trial involving around 400 children aged 5 – 17 months from Nanoro, Burkina Faso. The participants were divided into three groups to receive either a 25-microgram, 50-microgram malaria vaccine or a placebo. Note that 25 and 50 represent the doses of Matrix-M. R21 remained 5 micrograms in both cases. They also received a booster dose after 12 months. Note that the jabs were given before the malaria season.

Following was one set of results:

GroupPrimary Case
clinical malaria		Total
number
5 μg R21
25 μg Matrix-M		67132
5 μg R21
50 μg Matrix-M		54137
Control
rabies vaccine		121140

The numbers in the tables are the cumulative incident values collected over a year (from 14 days since the booster to 12 months). The Hazard Ratio (risk ratio of the intervention group to the control group) is estimated by regression of the survivorship plot using the Cox proportional hazards model. The efficacy = 1 – HR is estimated to be 71% for the low-dose group (group 1) and 80% for the high-dose group(group 2).

Efficacy and immunogenicity of R21/Matrix-M vaccine: The Lancet Infectious Diseases

Randomised Controlled Trials: BMJ

Types of malaria parasites: Stanford medicine

The Malaria Vaccine is Here Read More »

At Least One

How many times do we need to throw two dice to have a 50% chance of getting at least double-six? We have seen several of these “at least” problems. The magic of solving those problems is to find out the probability of no chance and then apply the AND rule (the joint probability).

The probability of rolling a double-six is (1/36), and that for no double-six is (35/36). It is because there are 36 total combinations possible once you roll two dice, and one of them is the desired.

Let n be the number of rolls for the desired outcome. The probability to have n events producing no double-six is (35/36)n, which is then equated to 0.5 for 50% probability. Solve the equation for n; (35/36)n = 0.5 or n ln(35/36) = ln(0.5). n = ln(0.5)/ln(35/36) = 24.5 ~ 25 rolls.

At Least One Read More »

The Aeroplane Boarding Problem – R Code

We have seen the aeroplane boarding problem in the previous post. Let’s try and verify that using an R program. Here is the code:

x_rand <- c(1,2,3,4,5,6,7)

f_seat <- sample(x_rand, size = 1)
x_rand <- x_rand[-f_seat]
print(paste0(" Firat one takes ", f_seat))
print(paste0(x_rand, " remains"))

for (i in 2:6){
  print(paste0("Next one is   ", i))
  if(i %in% x_rand){
    x_rand <- x_rand[-which(x_rand == i)]
     print(paste0(x_rand, " remains"))
  } else {
    n_seat <- sample(x_rand, size = 1) 
    x_rand <- x_rand[-which(x_rand == n_seat)]
    print(paste0(x_rand, " remains"))
  }
}
    print(paste0(x_rand, " Seat for Last"))
    if(x_rand == 7){
      counter = 1
    }else 
      counter = 0

And the output is:

[1] " Firat one takes 5"
[1] "1 remains" "2 remains" "3 remains" "4 remains" "6 remains" "7 remains"
[1] "Next one is   2"
[1] "1 remains" "3 remains" "4 remains" "6 remains" "7 remains"
[1] "Next one is   3"
[1] "1 remains" "4 remains" "6 remains" "7 remains"
[1] "Next one is   4"
[1] "1 remains" "6 remains" "7 remains"
[1] "Next one is   5"
[1] "1 remains" "6 remains"
[1] "Next one is   6"
[1] "1 remains"
[1] "1 Seat for Last"

Now, let us run the code for 100 passengers 10000 times and estimate the proportion for the last passenger to get the last seat.

success <- replicate(10000, {
  x_rand <- seq(1:100)

f_seat <- sample(x_rand, size = 1)
x_rand <- x_rand[-f_seat]

for (i in 2:99){
  
  if(i %in% x_rand){
    x_rand <- x_rand[-which(x_rand == i)]
  } else {

    n_seat <- sample(x_rand, size = 1) 
    x_rand <- x_rand[-which(x_rand == n_seat)]

  }
}
    if(x_rand == 100){
      counter = 1
    }else 
      counter = 0
})
   mean(success)

The answer is 0.5!

The proportion for the last passenger getting seat 1 is also 0.5. Try putting any other; the answer will be zero.

The Aeroplane Boarding Problem – R Code Read More »

The Aeroplane Boarding Problem

One hundred passengers are waiting to board an aircraft. The first passenger forgets her boarding pass and therefore takes a random seat. From here on, the passengers who follow take their own, if available, or take a seat randomly. When the 100th passenger arrives, what is the probability that she gets the right spot?

The answer is a surprising 1/2, and the only seats that remain for the 100th person are the seat of the first person or her correct one. Let’s run this exercise and prove the answer by induction.

Let the seat number of the first person who lost the pass be #37. When she comes inside, she has three possibilities to select (at random).

1) Select her seat, #37: In that case, everyone else, including 100th one, will board correctly.
2) Select the seat of the 100th person, say #13. Here, everyone else will sit correctly, and the last person has #37.
3) Select a random seat other than #37 or #13. She chooses #79.

All other passengers board properly until #79 arrives. She has three choices:

1) Take #37: This is the actual seat of the first passenger. If this happens, then onwards, everyone gets their respective.
2) Take #13. It is the last one’s seat. All others, except the last, get their assigned seat and #37 is available empty for the last one.
3) Take a random one from the remaining seats other than #37 or #13, only for the next unlucky one to repeat the game!

The Aeroplane Boarding Problem Read More »

The Optimal Stopping Strategy

Optimal stopping is a powerful rule in decision-making to maximise the reward. A famous example of strategy is the secretary problem or the fussy suitor problem.

The basic idea is the following. The person wants to choose the best one from a long list of candidates. She can get relevant data (e.g. through an interview process) from each prospect, one at a time. And she must decide to select or reject immediately after the interview. Although the ranking score remains available for reference, she can’t retake the rejected one.

The odds algorithm describes the solution to this problem and says that the probability of finding the optimal solution can be as high as (1/e ~ 37%) by following a methodology. e = 2.718, which is the base of the natural logarithm. The process is simple: if you have n candidates for the selection, give the candidates a score, reject the first n/e of them and then select the one whose score is greater than the greatest of the first n/e!

Let me explain. Imagine there are ten candidates (n = 10). Start the interview and score. Record the highest score of the first three (~ 10/2.718) but reject them all. Then, from the fourth candidate onwards, whoever gets a score more than the previous highest gets selected. The probability for the selected to be the best in the group of ten is about 37%.

We will look at the proof later, but let us run a Monte Carlo that verifies this idea using the following R code. Note this is not an algorithm to find the best, but one way of getting the chance of finding the highest number from a set of randomised numbers.

iter <- 100000

suitor <- replicate(iter, {
  high_number <- 100
  x <- 1:high_number
  x_rand <- sample(x)        

  min_num <- round(high_number/2.71)
  mmx <- max(x_rand[1:min_num])

  next_one <- min_num:high_number

  for (i in next_one){
      if(x_rand[i] > mmx){break}

}

   if(x_rand[i] == high_number){
   counter = 1
   }else{
   counter = 0
   }  
})

mean(suitor)

Here is the plot representing the probability as a function of the number of candidates.

The Optimal Stopping Strategy Read More »

Guessing the Card

Andy and Becky are playing a guessing game. Andy takes a card from a standard 52-card deck. Becky is to guess the card, but she can ask one of the three questions below.

1) Is it a card red?
2) Is the card a face card (J, Q or K)?
3) Is the card an ace of spades?

Which question should Becky ask to maximise the probability of the guess being correct?

Becky may ask any of the above as her winning chance remains the same.

1) Is it a card red?

There is a (1/2) chance of getting a yes answer from Andy. If the answer is yes, Becky can guess 1 of 26 red cards, and if the answer is no, she can guess 1 of 26 black cards.

2) Is the card a face card (J, Q or K)?

The probability of Andy answering yes is 12/52, and no is 40/52. If yes is the answer, Becky can guess the correct one with a probability of (1/12), and for no, it is (1/40). So the overall probability is (12/52) x (1/12) + (40/52) x (1/40) = (1/52)+(1/52) = 1/26.

3) Is the card an ace of spades?

For the last question, the probability of yes is (1/52) and no is (51/52). Correct guessing probability if yes is 1 and if no is (1/51). The overall probability is (1/52) x 1 + (51/52) x (1/51) = 1/26.

Guessing the Card Read More »

Two-Player Monty

In a different version of the Monty Hall problem, two players are playing the game; player one chooses a door and then player two another. If the car is behind the door that no one chose, Monty eliminates one of the players at random. If one has chosen the car, Monty eliminates the other player. The survivor knows that the other was eliminated, but not the reason. Should the survivor switch?

There are multiple ways of understanding this probability. One is to follow the three possibilities
1) Player 1 selects the car, and Monty will eliminate player 2. Switching is bad
2) Player 2 selects the car, and Monty will eliminate player 1. Switching is bad.
3) None picks the car, and Monty eliminates one at random. Switching is good.

It means switching makes sense only in the case when both players select goats. The chance of this happening is one in three; this is another way of saying there is a one-in-three chance of the car not being picked by anybody (three choices are: 1 picks the car, 2 picks the car, none picks).

So here is a Monty Hall problem in which sticking to the original door is the strategy.

Two-Player Monty Read More »

Three prisoners problem

Here is another one: Three prisoners are waiting to be executed in a few days. The authorities have selected one of them at random to be pardoned, and the warden knows who.

One of the prisoners, prisoner A, begs the warden to name one to be executed from the other two. Finally, the warden relents and says it is C. Prisoner A is happy now, thinking his probability of survival has increased from one-third to half. He then secretly tells the news to B. B is super happy, as he thinks his chance has doubled from one-third to two-thirds! Who is right here?

Remember the Monty Hall problem? This one is just another version of that. In other words, A’s chance of survival remained the same (1/3) even after the new information, whereas B’s chance doubled to two in three.

Three prisoners problem Read More »