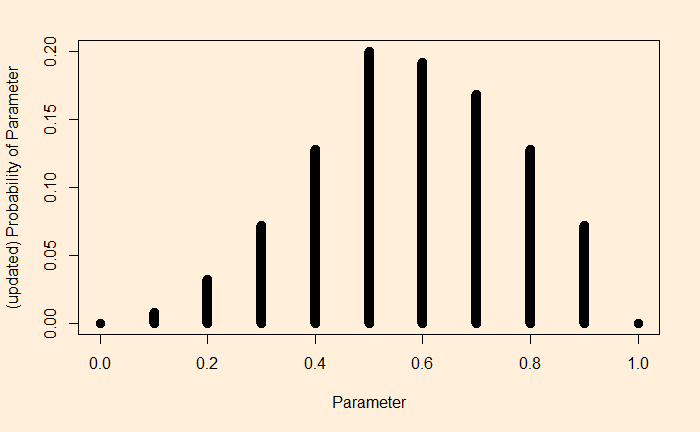
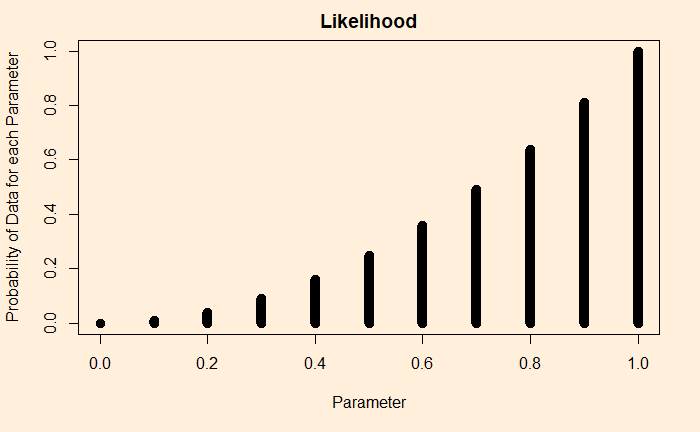
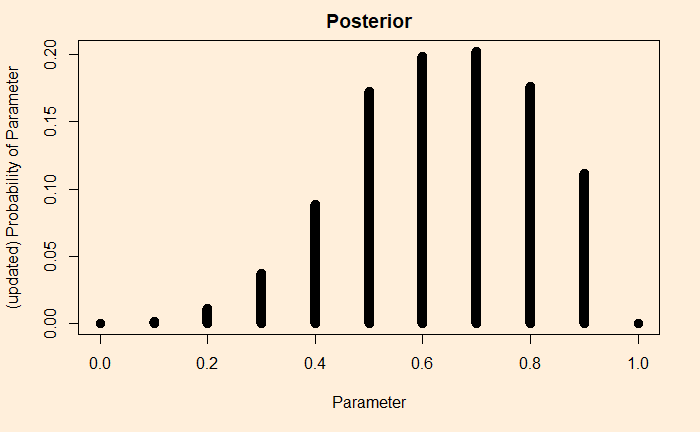
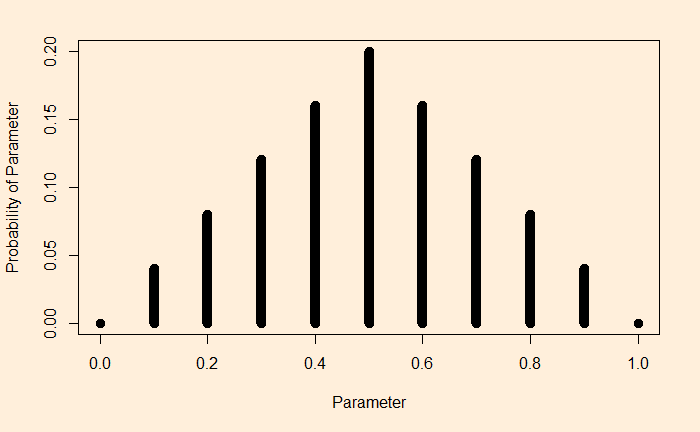
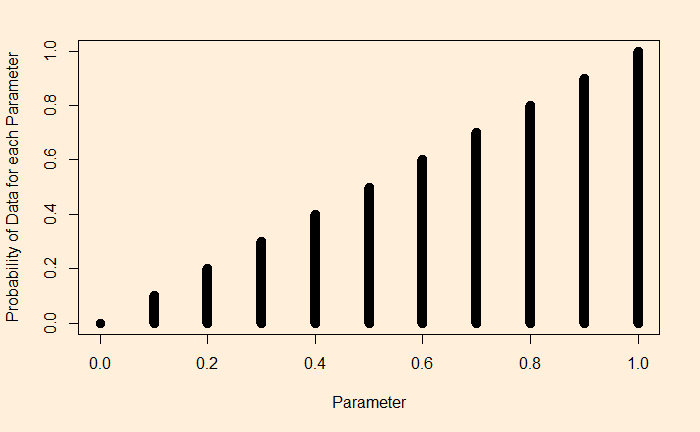
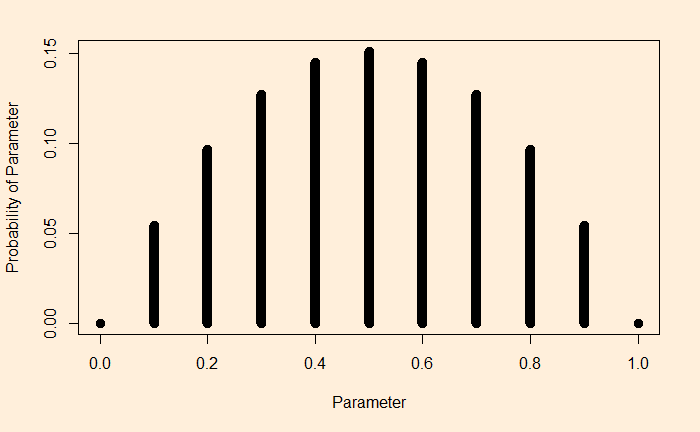
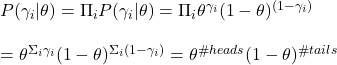August 2022

Bias in a Coin – Continued

A quick recap: in the previous post, we set a target of finding the bias of a coin by flipping it and collecting data. We have assumed a prior probability for the coin bias. Then established a likelihood for a coin that showed a head on a single flip.

We know we can multiply prior with the likelihood and then divide by the probability of the data.

P(\theta|D) = P(D|\theta) * P(\theta) / P(D)

The outcome (posterior) is below.

Look at the prior and then the posterior. You see how one outcome (heads on one flip) makes a noticeable shift to the right. It is no more equally distributed to the left and the right.

What would happen if, for the same prior, but getting two heads? First, calculate the likelihood:

You can see a clear difference here as the appearances of the two heads changed the likelihood heavily to the right. The same goes for the updated chance (the posterior).

Bias in a Coin – Continued Read More »

Bias in a Coin

Bayesian inference is a statistical technique to update the probability of a hypothesis using available data with the help of Bayes’ theorem. A long and complicated sentence! We will try to simplify this using an example – finding the bias of a coin.

Let’s first define a few terms. The bias of a coin is the chance of getting the required outcome; in our case, it’s the head. Therefore, for a fair coin, the bias = 0.5. So the objective of experiments is to toss coins and collect the outcomes (denoted by gamma). For simplicity, we give one for every head and zero for every tail.

\gamma = 1 \text{ for head and } \gamma = 0 \text{ for tail}

The next term is the parameter (theta). While the outcomes are only two – head or tail, their tendency to appear can reside on a range of parameters between zero and 1. As we have seen before, theta = 0.5 represents the state of the unbiased coin.

The objective of Bayesian inference is to estimate the parameter or the density distribution of the parameters using data and starting guesses. For example:

In this picture, you can see an assumed probability distribution of coins made from a factory. In a way, this is to say that the factory produces ranges of coins; we think the highest probability to be theta = 0.5, the perfect unbiased coin, although all sorts of other imperfections are possible (theta < 0.5 for tail-biased and theta > 0.5 for head-biased).

The model

It is the mathematical expression for the likelihood function for every possible parameter. For coin tosses, we know we can use the Bernoulli distribution.

P(\gamma|\theta) = \theta^\gamma (1-\theta)^{(1-\gamma)}

If you toss a number of coins, the probability of the set of outcomes becomes:

\\ P({\gamma_i}|\theta) = \Pi_i P(\gamma_i|\theta) = \Pi_i \theta^{\gamma_i} (1-\theta)^{(1-\gamma_i)} \\ \\ = \theta^{\Sigma_i\gamma_i} (1-\theta)^{\Sigma_i(1-\gamma_i)} = \theta^{\#heads} (1-\theta)^{\#tails}

Suppose we flip a coin and get heads. We substitute gamma = 1 for each of the theta values. A plot of this function for the following type appears:

Let’s spend some time understanding this plot. The plot says: if I have a theta = 1, that is a 100% head-biased coin, the likelihood of getting a head on a coin flip is 1. If it is 0.9, then 0.9 etc., until you reach a tail-biased one at theta = 0.

Imagine, I did two flips and got a head and a tail:

The interpretation is straightforward. To take the extreme left point: If it was a tail-biased coin (the parameter, theta = 0), the probability of getting one head and one tail is extremely low. Same for the extreme right (the head-biased).

Posterior from prior and likelihood

We have prior assumptions and the data. We are ready to use Bayes’ rule to get the posterior.

Bias in a Coin Read More »

Health Screening and Some Biases

This is not a post against health screening. In fact, I did my annual checkup yesterday, something I’ve been maintaining since my 30s. Today, we critically examine a few potential challenges associated with the much-advertised benefits of cancer screening.

Survival rates

The most common metric of reporting is the survival rate. It’s the percentage population who are diagnosed with an illness that survives a particular period. Based on the local system, these periods maybe five years, ten years etc.

A long-term (2019-2013) study of prostate cancer from a French administrative entity was reported by Bellier et al. The results show the following features. The incident rate remained almost flat at around 850 per 100,000 from 1991 to 2003 for people aged 75 and over. Then the rate started decreasing at an annual rate of 7%. For the men aged 60-74, 1991 to 2005 showed a steady increase followed by a decrease similar to the older age. Overall, the younger group (60-74) had a higher 8-year survival rate (as high as 95%).

Lead time bias

Illnesses such as cancers have a particular pre-clinical phase, the time lag between the onset of disease and the appearance of symptoms. A screening test can catch the disease at this stage. The longer the pre-clinical phase, the higher the likelihood of catching early by testing. This creates a lead time in comparison with the untested. Even if the ultimate year of death is the same, the lead time adds to the statistics giving a false impression of survival rates.

Overdiagnosis

Overdiagnosis is the detection of an illness that would not have resulted in symptoms and death. As the screening rate increases, followed by treatment of the positives, it becomes difficult to know how many of them benefitted from the treatment.

Confounding

Confounding also comes to complicate the analysis. In the last few decades, along with advancements in diagnostic techniques, cancer treatments have also improved significantly, leading to higher survival chances for the early and late-diagnosed population. It makes the separation of benefits of early diagnosis less apparent.

Health Screening and Some Biases Read More »

Hormonal contraception and thrombosis

Studies have found that the usage of hormonal contraceptives increases the chances of thrombosis by 300 to 500 per cent. Isn’t it worrying? Definitely, it is worrying, but what is the absolute risk here?

Breaking news of the 60s

The association between certain types of oral contraceptives (that contain estrogen and progestin) with thrombosis has been known since the 1960s. Naturally, it led to attention from the media and panic in society, eventually to reduced usage and increased pregnancies.

A case of bad science reporting?

Hopefully, you have recognised the main issue with this report (remember the posts about covid vaccines and colorectal cancer.). A paper published in 2011 reviewed this case of thrombosis with root causes and relative risks. Among them was the absolute risk or the incidence of thrombosis for adults. It is 1 -10 per 100,000 per year. With the use of this type of oral contraceptive, the risk increase to 5 – 50 in 100,000 per year, which is up to 0.05%. But what about mishaps due to actual pregnancies and abortions? 

Finally, just how big is a 100% increase of a risk? Well, that depends on the absolute risk on which it is based!

Hormonal Contraception and Thrombotic Risk: A Multidisciplinary Approach: PEDIATRICS, 127(2), 2011

Hormonal contraception and thrombosis Read More »

Salamander Reporposed!

Salamanders are fascinating creatures that have drawn plenty of spotlight from biologists due to their significant position in our evolutionary path. These are amphibians, and it was no coincidence that they drew attention, as a missing piece between creatures of water and that of land, from scientists in the 19th century, inspired by the recent theory of evolution.

In one such pursuit, what the famous zoologist and the Professor at the Museum of Natural History in Paris, Auguste Dumeril, found provides a live example of the wonders of repurposing animal functions.

In 1864, Dumeril received six salamanders from a lake in Mexico. They were large adults with feathery gills and aquatic body shapes characteristic of life in water. He kept them together and even had them produce fertilised eggs. The children that came out of the cage shocked the researcher; they showed little resemblance to their parents. No gills and aquatic tail; they appeared like the terrestrial variety.

It was found out much later that there are two pathways of development for the salamander larvae, according to the surrounding environment. The salamander in the aquatic habitat goes through the default pathway, but the one on land undergoes this metamorphosis. We now know the change gets triggered by the amount of thyroid hormone in the bloodstream that activates or kills some cells. Same gene, same creature but a change of environment yielding dramatic change in the appearance of the end product!

Reference

Some assembly required: Neil Shubin

Salamander Reporposed! Read More »

Common Sense Continued

The not-so-hidden secret is that biological innovations never come about during the great transition they are associated with.

Neil Shubin, Some Assembly Required

Another case of common sense is the theory of evolution.

Theorem of evolution

While it is no more topic of debate, thanks to millions of data collected in the last one hundred odd years, the concept of evolution has confused the generations since the day it was proposed.

Evolution of common sense

The first one was the remnants of Lamarckian thinking that essentially assumes that evolution is what an organism aspires and achieves, in its lifetime, to adapt to its environment. For example, a giraffe, in pursuit of high-lying leaves, stretches its neck so much that its child gets her neck a little longer than her mother, and it continues.

The other group is less dramatic with their approach, though commonsensical. Feather occurred to birds because it enabled the birds to fly, which helped them to survive in that environment. Similarly, lungs and limbs happened just about when the water-living creatures prepared to come out to the land.

More and more pieces of evidence proved that this understanding is wrong. The features such as the lungs or the wings were part of predecessor creatures ages before they transformed into their next level. For example, fishes of all species had swim bladders that enabled them to navigate different depths in the water. As genetic studies have later found, the genes responsible for these air sacs are the same that propelled the development of lungs. In other words, when the fish’s successor came to land, it just repurposed the swim bladder for breathing.

Inventions to products

A closer analogy is the example of green hydrogen as a vector of decarbonised energy. Hydrogen production through water electrolysis using renewable electricity such as solar PV is considered a commercial-ready option for a carbon-free energy future. To anybody who followed the history of science, electrolysis is by no means a new technology.

Alkaline water electrolysis technology is more than 120 years old. It has been serving the niche market of caustic and chlorine until now.

Similar story for solar PV. Bell Labs announced a solar battery in 1954 that could produce electricity whenever a thin slice of silicon was contacted by sunlight, being celebrated as a miracle device by the leading newspapers of that time. At the time of its invention, it was so expensive that Bell Labs calculated a cost of $1.5m to power one home using their technology!

But nothing happened for another 65 years!

Repurposing under societal pressure

This chemistry of evolution, where the ingredients were made in the distant past, but mixing happens only today, has confused people and led to creating two bands of commentators. The first group, the Vaclav Smil-type, develops some allergy to “high-tech worshippers” and claims whatever happens today was a result of the 1880s. The second group are mesmerised by the speed at which discoveries are happening right in front of their eyes. Both got carried away by the chemistry of evolution.

Common Sense Continued Read More »

Climate Change and Common Sense

To all the people in the northern hemisphere who are currently reeling under extreme heat waves: your assessment of global warming is correct, but not for the reasons you think you are seeing.

Common sense is a general intelligence that enables a person to manage concrete everyday situations. It is common sense to switch the power off before removing a bulb from its holder. Wearing a protective glove before touching the metal pot on the kitchen hob is another.

In a survey conducted in Australia between 2010-14, 22% of the respondents thought climate change was not happening. When specifically asked about what their opinions are based on, about 37% of them attributed to common sense. It might sound absurd that about 20% of the people who believed in human-induced climate change also attributed their belief to common sense. And the views of both parties are not surprising. Phenomena such as global warming are understood only through the laborious examination of scientific data from hundreds of sources through the lens of mathematical models. And there is nothing commonsensical about it!

The offspring of hindsight

It is a fact that some of the lessons learned from science can later become part of the common sense knowledge in everyday life. But trusting that the opposite is also true is dangerous. We have seen multiple examples of logical fallacies previously. Availability bias is one of them. For a climate sceptic, the last year’s winter might be the guiding principle, whereas, for a climate believer, it’s the heat wave of this summer. One can prove either of these as instances of random events, even when the number of hard facts on climate change is irrefutable.

Overdependence on experience

Common sense is primarily a manifestation of personal experience; science, on the other hand, is a rational, evidence-based approach that operates through the collaborative actions of hundreds of trained minds. While individual scientists are fallible mortals with cognitive biases and beliefs, the rigour of methodology – validation and falsification – known as the scientific method, by its community elevates science from those shortcomings.

Climate Change and Common Sense Read More »

Self-Estimated Intelligence

We have seen self-assessment bias before. Self-assessment of intelligence falls closer to this. Many studies have shown this bias affects men and women differently. And this led to the term MHFH or Male Hubris, Female Humility in cognitive psychology. Note that this exists despite countless studies which failed to find any difference in the levels of general intelligence between men and women.

Apart from these so-called Dunning–Kruger effects, cultural stereotypes play a role in this gender bias. For example, there are study results in which the participants rated their fathers as more intelligent than mothers. Asking parents about their children also resulted in similar impressions. You add teachers, media, or the society as a whole, to this mix; the disaster is complete.

Higher self-esteem is also seen as a contributing factor to higher self-estimations. And gender, as a sex or a personality trait, masculine vs feminine, has a role in this.

Self-Estimated Intelligence Read More »

Occupancy Problem

In a village of 2000 people, what is the chance of finding a day in the year which is not the birthday of someone? How do you solve this problem? The solution to this problem makes use of the Poisson approximation for r entities trying to occupy n empty cells.

When r and n are high so that lambda = n exp (-r/n) is bounded, the probability of m empty cells becomes the Poisson distribution function, p(m; lambda).

In or case, lambda = 365 x exp(-2000/365) = 1.52. The required probability may be obtained by subtracting the chance of seeing no empty day from one.

1 – dpois(0,1.52) = 0.78 or 78%

Occupancy Problem Read More »

The curse of the VAERS: The Post Hoc Fallacy

Today we explore the difference between ‘after’ and ‘from’! Because it concerns a famous fallacy called “Post Hoc Ergo Propter Hoc“. So what does this cool-sounding Latin phrase mean? As per Wikipedia, it means: “after this, therefore because of this”. It is the interpretation that something happens after an event to something from it. Take the example of the CDC’s Vaccine Adverse Event Reporting System (VAERS).

Adverse Event Reporting System

The Centers for Disease Control and Prevention of the United States uses VAERS as a system to monitor adverse events following vaccination. The data was meant for the medical researchers to find patterns and, thereby, potential impacts of vaccines on human health. Naturally, the system gets scores of events ranging from minor health effects to deaths. And a section of the crowd interprets and propagates these events due to vaccination. So, where is the fallacy here?

What happened in 2020

The number of people who died in the US due to heart disease in 2020 is 696,962, which is about 2000 per million population. The figure is 1800 for cancer, 500 for respiratory illness and 310 for diabetes. So, roughly 4610 per million per year due to these four types of diseases.

Thought experiment

Let’s divide 20 million Americans into two hypothetical groups of 10 million each. The first group took the vaccine over one month, and the second did not. What is the expected number of people from the unvaccinated group to die of the four causes mentioned previously? About 3840. But they do not report to the VAERS.

On the other hand, imagine a similar death rate to the vaccinated group. If 10% of those 3840 people report the incident in the system, it will make 384 reports or about 4600 in the whole year.

The first case will be forgotten as fate, whereas the second will be celebrated by the media as: “vaccine kills thousands”!

References

Diseases and Conditions: CDC

Vaccine Adverse Event Reporting System (VAERS): CDC

The curse of the VAERS: The Post Hoc Fallacy Read More »