July 2022

The last banana is a probability riddle by Leonardo Barichello that I found in a TedEd video. It is a thought experiment as follows:

Two players are playing a game by rolling two dice. If the higher number of the two is 1, 2, 3 or 4, player A wins, whereas if it is 5 or 6, player B wins. Who has a better chance of winning the game?

Let’s play a million times

The primary aim of this post is to develop an R code that generates a million such games and calculate how many times A and B win. We will then compare the results with the theoretical solution.

A die has six sides, and an unbiased one gives equal chances for each of its faces, numbered one to six. In other words, the probability of getting any of the numbers is one in six or (1/6). So, first, we need to create a die, roll it two times and get two random outcomes.

Random generator

The sample function in R can make random numbers from the given sample space at the specified probabilities.

sample(c(1,2,3,4,5,6), size = 2, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))

The code has four arguments: the first one, c(1, 2, 3, 4, 5, 6), is an array of all possible outcomes. The second is size, the number of times you want to choose. Here we gave two, corresponding to the two dice rolls. ‘replace is TRUE’ because you want to replace what came out in the first roll before the second roll. Finally, you provide probabilities of occurrence for each element in the sample space. There are six in total, and because it is a fair die, we give them equal chances (1/6). When I ran the code 5 times, the following is what I got.

[1] 1 6
[2] 1 4
[3] 2 3
[4] 4 6
[5] 2 6

If you recall the rules, player A wins two times (games 2 and 3), and player B wins three (games 1, 4 and 5). But, to get a reasonable certainty for the probability by counting the outcomes (the frequentist way), you need to play the game at least 1000 times! And we are going to automate that next.

Repeating the exercise

The replicate function can repeat an evaluation as many times as you specify. A simple example is.

replicate(3,"Thougthful")

can give an output

[1] "Thougthful" "Thougthful" "Thougthful"

Instead, if you want to give a chunk of calculations and repeat, you can use brackets like this:

jj <- replicate(3, {
          1
  })
jj

The output of the above expression is 1 1 1.

Back to bananas

repeat_game <- 1000000

win_perc_A <- replicate(repeat_game, {

   die_cast <- sample(c(1,2,3,4,5,6), size = 2, replace = TRUE, prob = c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6))
     if (max(die_cast) <= 4) {
     counter = 1
   } else {
     counter = 0
   }

}
)

mean(win_perc_A)

The code will repeat the sampling a pair of numbers, estimate the maximum (max function) of the duo and count if the maximum is less than or equal to 4 (by assigning 1 for the target and 0 otherwise) a million times. Finally, you either count the successes (of A) or calculate the mean; I went for the latter.

To end

The analytical solution is rather easy. The criterion for player A to win this game is if both rolls remain at four or below. The probability of the first roll remaining at four or below is (4/6). The same is for the second roll. Since the rolls are independent, you get the joint probability of two die rolls by multiplying the numbers. (4/6) x (4/6) = 16/36 = 0.4444.

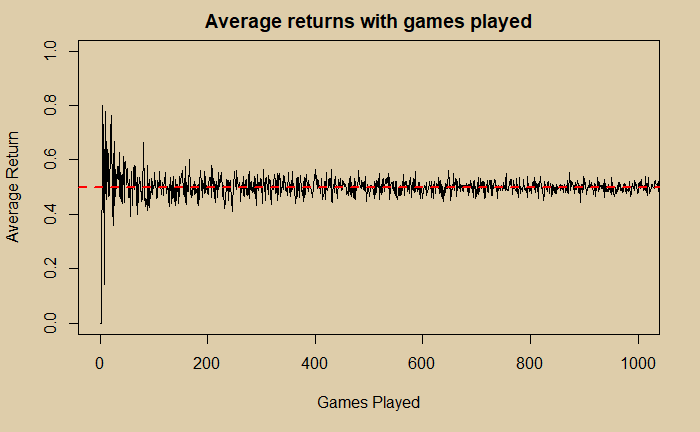
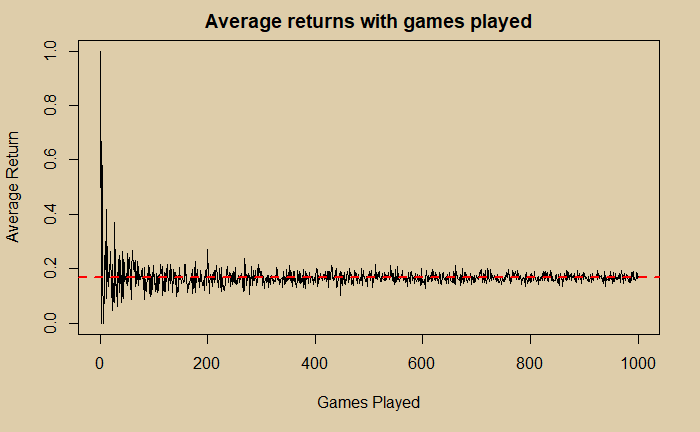
Now, what was the answer to the simulation? By taking an average of the counts of a million games, the answer was 0.444193. Not bad, eh?

So, the answer to the riddle? You better be player B in this game with about a 56% chance to win.

The last banana: A thought experiment in probability – Leonardo Barichello