February 2022

Regression to Mean and the Placement of Camera

What is an easy way to show that speed cameras reduce the number of accidents? Why are superstar children have a higher probability of not meeting their parent’s performance levels? Why do the popularities of movie-sequels dip compare to the originals?

There is a standard statistical phenomenon that connects the questions mentioned above. It is called regression to the mean. Regression is a process to establish a mathematical relationship between an observation and the variables that, we think, are responsible for the observation. In the mathematical language:

observation = deterministic model + residual error
By the way, the error does not mean a mistake but the sum of all random contributions (which was not explainable).

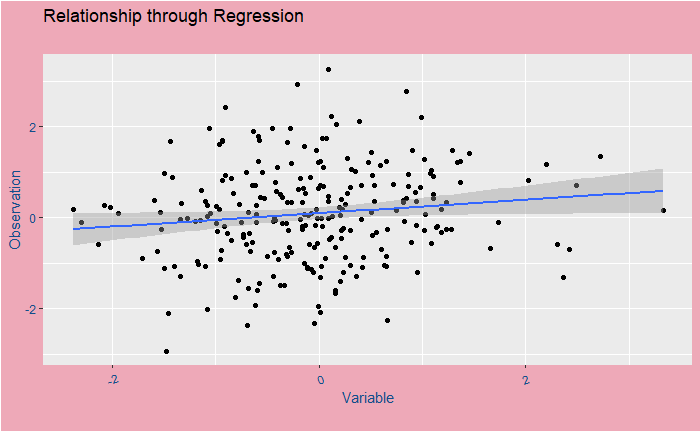
Regression to mean

The data points in the above plot represent a fictitious relationship between an observation and its variable. The blue line that passes through those points is the regression line or the best-fit line corresponding to a simple mathematical relation. In other words, following that line will tell you the expected value (mean) of the observation at any future value of the variable.

But the reality is the dots, all over the place but smoothly arranged around the line. Here is an important thing: if you see an observation above the line, the possibility for the next one to come below is high so that the average falls on the line. The opposite is true for an observation below the line.

Blockbusters and accidents

What is common to all those situations described in the beginning? One factor is that we selected extreme values, superstars, superhit moves. In other words, we tend to pick up only the points that are either lower or higher than the regression lines to draw comparisons. So, naturally, the next one (the children, luck, number of accidents, the height of people) has to come dramatically lower (if we talk about top events) or higher (if bottom events).

To end

The most suitable places to keep the speed cameras are the locations with the highest number of accidents because those are unlikely to retain their ranks even without cameras. Similarly, the likelihood of matching the pinnacle of success is small for the star personalities or the blockbuster movies considered for making a sequel.

Regression to Mean and the Placement of Camera Read More »

Expert’s Curse 3: Illusion of Objectivity

A study in 1977 ‘found’ that more than 90% of educators consider themselves above-average teachers. As per the study by Swedish psychologist Ola Svenson (1981), 88% of the Americans and 77% of the Swedes were in the ‘top half’ for driving safely. In another study conducted in 2017, experts agreed (71%) that cognitive bias is a concern in forensics, but only 26% thought that it affected their judgement!

The accounts mentioned above are examples of the illusion of objectivity. It arises from the belief that one understands the world better by their perceptions. You see a lot of it in politics, art and sports. Two prominent examples are the heavy influence of political partisanship in the actions of public policy experts and economics.

Expert sports analysts, especially those coming from the sports after retirement or those who regularly associate with the superstars, often lose their objectivity by being gravitated by the stardom. Remember those heated discussions between Steven A and Max Kellerman – the eternal tussle of adulation versus statistics?

[1] Patricia Cross, New Directions for Higher Education, 17, Spring 1977
[2] O. Svenson, Acta Psychologica 47 (1981) 143-148
[3] Kukucka et al., Journal of Applied Research in Memory and Cognition, 2017

Expert’s Curse 3: Illusion of Objectivity Read More »

Expert’s Curse 2: Intuition

Intuitive decision making, also known as naturalistic decision making (NDM), is often associated with experts. The scope of intuition ranges from the ultra-fast recollection of what was memorised before to simple gut feeling. It is essential, at this stage, to differentiate between intuition from heuristics (simple rules of thumb) and probabilistic estimation.

Firefighters and chess players are the favourite examples of the proponents of intuition. It is also a trait associated with people in creative fields. Grand master-level chess players can identify almost all the possible moves fast. Similarly, an experienced firefighter manoeuvres her actions effortlessly in times of crisis. A third example can be an F1 champion making an overtake and avoiding collision at 300 km/h speed! One thing common to all three experts is the number of hours they spend on practises. Let’s analyse these cases one by one.

A chess player or any other performing person, be in sports or arts, can not get help from a decision-making tool (e.g. a computer) during the act. So, irrespective of whether intuition is the best method or not, using the head remains the only option.

The firefighter does not have the time to perform a quantitative evaluation of each of the options she may have. Also, there is no guarantee that estimation is even possible in highly uncertain conditions. So they resort to recognising the patterns around them and applying the appropriate techniques from the hundreds they had encountered in their training and experience.

So intuition, that way, is restricted to those experts who have either no choice or no time. But for a doctor, a judge or a teacher, the situation is different. They have access to data, and support systems are available to collect and interpret more data. In such cases, more than their experience, the ability to avoid biases, acceptance of ignorance, and learner mindset are more valuable.

The final group include investment advisors, sports analysts and political commentators. They are experts who take pride in their experience and intuition. In reality, they work in fields filled with high levels of uncertainty, and, more often, their rates of success are no better than pure chances!

Daniel Kahneman and Gary Klein, “Conditions for intuitive expertise: a failure to disagree”, American Psychologist 64(6):515-26

Expert’s Curse 2: Intuition Read More »

Expert’s Curse 1: Base Rate Fallacy

The first one on the list is the base rate fallacy or base rate neglect. We have seen it before, and it is easier to understand the concept with the help of Bayes’ theorem.

P(H) in the above equation, the prior probability of my hypothesis on the event is the base rate. For the case study of doctors in the previous post, the problem starts when the patient presents a set of symptoms. Take the example of the case of UTI from the questionnaire:

Mr. Williams, a 65-year-old man, comes to the office for follow up of his osteoarthritis. He has noted foul-smelling urine and no pain or difficulty with urination. A urine dipstick shows trace blood. He has no particular preference for testing and wants your advice.

eAppendix 1.: Morgan DJ, Pineles L, Owczarzak, et al. Accuracy of Practitioner Estimates of Probability of Diagnosis Before and After Testing. Published online April 5, 2021. JAMA Internal Medicine. doi:10.1001/jamainternmed.2021.0269

The median estimate from the practitioners suggested that they guessed a one-in-four probability of UTI (ranging from 10% to 60%). In reality, based on historical data, such symptoms lead to less than one in a hundred!

Was it only the base rate?

I want to argue that the medical professionals made more than one error, i.e., base rate neglect. As evident from the answer to the last question, it could be a combination of two possible suspects—anchoring and the prosecutor’s fallacy. First, let’s look at the questions and answers.

A test to detect a disease for which prevalence is 1 out of 1000 has a sensitivity of 100% and specificity of 95%.

The median survey response was 95% post-test probability (in reality, 2%!) for a positive and 2% (in reality, 0) for a negative.

The prosecutor’s fallacy arises from the confusion between P(H|E) and P(E|H). In the present context, P(E|H), also called the sensitivity, was 100%, but the answers got anchored to 95% representing specificity. To understand what I just meant, look at the Bayes’ rule in a different form:

\\ \text{Chance of Disease after a +ve result} = \frac{Sensitivity * Prevalence}{Sensitivity * Prevalence + (1-Specificity)*(1- Prevalence)} \\ \\ \text{Chance of Disease after a -ve result} = \frac{(1- Sensitivity )* Prevalence}{(1- Sensitivity )* Prevalence + Specificity*(1 - Prevalence)}

So it is not a classical prosecutor’s case but more like getting hooked to 95%, irrespective of what it meant—it is more of a case of anchoring.

Expert’s Curse 1: Base Rate Fallacy Read More »

The Curse of Expertise 

Practitioners are experts. They could be medical practitioners, domain experts, lawyers and judges, leaders of organisations, sports persons-turned-pundits, to name a few. A lot of decision making rests on their shoulders, and the tool they often employ is experience. And experience is a double-edged sword! On the one hand, it makes them the most suitable people for the job, but on the other hand, they tend to ignore quantitative inference and rely on personal experience instead.

JAMA Internal Medicine collected responses from 723 practitioners from outpatient clinics in the US and published a paper in April 2021. The study aimed to estimate the understanding of risks and clinical decisions taken by medical practitioners. They included physicians and nurse practitioners. They were given a questionnaire to fill in the pretest and post-test probabilities of a set of illnesses. The requested post-test estimates included those after positive tests and negative tests.

The survey had five questions – four containing clinical scenarios (pneumonia, breast cancer, cardiac ischemia and UTI) and one hypothetical testing situation (a disease with 0.1% prevalence and test with 100% sensitivity and 95% specificity). The scientific evidence and the median responses are tabulated below:

Clinical
Scenario		Scientific
evidence 		Estimate
Resident
physician		Estimate
attending
physician		Estimate
Nurse
practitioner
Pneumonia
pretest
probability		25-42808580
post-test
after +ve test		46-65959595
post-test
after – ve test		10-19605050
breast cancer
pretest
probability		0.2 – 0.35210
post-test
after +ve test		3 – 9605060
post-test
after – ve test		< 0.055110
cardiac ischemia
pretest
probability		1-4.410515
post-test
after +ve test		2-11756090
post-test
after – ve test		0.43-2.55510
UTI
pretest
probability		0-1252030
post-test
after +ve test		0-8.377.59090
post-test
after – ve test		0-0.11555
Hypothetical
Scenario
post-test
after +ve test		2959595
post-test
after – ve test		0255

Those unheard are …

Before pointing fingers at the medical practitioners: you get this data because someone cared to measure, the specialists were happy to cooperate, and the Medical Association had the courage and insight to publish it. And the ultimate objective is quality improvement.

At the same time, the survey results suggest the lack of awareness of the element of probability in clinical practice and call for greater urgency to focus on scientific, evidence-based medical practice.

Morgan et al., JAMA Intern Med. 2021;181(6):747-755

The Curse of Expertise  Read More »

Hazard ratio and Chilli Magic

Clinical trials describe study results, which are essentially time-to-event data on risks, followed systematically from the standpoint of an event of interest, using the term Hazard Ratio (HR). HR gives the comparison of two risks positioned side by side on a survivorship plot. A survival plot can represent the number of people remaining alive in the study period, the time to disappear a pain, the time to recover from a disease in the presence of an intervention drug and so on.

Kaplan – Meier plot is a curve with time on the x-axis, and the proportion (or number) of people surviving is on the y-axis. For estimating the HR, the Kaplan – Meier plot should have two curves – one representing the intervention (experimental) group and the other the control (placebo) group.

Chilli pepper study

The famous 2019 paper on chilli pepper is an example to illustrate the hazard ratio. The researchers have followed a group of 22811 for about eight years and recorded the survival plot. The group had 15122 chilli eaters (experimental group) and 7689 non-chilli eaters (control group). A total of 1236 people had died by the end of the study, of which 500 were non-chilli eaters, and 736 were chilli takers. Let’s calculate:

Risk of death for chilli eaters = 736 / 15122
Risk of death for non chilli takers = 500 / 7689
The ratio = (736 / 15122) / (500 / 7689) = 0.75.
We will call the ratio the hazard ratio (HR) for the chilli eaters.

When the team looked at the specific cause of death, Cardiovascular disease (CVD), they found the following:

Risk of CVD mortality for chilli eaters = 251/ 15122
Risk of CVD mortality for non chilli takers = 193/ 7689
Hazard ratio = (251/ 15122) / (193/ 7689) = 0.66

So what are you waiting for? Eat your chilli and postpone the eventuality!

Bonaccio et al., Journal of the American College of Cardiology, 7 4 (25), 2019

Kaplan – Meier estimator: wiki

Hazard ratio and Chilli Magic Read More »

Risk ratio and Odds Ratio

What is the risk of you getting lost in the barrage of jargon used by statisticians? What are the odds of the earlier statement being true? Risks, odds and their corresponding ratios are terms used by statisticians to mesmerise non-statisticians.

Risk is probability, p

In medical studies, the phrase risk means probability. For example: if one person has cancer in a population of 1000 people, we call the risk of cancer in that society is (1/1000) or 0.001. For coin flipping, our favourite hobby, the risk of having a head is (1/2) = 0.5, and for rolling a dice, the risk of getting a 3 is (1/6) or 0.167. You may call it the absolute risk because you will see something soon that is not absolute (called relative), so be prepared.

Odds are p/(1-p)

Odds are the probability of an event occurring in a group divided by the probability of the event not occurring. Odds are the favourite for bettors. The odds of cancer in the earlier fictitious society are (1/1000)/(999/1000) =0.001. The number appears similar to the risk, which is only a coincidence due to the small value of the probability. For coin tossing, the odds of heads are (0.5/0.5) = 1, and for the dice, (0.167/0.833) = 0.2. Conversely, the odds of getting anything but a 3 in dice is (5/6)/(1/6) = 0.833/0.167 = 5.

Titanic survivors

SexDiedSurvivedRisk
Men13643671364/(1364+367)
0.79
Women126344126/(126 + 344)
0.27
SexDeathSurvivalOdds
Men0.791-0.790.79/(1-0.79)
3.76
Women0.271-0.270.27/(1-0.27)
0.37

The risk shuttles between 0 and 1; odds, on the other hand, it is 0 to infinity. When the risk moves above 0.5, the odds crosses 1.

Now, the ratios, RR and OR

Risk Ratio (RR) is the same as Relative Risk (RR). If the risk of cancer in one group is 0.002 and in another is 0.001, then RR = (0.002/0.001) = 2. The RR of losing dice rolling to coin tossing is (5/6)/(1/2)= 1.7. In the titanic example, the RR (between men and women) is (0.79/0.27) = 2.93.

The Odds Ratio (OR) is the ratio of odds. The odds ratio for titanic is (3.76/0.37) = 10.16.

Risk ratio and Odds Ratio Read More »

When Mother Became Nature

Sexual selection is a topic that invoked some controversy among evolutionary biologists. Darwin distinguished sexual selection as the difference in the ability to produce offspring, and natural selection, on the other hand, is about the struggles for existence.

Sexual selection is a combination of many factors. It could be a male-male struggle to reach a female, females snubbing males with certain features, or simply mating with certain males leading to weaker or no offspring.

mtDNA and NRY know it all

Whatever may be the precise reason, it has been established now using complex DNA analysis and computation that historically, more females and fewer males have participated in the development of the human race. In other words, throughout human history, leave the modern time when females started moving with their partners, fewer men participated in the reproduction process, although there are no reasons to believe that their respective numbers in the population were different. It went to such a low around 8000 years ago when the female-to-male effective population ratio was about 17!

References

Lippold et al. Investigative Genetics 2014, 5:13, Human paternal and maternal demographic histories: insights from high-resolution Y chromosome and mtDNA sequences

Genome Res. 2015 Apr; 25(4): 459–466, A recent bottleneck of Y chromosome diversity coincides with a global change in culture

When Mother Became Nature Read More »

What the Eyewitness saw

We have seen earlier that much of the evidence, depending on the nature, gives only moderate separation of the probability distributions of guilty and innocent curves. Evidence from the eyewitness is a leader that plays a pivotal role in the trial process. The pioneering work of Elizabeth Loftus reveals a lot about the fallibility of memory and the malleability of the brain by misinformation.

It’s in the wording

The first one is on people’s ability to estimate. In one experiment, the participants were asked to guess about the height of a basketball player. One group was asked: “how tall was the player” and the other, “how short was”. The ‘tall’ group estimated a higher number on an average than the ‘short’; the height difference between the tall to short was about 15 mm!

In the second experiment, 100 students were shown a video involving motor accidents and asked a few questions in which 6 were test questions – three of them about what happened in the movie and three that did not. Half of the subjects were given questions that were framed using ‘a’, such as Did you see a …? The other half were asked using ‘the’, such as Did you see the …? An overwhelmingly more number of people responded yes to the ‘the’ questions than the ‘a’ queries, irrespective of whether those events happened in the movie or not.

The role of presupposition

It is about asking one question followed by a second one. The purpose of the first question is to plant some seeds in the participant to influence the subsequent one. Forty undergraduates at the University of Washington were shown a 3-min video taken from the film “diary of a student revolution”. In the end, they were given a questionnaire with 19 filler questions and one key question. Half of the people got the question: “was the leader of the four demonstrators a male?” and the other half “was the leader of the twelve demonstrators a male?”. A week later, the subjects were back to answer 12 questions in which one key question was “how many demonstrators did you see in the movie”. The people who were asked “12” gave an average of 8.85 as the answer, whereas the “4” gave 6.4.

And the result?

The results make descriptions by witnesses one of the least reliable forms of evidence to separate guilty from the innocent. Do you remember the d’ of 0.8 from the earlier post?

Loftus, E. F., Cognitive Psychology 7, 560-572

Elizabeth Loftus: Wiki

What the Eyewitness saw Read More »

Justice and the Use of Prior Beliefs

The last two posts ended with rather pessimistic notes on the possibility of establishing justice under the complex world of overlapping pieces of evidence. We end the series with the last technique and check if that offers a better hope of overcoming some inherent issues of separating signals from noise using the beta parameter.

Beta comes from signal detection theory, and it is the ratio of likelihoods, i.e. P(xi|G)/P(xi|I). P(xi|G) is the probability of the evidence, given the person is guilty, and P(xi|I), if she is innocent.

Let us start from Bayes’ rule,

\\ P(G|x_i) = \frac{P(x_i|G)*P(G)}{P(x_i|G)*P(G) + P(x_i|I)*P(I)} \\ \\ P(I|x_i) = \frac{P(x_i|I)*P(I)}{P(x_i|I)*P(I) + P(x_i|G)*P(G)} \\ \\ \frac{P(G|x_i)}{P(I|x_i)} = \frac{P(x_i|G)*P(G)}{P(x_i|I)*P(I)} \text{or} \\ \\ \frac{P(G|x_i)*P(I)}{P(I|x_i)*P(G)} = \frac{P(x_i|G)}{P(x_i|I)} = \beta

So, beta depends on the posterior odds of guilt and the prior odds of innocent.

For a situation at a likelihood ratio of 1, if the prior belief, P(G), is lower, the jury is less likely to make a false alarm. Graphically, this means moving the vertical line to the right and achieving higher accuracy in preventing false alarms (at the expense of more misses).

The sad truth is that none of these techniques is helping to reduce the overall errors in judgement.

Do juries meet our expectations?: Arkes and Mellers

Justice and the Use of Prior Beliefs Read More »