What to Expect from Tossing of Coins
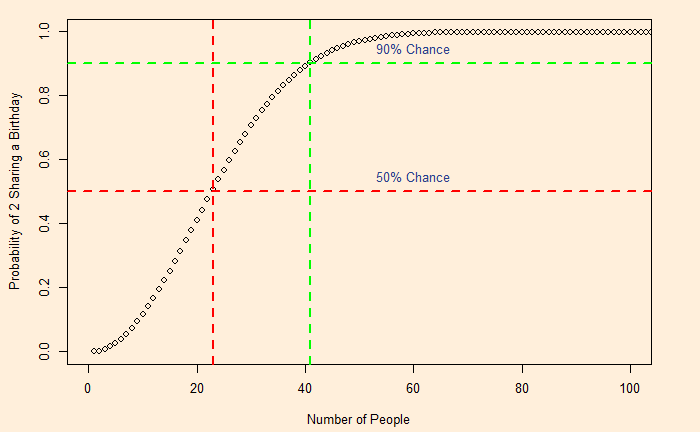
Guess Which outcome is more likely if I flip a coin six times – HHHHHH or HTTHTH?
Now, a slightly different one: assume a gambler gets 1 dollar for every head and loses 1 for the tail on a coin-tossing game; which of the two outcomes can shock you at the end of the sixth round of play – 6 dollars or 0 dollars?
These two problems have few things in common other than the fact that both are coin games. Let’s understand them quantitatively.
One Prize or Multiple Prizes?
The first problem is getting a specific sequence, i.e. HHHHHH or HTTHTH. The probability of getting any of the two is the same, which is (1/2) multiplied six times (0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.0156). In other words, both outcomes have the same chance of about 1%!
In the second problem, the sequence doesn’t matter, but getting (in some order) six heads or three. The second problem needs a new technique called a Bernoulli or binomial trial. In the mathematical form,
the probability of s successes in n rounds is
nCs x ps x q(n-s)
- nCs, The number of combinations of n things, taken s at a time or [n!/s!(n-s)!]
- p = probability of success in an individual trial
- q = probability of failure in an individual trial (= 1 – p)
That “!” mark in the formula means factorial. For example, 4! (four factorial) means 4 x3 x 2 x1; 5! = 5 x 4 x 3 x 2 x 1 etc
Binomial Distribution
Chance for 3 heads out of 6 (which means 0 dollars in the end!)
6C3 x (1/2)3 x (1/2)(6-3) = (6 x 5 x 4 x 3 x 2 x 1)/(3 x 2 x 1 x 3 x 2 x1) x 0.0156 = 0.3125
31% chance of losing all money
Chance for 6 heads out of 6 (6 dollars in the end!)
6C6 x (1/2)6 x (1/2)(6-6) = (6 x 5 x 3 x 2 x 1)/(6 x 5 x 3 x 2 x 1) x 0.0156 = 0.0156.
1% chance of winning all.
Note that the binomial coefficient, 6C3 or 6C6, made the difference between the first problem and the second.
Binomial Probability Calculator
Factorial Calculator
What to Expect from Tossing of Coins Read More »