The Poisson Cars and Binomial Hires

A car hire firm typically receives an average of 3 hiring requests per day. What is the probability it gets at most two hiring requests for exactly 3 days a week?

The first part of the problem (getting at most 2 requests in a day) can be solved using the Poisson probability model. It involves a random variable, X, and it takes positive values. All we know is an expected value (average value), lambda. The probability is expressed as:

$P(X = s) = \frac{e^{-\lambda}\lambda^s}{s!}$

Now, substitute lambda = 3 and s for at most 2 requests, i.e., the chance of 0 requests + 1 request + 2 requests.

$P(X \le 2) = \frac{e^{-3} 3^2}{2!} + \frac{e^{-3} 3^1}{1!} + \frac{e^{-3} 3^0}{0!} \\ \\ = \frac{9}{2}e^{-3} + 3e^{-3} + e^{-3} = 0.423$

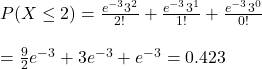
This can be easily estimated using the R code:

ppois(2, 3, lower.tail = TRUE)

This is the daily probability for at most 2 car hire requests. For estimating the probability of 3 exact such days in a week, we use the binomial model.

$P(X = 3) = _3C_7 * p^3 (1-p)^{7-3} \\ \\ P(X = 3) = _3C_7 * 0.423^3 (1-0.423)^{4} = 0.294$

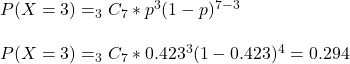
Or the R code.

dbinom(3, 7, prob = ppois(2, 3, lower.tail = TRUE))

Related Posts