The Lost Diamond of Bayes

Here is a problem that combines combinations with Bayes’s rule. A card is lost from the 52-card deck. Two cards are drawn from the deck and found to be both diamonds. What is the probability that the lost card is a diamond?

Let’s write down Bayes’ equation first.

P(L_D|2_D) = \frac{P(2_D|L_D)*P(L_D)}{P(2_D|L_D)*P(L_D) + P(2_D|L_{nD})*P(L_{nD})}

P(LD|2D) = The probability that the lost card is a diamond, given two diamonds are drawn.
P(2D|LD) = The probability of drawing two diamonds if the lost card is a diamond
P(LD) = The probability of losing a diamond.
P(2D|LnD) = The probability of drawing two diamonds if the lost card is not a diamond
P(LnD) = The probability of losing a card other than a diamond.

Evaluating each term,
As there are 13 diamonds in a pack of 52 cards, P(LD) is 13 in 52 (13/52 = 1/4), and P(LnD) is 52-13 in 52 (3/4).
P(2D|LD), or the probability of drawing two diamonds from a deck with a missing diamond, is 12C2 / 51C2 = 12 x 11 / (51 x 50).
P(2D|LnD), or the probability of drawing two diamonds from a deck with a missing non-diamond, is 13C2 / 51C2 = 13 x 12 / (51 x 50).

\\ P(L_D|2_D) = \frac{\frac{12*11}{51*50}*\frac{1}{4}}{\frac{12*11}{51*50}*\frac{1}{4} + \frac{13*12}{51*50}*\frac{3}{4}} \\ \\ \frac{12*11*(1/4)}{12*11*(1/4) + 13*12*(3/4)} = \frac{11}{50}

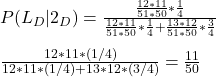
P(LD|2D) = 11/50 = 22%

Related Posts