Becky loves running 100-meter races. The run timing for girls her age follows a normal distribution with a mean of 15 seconds and a standard deviation of 1s. The cut-off time to get into the school team is 13.5 seconds. If Becky is on the school running team in 100 meters, what is the probability that she runs below 13 seconds?
Without any other information, we can use the given probability distribution to determine the chance of Becky running under 13 seconds.
pnormGC(13,region="below", mean=15,sd=1., graph=TRUE) 
Since we know she is in the school team, we can update the probability as per Bayes’ theorem. Let’s use the general formula of Bayes’ theorem here:
![]()
The first term in the numerator, P(T|13) = 1 (the probability of someone in the team with a cut-off of 13.5 s, given her timing is less than 13s). We already know the second term, P(13), 0.0228.
The denominator, P(T), is the probability of getting on the team, which is nothing but the chance of running under 13.5 seconds. That is,
pnormGC(13.5,region="below", mean=15,sd=1.,graph=TRUE)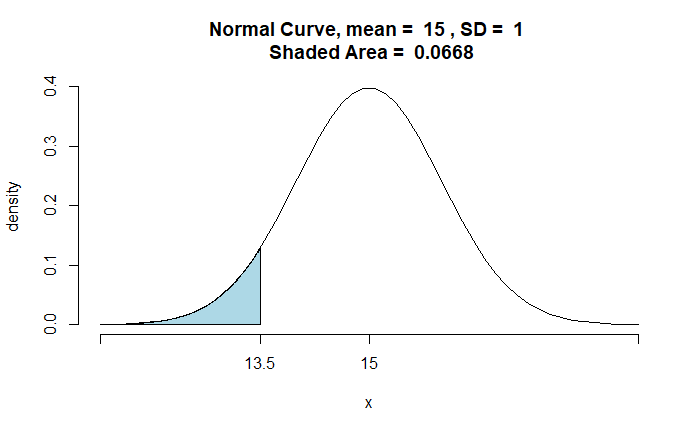
Substituting P(T) = 0.0668 in the Bayes equation,
P(13|T) = 0.0228/0.0668 = 0.34 or 34%

