We have seen the definitions. We will see their applications in diagnosis. As we have seen, both Sensitivity and Specificity are probabilities, and the diagnostic process’s job is to bring certainty to the presence of a disease from the data. And the tool we use is Bayes’ theorem. So let’s get started.
We tailor the Bayes’ theorem for our screening test. First, the chance of being infected after the person was diagnosed with a positive test. Epidemiologists call it positive predictive value or, in our language, the posterior probability.
Positive Predictive Value (PPV)
![]()
Looking at the equation carefully, we can see the following.
P(+|Inf) is the true positive or the sensitivity, and P(+|NoInf) is the false positive or (1 – Specificity). It leaves two unknown variables – P(Inf) and P(NoInf). P(Inf) is the prevalence of the disease in the community, and P(NoInf) is 1 – P(Inf).
![]()
And we’re done! Let’s apply the equation for a person who tested COVID-19 positive as part of a random sampling campaign in a city with a population of 100,000 and 100 ill people. The word random is a valuable description to remember; you will see the reason in a future post. Assume a sensitivity of 85% (yes, for your RT-PCR!) and a specificity of 98%.
Chance of Infection = 0.85 x 0.001 /(0.85 x 0.001 + 0.02 x 0.999) = 0.04. The instrument was of good quality, the health worker was skilled, and the system was honest (three deadly assumptions to make), yet she had only a 4% chance of infection.
Negative Predictive Value (NPV)
Now, quickly jump to the opposite: what is the chance someone who got tested negative, escapes the diagnostic web of the community?
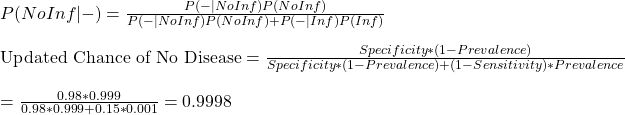
There is a 99.98% certainty of no illness or a 0.02% chance of accidentally escaping the realm of the health protocol.
What These Mean
In the first example (PPV), a 4% chance of infection means relief to the person eventually, but there is a pain to do the mandatory ‘insolation’ as the system treats her as an infected.
The second one (NPV) is the opposite; for the individual, 0.02% is low; therefore, a test with medium sensitivity is quite acceptable. For the system, which wants to trace and isolate every single infected person, this means, that for every 10,000 people sampled randomly, there is a chance to send out two infected individuals into the society.
We have made a set of assumptions regarding sensitivity, specificity and prevalence. And the output is related to those. We will discuss the reasons behind these assumptions, the cost-risk-value tradeoffs, and the tricks to manage traps of diagnostics. But next time. Ciao.
Bayes’ rule in diagnosis: PubMed
False Negative Tests: Interactive graph NEJM

