Bayesian Snow Flakes

Alice says there was snowfall last night. Becky says Alice lies 5 out of 6 times. Carol checked the previous day’s weather prediction and said the probability of snow was 1/8. What is the probability that there was snow?

We will use Bayes’ theorem to get the answer:

P(SN|AS) – Probability that it snowed, given Alice said so.
P(AS|SN) – Probability that Alice said snowed, given there was snow.
P(SN) – Prior probability of having snow.
P(AS|NS) – Probability that Alice said snowed, given there was no snow.
P(NS) – Prior probability of having no snow.

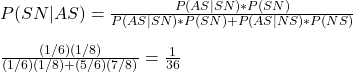
$\\ P(SN|AS) = \frac{P(AS|SN)*P(SN)}{P(AS|SN)*P(SN) + P(AS|NS)*P(NS)} \\ \\ \frac{(1/6)(1/8)}{(1/6)(1/8) + (5/6)(7/8)} = \frac{1}{36}$

1/36

Related Posts