I guess you remember the story of Sophie that we encountered at the start of our journey with the equation of life. She has tested positive during a cancer screening but found that the probability of the illness was about 12% after applying Bayes’ principles. There was nothing faulty about the test method, which was pretty accurate, at 95% sensitivity and 90% specificity. Now, how many independent tests does she need to undertake to confirm her illness at 90% probability?
Assume that her second test was positive: The probability for Sophie to have cancer, given that the second test is also positive,
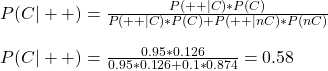
The updated probability has become 56% (note we have used 12.6%, which is the posterior of the first examination, as the prior and not the original 1.5%). Applying the equation one more time for a positive (third by now) test, you get
![]()
So the answer is three tests to get a high level of confidence.
You may recall that the prior probability used in the beginning was 1.5%, based on what she found in the American Cancer Society publications. What would have happened if she did not have that information? She still needs a prior. Let’s use 0.1% instead. Let’s work on the math, and you will find that about 89% probability can reach in the fourth test, provided all are positive. Therefore, an accurate prior is not that crucial as long as you follow up with more data collection, which is the power of the Bayesian approach.

