Suppose Ana wants to participate in a park run bingo – a version of what is known as stop-watch bingo – how many weekends is she expected to run to tick off the whole card?
In a stopwatch bingo, one tick off on the card, the digits (00-59), the seconds that show up on the watch. So for a weekly park run, it could be the seconds of the final timing recorded by the organiser. Notice if you take down timings from your watch, it becomes challenging to maintain randomness.

If you apply the formulation that we did in the earlier post, you get,
![]()
nn <- 60
run.sum <- rep(0, nn)
run.sum[1] <- 1.0
for(i in 2:nn){
current = nn/(nn - i +1)
run.sum[i] <- run.sum[i-1] + current
}
run.sum[nn]The answer is 281.
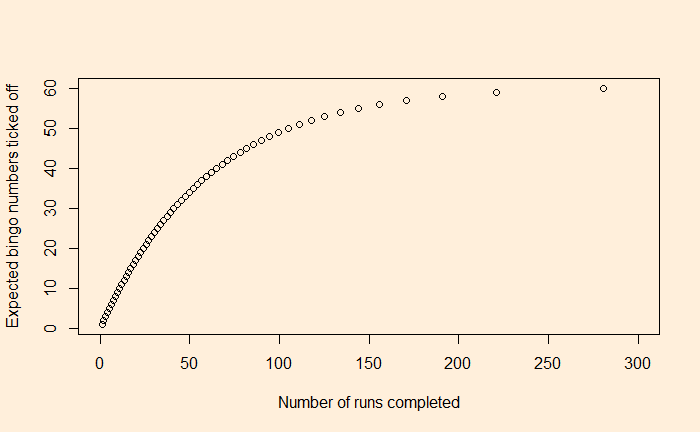
You can see from the graph that by about 50 runs, you could be getting close to 40 unique numbers; it then becomes difficult to avoid duplications.
The Coupon Collector’s Problem: Stand-up Maths
Coupon collector’s problem: Wiki

