Imagine that a person wants to collect coupons that come along with a product. Each product pack can contain one of the ten types of coupons, and her goal is to accumulate all of them. The question is: how many packets does she need to open to get all ten coupons?
Remember the post on expected waiting time? It says: if something has a probability p to occur, the amount of time you wait 1/p. It is the expected waiting time. So, start our problem in steps.
The probability of getting a new coupon from the first purchase is 10/10 = 1. The expected time or the number of packets to open is 1/1 = 1, which is not surprising. Note that it is a problem with replacement, i.e., the same type of coupon can come again. What is the probability of getting a new card the next time? It’s given by dividing the number of ‘not-yet-collected’ coupons / by the total number of coupons = 9/10. Naturally, the expected time gets longer = 10/9. Finally, when you got everything but the last, it requires 10/1 or ten purchases for the elusive one!
The total time required is the time to get the first coupon + the additional time for the second + third + … 10. It is 1 + 10/9 + 10/8 + 10/7 + 10/6 + 10/5 + 10/4 + 10/3 + 10/2 + 10/1 = 10 (1/10 + 1/9 + …. 1). Rearranging this will make it familiar: 10 (1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + 1/10).
In general, for N coupons, it becomes N x (1 + 1/2 + …. 1/N) = N x HN. And HN is the Nth Harmonic number. From the wiki, the approximation for the sum equals,
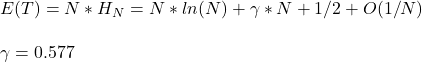
So, for the 10-coupon problem. she may be purchasing, on average, 29 packs of the product!
Coupon collector’s problem: Wiki

