Remember when we discussed the application of Bayes’ theorem to quantify the predictive values of medical tests? It gives the probability that a person has a (rare) disease, given she is tested positive. Today, we verify the solution using a simple R code by sampling a million people!
Using the familiar notations, we write down Bayes’ formula.
![]()
Let’s assign probabilities to each of the parameters.
1) The test shows positive 90% of the time on patients with the disease (high sensitivity); P(+|D)
2) The test shows negative 95% of the time on healthy patients (high specificity); P(-|noD)
3) The disease is present in 1% of the community (low prevalence ) P(D)
Note that specificity = P(-|noD), whereas what we want is P(+|NoD), which is 1 – P(-|noD). Substituting all values,
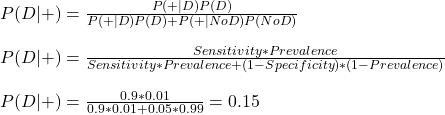
Let’s develop a code that simulates the testing of a million people.
Step 1: A million people, with 1% (random) having the disease. 1 = disease, 0 = no disease.
disease <- sample(c(0,1), size=1e6, replace=TRUE, prob=c(0.99,0.01))Step 2: Create an empty vector with a million slots.
test <- rep(NA, 1e6)Step 3: Fill the disease columns (disease = 1) with random assignment of test results; 90% with 1 and 10% with 0.
Fill the nondisease columns (disease = 0) with random assignment of test results; 95% with 0 and 0.05% with 1.
test[disease==1] <- sample(c(0,1), size=sum(disease==1), replace=TRUE, prob=c(0.1, 0.9))
test[disease==0] <- sample(c(0,1), size=sum(disease==0), replace=TRUE, prob=c(0.95,0.05))Now estimate the average number of people with disease = 1 AND test = 1.
mean(disease[test==1]==1)Putting everything together,
disease <- sample(c(0,1), size=1e6, replace=TRUE, prob=c(0.99,0.01))
test <- rep(NA, 1e6)
test[disease==1] <- sample(c(0,1), size=sum(disease==1), replace=TRUE, prob=c(0.1, 0.9))
test[disease==0] <- sample(c(0,1), size=sum(disease==0), replace=TRUE, prob=c(0.95,0.05))
mean(disease[test==1]==1)
