Whose Fault was It?

A company gets their tools from three factories, 10% from F1, 50% from F2 and 40% from F3. The fault rates of the three factories are 2.5%, 1.5% and 1%, respectively. If the company finds one of the tools defective, from which factory is it likely?

Let’s write down things in the proper format and test the probabilities, one by one. Let P(F1|D) be the probability that the tool came from F1 given the information (that it is faulty), P(D|F1), the fault rate of F1 and P(F1) is the prior chance of F1 in the company.

$\\ P(F1|D) = \frac{P(D|F1)*P(F1)}{P(D|F1)*P(F1) + P(D|F2)*P(F2) + P(D|F3)*P(F3)} \\ \\ P(F2|D) = \frac{P(D|F2)*P(F2)}{P(D|F1)*P(F1) + P(D|F2)*P(F2) + P(D|F3)*P(F3)} \\ \\ P(F3|D) = \frac{P(D|F3)*P(F3)}{P(D|F1)*P(F1) + P(D|F2)*P(F2) + P(D|F3)*P(F3)}$

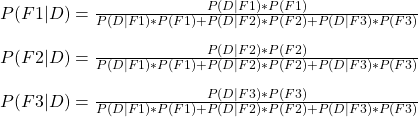
I guess you already know that I applied Bayes’ theorem to each factory. Now, add numbers and solve.

$\\ P(F1|D) = \frac{0.025*0.1}{0.025*0.1 + 0.015*0.5 + 0.01*0.4} = \frac{0.0025}{0.014} = 0.18\\ \\ P(F2|D) = \frac{0.015*0.5}{0.025*0.1 + 0.015*0.5 + 0.01*0.4} = \frac{0.0075}{0.014} = 0.54\\ \\ P(F3|D) = \frac{0.01*0.4}{0.025*0.1 + 0.015*0.5 + 0.01*0.4} = \frac{0.004}{0.014} = 0.29$

The tool is more likely to have come from F2.

Related Posts