What Monty Must Do

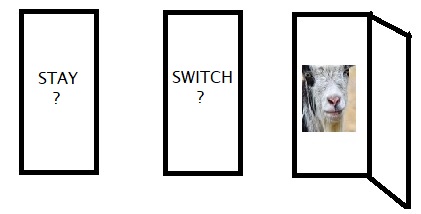
This one is about what Mr Monty shouldn’t do in the game show! The discussion on the “ideal” Monty Hall problem is available in a different post. Nonetheless, a quick proof is here. Suppose the player chose door 1 and Monty opened door 2, the probability of the car behind door 1 given Monty opened door 2 is P(C1|D2). Applying the Bayes’ formula,

\\ P(C1|D2) = \frac{P(D2|C1)*P(C1)}{P(D2|C1)*P(C1) + P(D2|C2)*P(C2) + P(D2|C3)*P(C3)} \\ \\ P(C1|D2) = \frac{(1/2)*(1/3)}{(1/2)*(1/3) + 0*(1/3) + (1*(1/3))} = \frac{1}{3} \\ \\ P(C3|D2) = 1 - 0 - P(C1|D2) = \frac{2}{3}

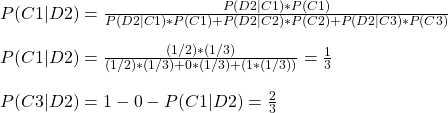
Explanation

The prior probabilities, P(C1), P(C3) and P(C3), are all equal at 1/3. P(D2|C1) = 1/2 because Monty can not open D1, and only D2 or D3 (one out of two) is available. P(D2|C2) = 0 since Monty can never open D2 if the car is behind the door 2. Since the car really exists behind one of those doors, P(C1) + P(C3) + P(C3) and P(C1|D2) + P(C2|D2) + P(C3|D2) are both unity.

The real-life Monty vs the perfect problem

The motivation for this post is when I read somewhere that Monty Hall did not always open the door in the game show. If that was true, then the TV show presented a different uncertainty than what should’ve been a calculated risk due to probability.

Related Posts