Vaccine Kinetics – What Chemist Sees

Let me start with a disclaimer: this is purely for demonstration purposes. The numbers used in the following analysis should not be viewed as an accurate description of the complex biological processes in the body.

In an earlier post explaining vaccination, I had mentioned the law of mass action. It is also called chemical kinetics. For a chemist, everything is a reaction, and solving kinetic equations are the way of understanding the world around her.

Equations of life

Molecules react to form products. Consider the following hypothetical reactions.

(1) $\begin{equation*} \begin{aligned} V\xrightarrow{\text{k1}}2V \\ \end{aligned} \end{equation*}$

(2) $\begin{equation*} \begin{aligned} P\xrightarrow{\text{k2}}A \\ \end{aligned} \end{equation*}$

(3) $\begin{equation*} \begin{aligned} V + C \xrightarrow{\text{k3}} cell death \\ \end{aligned} \end{equation*}$

(4) $\begin{equation*} \begin{aligned} A + V\xrightarrow{\text{k4}} precipitate \end{aligned} \end{equation*}$

^{V represents virus, A for antibody, C for cells and P for blood plasma.}

As per the law of mass action, the speed of a reaction is related to its rate constant and concentrations of ingredients. The four items above translate to a set of differential equations,

(5) $\begin{equation*} \begin{aligned} \frac{dC_V} {dt} = 2 k1 C_V - k3 C_V C_C - k4 C_A C_V \\ \end{aligned} \end{equation*}$

(6) $\begin{equation*} \begin{aligned} \frac{dC_A} {dt} = k2 - k4 C_A C_V \\ \end{aligned} \end{equation*}$

(7) $\begin{equation*} \begin{aligned} \frac{dC_C} {dt} = - k3 C_V C_C \\ \end{aligned} \end{equation*}$

What do these equations mean?

All three equations have a rate (speed) term on the left and a set of additions (production) and subtractions (consumption) on the right.
The speed of each reaction is related to the concentrations of the constituents.
If a reaction rate constant increases, the speed of the reaction increases.
The production rate of antibodies (from blood plasma) is assumed constant.

Let us solve these three differential equations simultaneously. I used the R package ‘deSolve’ to carry out that job.

Case 1: A person in a risky group and no vaccination

Used the following set of (arbitrary) numbers: k1 = 0.45, k2 = 0.05, k3 = 0.01, k4 = 0.01. Intial concentrations (time = 0) Ca = 0, Cc = 100, Cv = 1.

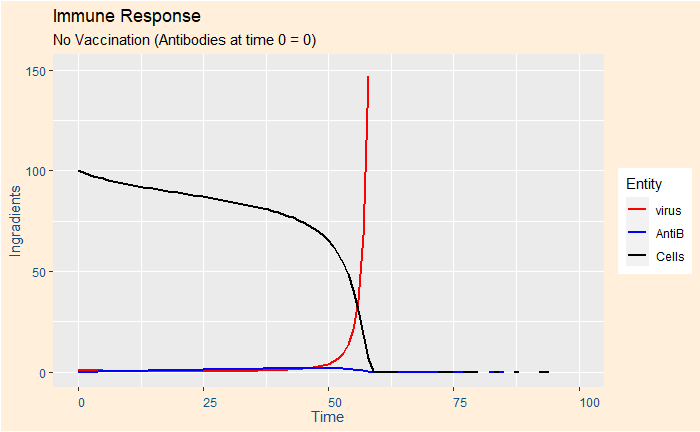
You can see that the person is in real danger as all her cells have been attacked by the virus that multiplied exponentially.

Case 2: A person with healthy antibody production and no vaccination

Now, use exactly the same input, but the antibody production rate constant k2 is 4 x: k1 = 0.45, k2 = 0.2, k3 = 0.01, k4 = 0.01.

The initial growth of the virus was curbed down pretty fast by the antibodies and the person survived.

Case 3: Risky group and vaccination

The parameters are the same as in case 1, but 5 units of antibodies are available at time zero (from vaccination).

Case 4: Risky group, vaccination, double viral load

Same as case 3, but the initial viral concentration doubled – from 1 to 2.

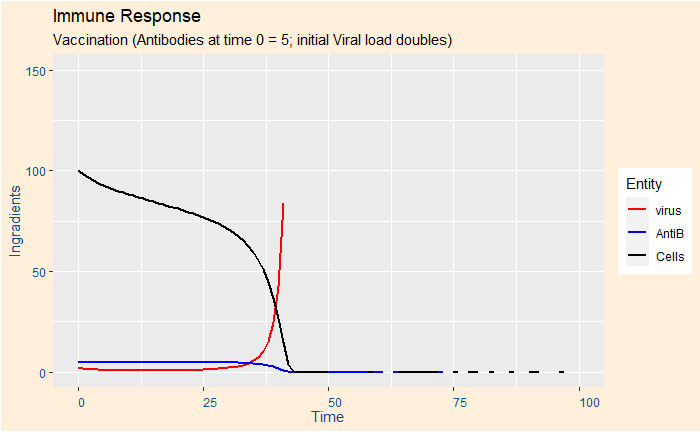
Case 5: Risky group, booster vaccination, double viral load

Same as case 4, but the antibodies from vaccination was double, or at ten units.

Case 6: No vaccination and double viral load

This case was created to show the speed at which the virus took control over the body. The parameters are exactly the same as case 1, but the initial virus load increased to 2 from 1.

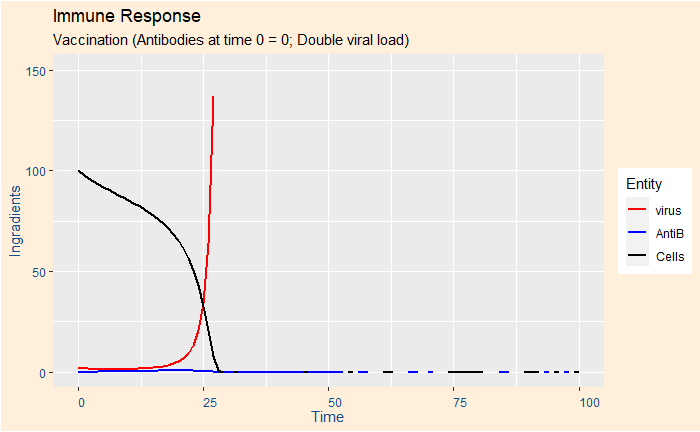
In summary

These are simplistic ways of picturing what dynamics are going on in our body once a virus comes in. Treatments (mathematical) like these can also expand our imagination to newer ways of managing the illness. Say, can we find a way to reduce the rate constant k1 (viral replication)? Antiviral drugs such as ‘molnupiravir’ are expected to do precisely this.

Mechanism of molnupiravir-induced SARS-CoV-2 mutagenesis: Nature