The CEO wants to know the annual budget requirements of 10 of her department heads. Each expects an average of $1 million. Each head decides to present not the average value but a value they are 90% confident they won’t exceed. If they assume their uncertainties are normally distributed, with a standard deviation of 0.1 and submit the figures, what should the CEO allocate for the whole firm?
Step 1: Budget request for a single department
Using the assumption of normal distribution, the budget that is expected to be at the 90 percentile (there is a 90% chance the amount will be within) is $1.13 million. Here is the representation.
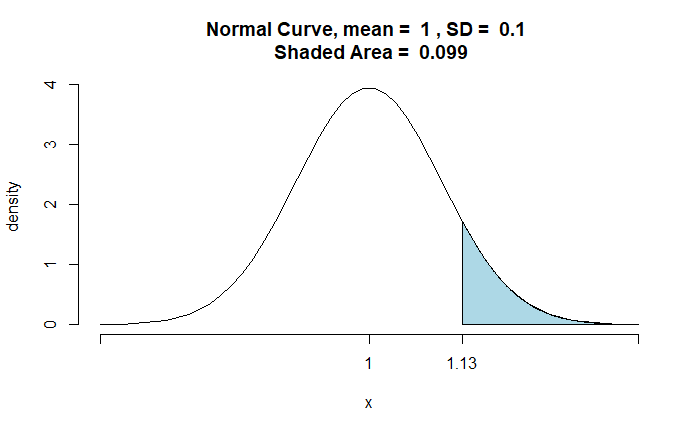
Step 2: Budget for the whole company
This is what each head would see. According to this, there are ten requests of $1.13 million or $11.3 million. The CEO uses this information and estimates that the firm’s annual budget has a 90% chance of not exceeding it.
The sum of two independentΒ random variables, X and Y, that areΒ normally distributed, Z = X + Y, is also normally distributed.
XβΌπ(πX,πX2)
πβΌπ(ππ,ππ2)
π=π+π βΌ π(ππ+ππ, ππ2+ππ2).
For ten distributions with similar mean and standard deviations, the sum becomes
Z βΌ π(10π, 10π2)
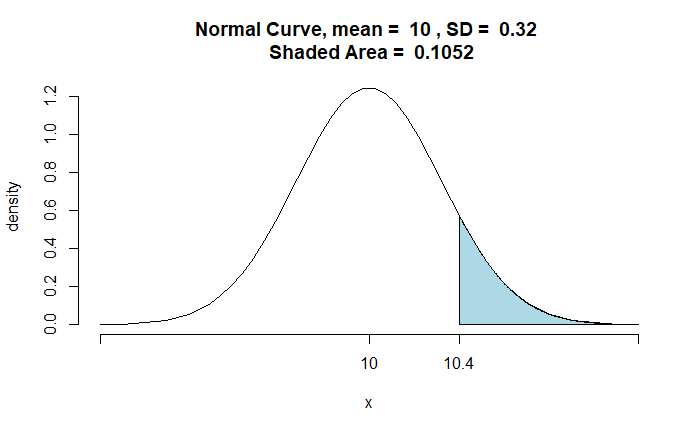
The CEO will be required to set aside $10.4 million to manage the company within budget at 90% confidence.
Reference
The Flaw of Averages: Sam L Savage
